The Michaelis-Menten equation is a fundamental concept in the field of enzyme kinetics and plays a crucial role in understanding the principles of enzymatic reactions. Developed by biochemists Leonor Michaelis and Maud Menten in 1913, this equation provides a quantitative description of how enzymes interact with substrates to catalyze chemical reactions.
Over the years, the Michaelis-Menten equation has become an indispensable tool in biochemical research, helping scientists investigate and characterize enzymatic reactions under various conditions. Its simplicity and applicability have made it a cornerstone in the study of enzyme kinetics, providing insights into enzyme-substrate interactions, reaction rates, and enzyme efficiency.
In this article, we will delve into the enigmatic world of the Michaelis-Menten equation and explore 17 intriguing facts that highlight its significance in the realm of biochemistry. So, buckle up and prepare to unravel the mysteries behind this essential equation!
Key Takeaways:
- The Michaelis-Menten Equation helps scientists understand how enzymes work and how fast they can make reactions happen. It’s like a secret code that unlocks the mysteries of biochemical processes!
- By using the Michaelis-Menten Equation, scientists can figure out how to make medicines work better and understand how chemicals interact in the body. It’s like a superhero tool for biochemists!
The Michaelis-Menten Equation is named after Leonor Michaelis and Maud Menten.
Leonor Michaelis and Maud Menten, two biochemists, developed this equation in 1913 to describe the rate of enzymatic reactions.
It is a cornerstone of enzyme kinetics.
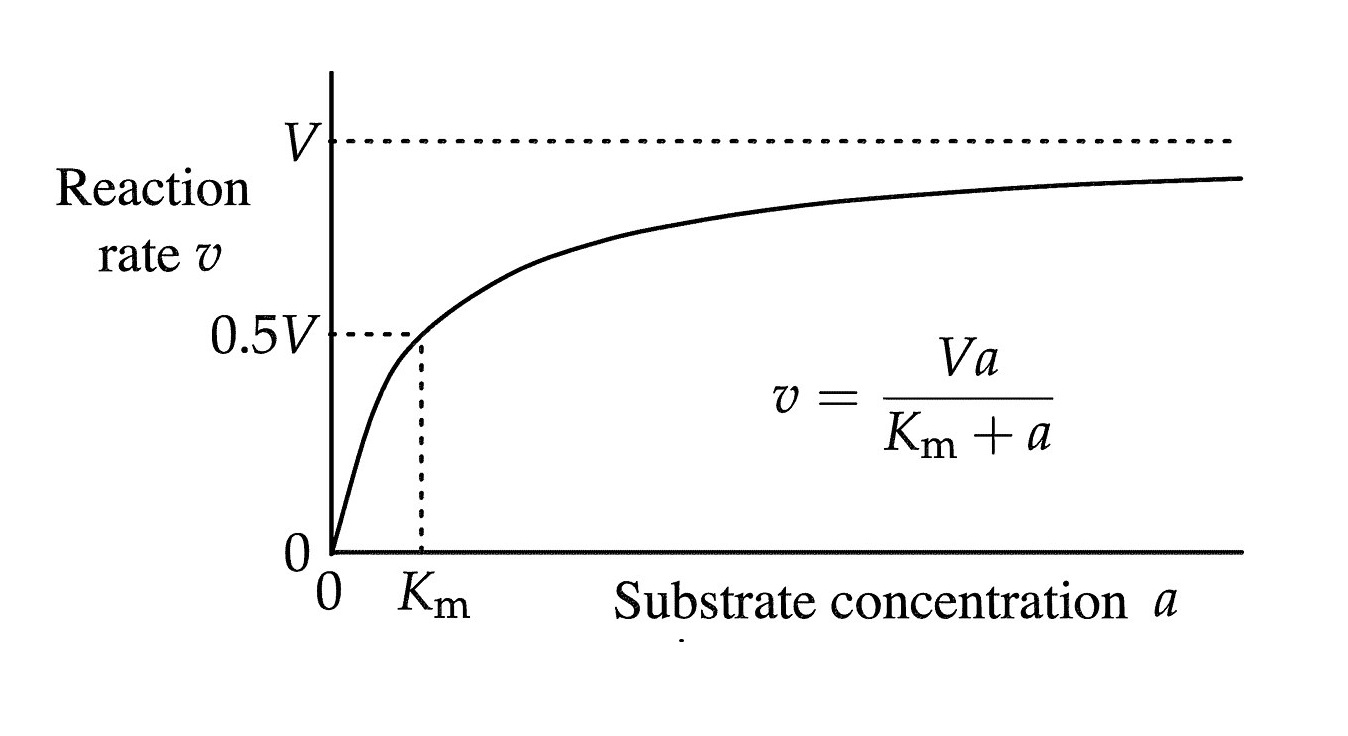
The Michaelis-Menten Equation provides insight into the relationship between enzyme concentration, substrate concentration, and reaction rate.
The equation is represented by
V = (Vmax * [S]) / (Km + [S]),
where V is the initial reaction velocity, Vmax is the maximum reaction velocity, [S] is the substrate concentration, and Km is the Michaelis constant.
The equation assumes a simple one-substrate enzyme reaction.
It does not account for enzymes with multiple substrates or complex reaction mechanisms.
The Michaelis constant (Km) is a measure of enzyme-substrate affinity.
A lower Km value indicates high affinity, while a higher value indicates lower affinity.
The Vmax represents the maximum rate of reaction.
It is achieved when the enzyme is saturated with the substrate.
The Michaelis-Menten Equation can be linearized using various methods.
Some popular linearization methods include Lineweaver-Burk plot, Eadie-Hofstee plot, and Hanes-Woolf plot.
The equation assumes steady-state conditions.
Steady-state conditions imply that the rate of formation of the enzyme-substrate complex equals the rate of its breakdown.
The Michaelis-Menten Equation is derived from an enzyme reaction mechanism known as the “M-M model.”
This model assumes that the enzyme-substrate complex is in rapid equilibrium with the free enzyme and substrate.
The equation provides valuable insights into enzyme kinetics.
It helps determine crucial parameters such as enzyme efficiency, catalytic power, and substrate specificity.
The Michaelis-Menten Equation is widely used in pharmacokinetics.
It helps determine drug concentration and dosage regimens to achieve optimal therapeutic effects.
The equation is applicable beyond enzymology.
It has found applications in diverse fields, including biochemistry, chemistry, and chemical engineering.
The Michaelis-Menten Equation assumes an initial rate approximation.
It measures the initial velocity of the reaction when the concentration of the product is negligible.
The equation assumes an idealized enzyme-substrate interaction.
It assumes that only the formation and breakdown of the enzyme-substrate complex are significant in the overall reaction.
The Michaelis-Menten Equation is not influenced by the enzyme concentration.
It only depends on the enzyme’s catalytic properties and the substrate concentration.
The equation provides a theoretical framework for enzyme inhibition studies.
It helps characterize competitive, non-competitive, and mixed types of inhibition.
The Michaelis-Menten Equation is a fundamental tool in the field of biochemistry.
Understanding enzymatic reactions and kinetics is essential for studying various biological processes.
Conclusion
Overall, the Michaelis-Menten equation is a fundamental concept in biochemistry and enzymology. It provides a mathematical framework for understanding enzyme kinetics and the relationship between substrate concentration and reaction rate. Through this equation, scientists have gained insight into various aspects of enzyme behavior, such as enzyme efficiency, maximum reaction rate, and substrate saturation.
Understanding the enigmatic facts about the Michaelis-Menten equation can greatly enhance one’s comprehension of enzymatic reactions and their regulation. These 17 intriguing facts have shed light on the complexities of enzyme kinetics and the underlying mechanisms that govern biological processes. By delving deeper into the Michaelis-Menten equation, researchers can continue to unravel the mysteries of enzymatic reactions and unlock new avenues for therapeutic interventions and applications.
FAQs
1. What is the Michaelis-Menten equation?
The Michaelis-Menten equation is a mathematical representation used to describe the rate of enzymatic reactions. It relates the reaction rate (V) to the substrate concentration (S) and essential enzyme parameters.
2. Why is the Michaelis-Menten equation important?
The equation is crucial because it provides insights into enzyme kinetics, including the maximum reaction rate (Vmax), the substrate concentration required for half-maximal reaction rate (Km), and the relationship between substrate concentration and reaction rate.
3. What does the Michaelis-Menten equation assume?
The equation assumes that the enzyme-substrate complex is in equilibrium, the rate of formation and breakdown of the complex is constant, and the reaction proceeds through a single-step mechanism.
4. Can the Michaelis-Menten equation be applied to all enzymes?
While the equation is widely applicable, it may not accurately describe enzymes that deviate from the assumptions, such as those with multiple substrates or complex reaction mechanisms.
5. How can the Michaelis-Menten equation be experimentally determined?
The equation’s parameters, Vmax and Km, can be determined by measuring the initial reaction rates at different substrate concentrations and plotting the data on a Lineweaver-Burk plot or using other enzyme kinetic analysis methods.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
