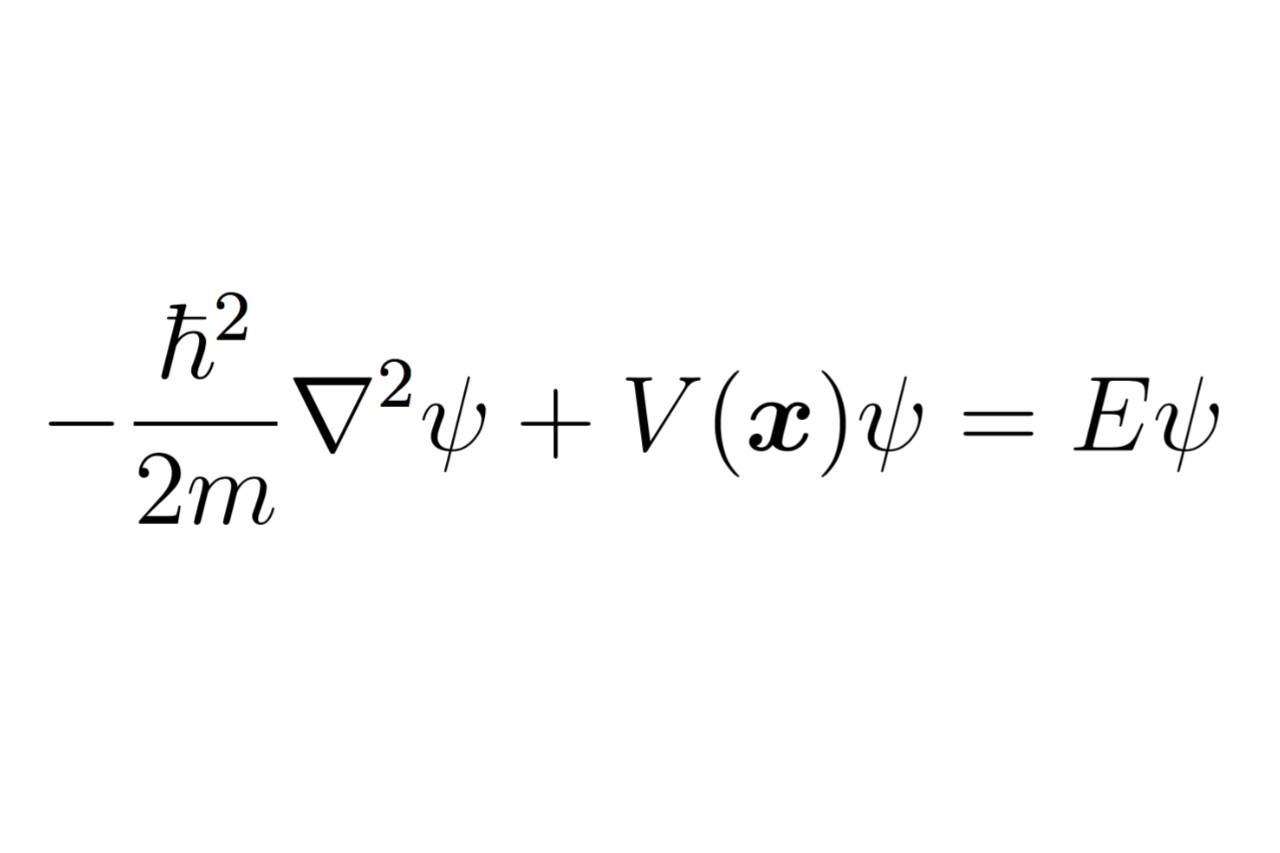
The Schrödinger equation is a fundamental concept in quantum mechanics that describes the behavior of particles at the subatomic level. Developed by the Austrian physicist Erwin Schrödinger in the 1920s, this equation revolutionized our understanding of the quantum world and laid the foundation for modern physics. Its enigmatic nature has intrigued scientists and philosophers alike, as it poses intriguing questions about the nature of reality and the strange phenomena that occur at the quantum level. In this article, we will delve into the mysteries and intricacies of the Schrödinger equation, exploring 14 fascinating facts that make it one of the most captivating concepts in the field of physics.
Key Takeaways:
- The Schrödinger Equation, developed in 1926, is a fundamental equation in quantum mechanics that describes the behavior of particles as both waves and particles, shaping our understanding of the quantum world.
- By solving the Schrödinger Equation, scientists can predict the probability distribution of finding particles, determine energy levels, and understand electron behavior, making it a crucial tool for unraveling the mysteries of the quantum world.
The Schrödinger Equation is a fundamental equation in quantum mechanics.
The Schrödinger Equation, named after the Austrian physicist Erwin Schrödinger, is the cornerstone of quantum mechanics. It describes the behavior of quantum systems, including particles such as electrons and atoms, by defining their wave functions.
It was developed in 1926.
Erwin Schrödinger introduced the Schrödinger Equation in 1926 as an alternative approach to describe the behavior of quantum systems. This groundbreaking equation revolutionized the field of quantum mechanics and provided a mathematical framework for studying the behavior of particles at the atomic and subatomic level.
The Schrödinger Equation is a partial differential equation.
The Schrödinger Equation is a complex partial differential equation that relates the time derivative of a particle’s wave function to its spatial derivatives. It captures the probabilistic nature of quantum mechanics by describing the evolution of the wave function over time.
The equation is a foundational principle of wave-particle duality.
The Schrödinger Equation reconciles the wave-particle duality of quantum systems. It allows particles to be described as both waves and particles, exhibiting characteristics of both entities depending on the experimental setup.
The equation predicts the probability distribution of finding a particle at a specific location.
By solving the Schrödinger Equation, scientists can determine the probability distribution of finding a particle in a particular region of space. This information is crucial for understanding the behavior of quantum systems and predicting experimental outcomes.
The Schrödinger Equation is time-dependent.
The Schrödinger Equation takes into account the evolution of quantum systems over time. It describes how the wave function of a particle changes as time progresses, allowing scientists to analyze and predict its behavior at different points in time.
The equation allows for the calculation of energy levels in quantum systems.
One of the key applications of the Schrödinger Equation is the determination of energy levels in quantum systems. By solving the equation, scientists can obtain the allowed energy states of a particle, providing insights into its stability and dynamics.
The Schrödinger Equation is a linear equation.
The linearity of the Schrödinger Equation allows for the superposition principle in quantum mechanics. It means that wave functions can be added together to form new wave functions, enabling the description of complex systems with multiple particles.
The equation cannot be solved analytically for most quantum systems.
While the Schrödinger Equation is relatively straightforward for simple systems, exact analytical solutions are often elusive for complex quantum systems. Researchers often rely on numerical methods or approximations to solve the equation and gain insights into the behavior of such systems.
The Schrödinger Equation is essential in understanding electron behavior in atoms.
The Schrödinger Equation is crucial for understanding the behavior of electrons in atoms. By solving the equation, scientists can determine the allowed energy levels and orbitals of electrons, providing a basis for understanding chemical bonding and the periodic table.
The equation shaped the development of quantum mechanics.
The introduction of the Schrödinger Equation played a pivotal role in the development of quantum mechanics as a field of study. It provided a unified framework for understanding the behavior of quantum systems and laid the foundation for further advancements and discoveries.
The equation is applicable to a wide range of physical systems.
The domain of the Schrödinger Equation extends beyond atoms and particles. It can be applied to various physical systems, including molecules, crystals, and even macroscopic systems under certain conditions, enabling scientists to study and explore the quantum nature of the world around us.
The Schrödinger Equation is a non-relativistic equation.
The Schrödinger Equation does not take into account relativistic effects, such as time dilation and length contraction. For particles moving at speeds close to the speed of light, relativistic quantum mechanics, such as the Dirac Equation, is required to accurately describe their behavior.
The Schrödinger Equation remains one of the most important equations in physics.
The Schrödinger Equation continues to be a cornerstone of modern physics. Its application extends across various fields, from quantum chemistry to solid-state physics, and it remains an essential theoretical tool for understanding and unraveling the mysteries of the quantum world.
Conclusion
The Schrödinger equation is a powerful and enigmatic equation in the field of quantum mechanics. It describes the behavior of quantum systems and has revolutionized our understanding of the microscopic world. Through its complex mathematical formulation, the Schrödinger equation provides insights into the wave-like nature of particles and allows for predictions of their probabilistic behavior.
From its origins in Erwin Schrödinger’s groundbreaking work, the equation has continued to shape the field of quantum mechanics and has been instrumental in the development of new technologies such as quantum computing. Its mathematical elegance and ability to accurately describe the behavior of particles in the quantum realm have made it a cornerstone of modern physics.
As we delve further into the mysteries of the quantum world, the Schrödinger equation will undoubtedly continue to play a vital role in unraveling its secrets and pushing the boundaries of our understanding.
FAQs
1. What is the Schrödinger equation?
The Schrödinger equation is a fundamental equation in quantum mechanics that describes the behavior of quantum systems. It mathematically represents the wave-like properties of particles and allows for predictions of their probabilistic behavior.
2. Who developed the Schrödinger equation?
The Schrödinger equation was developed by Austrian physicist Erwin Schrödinger in 1925. His work was instrumental in the development of quantum mechanics and earned him the Nobel Prize in Physics in 1933.
3. What does the Schrödinger equation tell us about particles?
The Schrödinger equation provides insights into the wave-like nature of particles. It allows us to calculate the probabilities of finding particles in different states and locations within a quantum system.
4. How is the Schrödinger equation used in technology?
The Schrödinger equation has many practical applications in technology, particularly in the field of quantum computing. It provides the basis for understanding and manipulating quantum states, which are essential for the development of advanced computational systems.
5. Can the Schrödinger equation be solved for all quantum systems?
While the Schrödinger equation can be solved analytically for simple quantum systems, it becomes increasingly complex for more intricate systems. In many cases, numerical approximations and computational methods are used to solve the equation.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.


