The Steiner-Lehmus theorem is a captivating result in geometry that has intrigued mathematicians for centuries. This theorem, which revolves around the uniqueness of angle trisection, has sparked both fascination and debate within mathematical circles. Understanding the intricacies of this theorem requires delving into its historical context, exploring its significance, and unraveling its mathematical underpinnings. In this article, we will embark on a journey to uncover nine essential facts about the Steiner-Lehmus theorem, shedding light on its origins, implications, and applications. From its enigmatic origins to its modern-day relevance, the Steiner-Lehmus theorem continues to captivate the minds of mathematicians and geometry enthusiasts alike. Join us as we unravel the mysteries and unveil the beauty of this timeless mathematical gem.
Key Takeaways:
- The Steiner-Lehmus Theorem states that if a triangle has two congruent angle bisectors, then it is isosceles, impacting fields like architecture and computer graphics.
- Named after mathematicians Steiner and Lehmus, the theorem challenges students to think critically and continues to inspire curiosity and learning in geometry.
Steiner-Lehmus Theorem is a theorem in Euclidean geometry.
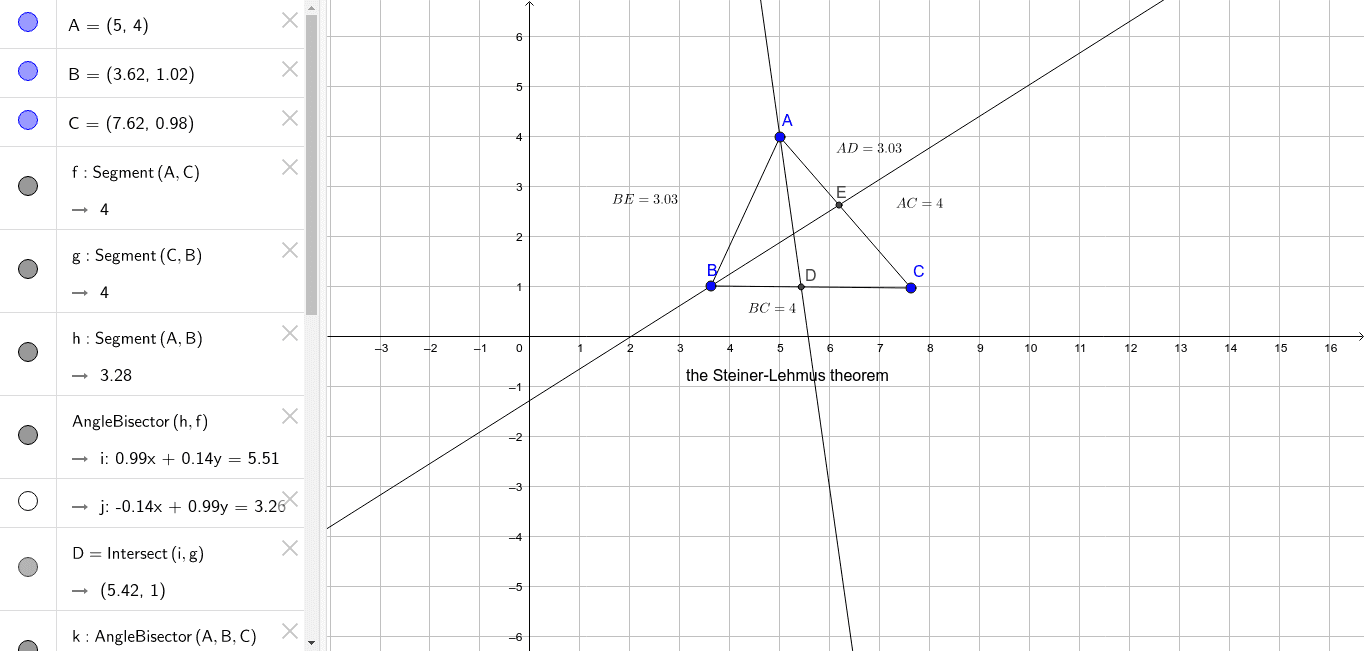
The Steiner-Lehmus Theorem is a fundamental result in Euclidean geometry that addresses the uniqueness of angle trisection. It states that if a triangle has two angle bisectors that are congruent, then the triangle is isosceles. This theorem has significant implications in geometry and trigonometry, making it a crucial concept for understanding the properties of triangles and angles.
The theorem is named after two mathematicians.
The theorem is named after the mathematicians Jakob Steiner and Carl Gustav Jacob Jacobi Lehmus, who independently discovered and proved the theorem in the 19th century. Their contributions to geometry and mathematics have left a lasting impact, and the theorem stands as a testament to their intellectual prowess.
It has practical applications in various fields.
The Steiner-Lehmus Theorem has practical applications in fields such as architecture, engineering, and computer graphics, where precise geometric constructions and calculations are essential. Understanding the properties of triangles and angle trisection is crucial for designing structures, creating visual simulations, and solving real-world problems that involve spatial relationships.
The theorem has historical significance.
The discovery and proof of the Steiner-Lehmus Theorem contributed to the advancement of geometric principles and mathematical reasoning. Its historical significance lies in its role in shaping the development of geometry as a discipline and its influence on subsequent mathematical discoveries.
The theorem challenges students to think critically.
Studying the Steiner-Lehmus Theorem encourages students to engage in critical thinking and problem-solving. It prompts them to explore the intricacies of triangle properties and angle relationships, fostering a deeper understanding of geometric concepts and mathematical reasoning.
The theorem is a subject of mathematical research and exploration.
Mathematicians and scholars continue to explore the implications and extensions of the Steiner-Lehmus Theorem, delving into related geometric phenomena and seeking connections to other areas of mathematics. This ongoing research contributes to the evolution of mathematical knowledge and the exploration of geometric principles.
The theorem exemplifies the elegance of mathematical proofs.
The elegant proof of the Steiner-Lehmus Theorem showcases the beauty and precision of mathematical reasoning. It serves as an example of the meticulous and logical approach that mathematicians employ to establish fundamental truths in geometry and other branches of mathematics.
The theorem fosters a deeper appreciation for geometric principles.
Studying the Steiner-Lehmus Theorem fosters an appreciation for the elegance and complexity of geometric principles. It encourages students and enthusiasts to explore the rich tapestry of geometric theorems and their interconnectedness, inspiring a deeper passion for mathematical exploration.
The theorem continues to inspire curiosity and learning.
The Steiner-Lehmus Theorem continues to captivate mathematicians, educators, and students, serving as a source of inspiration for further exploration and discovery in the realm of geometry and mathematical reasoning. Its enduring relevance and intellectual appeal make it a cornerstone of geometric knowledge and a catalyst for ongoing mathematical inquiry.
The Steiner-Lehmus Theorem stands as a testament to the enduring legacy of mathematical discovery and the timeless allure of geometric reasoning. Its impact reverberates through the annals of mathematical history, inspiring generations of mathematicians and learners to unravel the mysteries of triangles and angles.
Conclusion
In conclusion, the Steiner-Lehmus Theorem stands as a remarkable result in the realm of geometry, offering profound insights into the nature of isosceles triangles and the intricacies of angle trisection. Its historical significance, mathematical elegance, and enduring relevance in geometric studies make it a captivating subject for exploration. As we delve into the nine compelling facts about the Steiner-Lehmus Theorem, we gain a deeper appreciation for its impact on mathematical discourse and its enduring legacy in the field of geometry.
FAQs
What is the historical significance of the Steiner-Lehmus Theorem?The Steiner-Lehmus Theorem holds historical significance as one of the earliest results in geometry to address the challenge of angle trisection, a problem that has intrigued mathematicians for centuries. Its proof and implications have contributed to the evolution of geometric principles and the development of mathematical reasoning.
How does the Steiner-Lehmus Theorem relate to isosceles triangles?The theorem establishes a profound connection between the properties of isosceles triangles and the concept of angle trisection. By elucidating the unique characteristics of isosceles triangles in relation to angle trisection, the theorem sheds light on the intricate interplay between geometric elements.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
