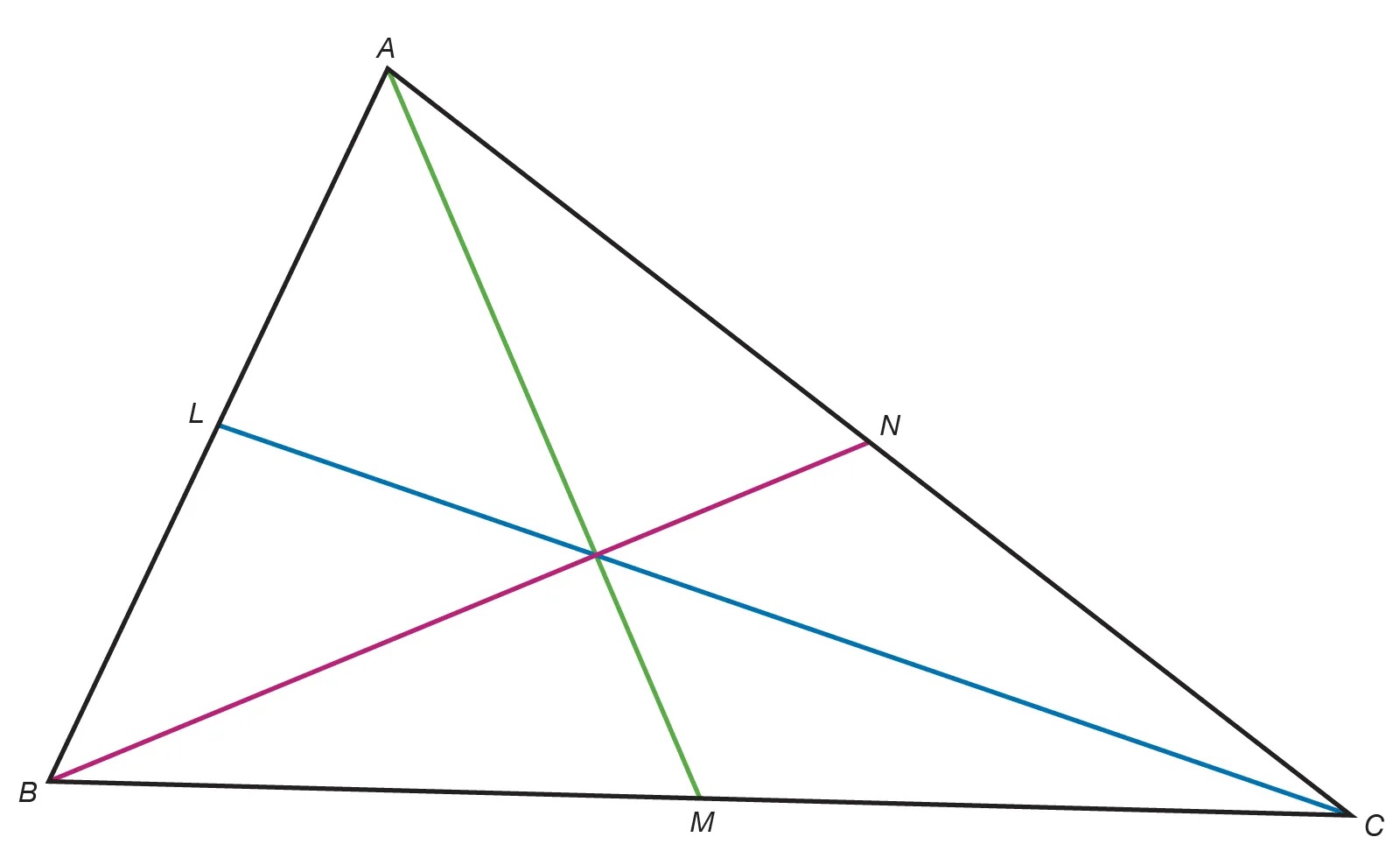
Ceva's Theorem is a fundamental concept in geometry that holds significant importance in various mathematical applications. Understanding this theorem can provide valuable insights into the relationships between different points within a triangle. Whether you're a student delving into the depths of geometry or a math enthusiast exploring the intricacies of mathematical theorems, delving into the details of Ceva's Theorem can be both enlightening and intellectually stimulating. In this article, we'll uncover nine essential facts about Ceva's Theorem, shedding light on its origins, applications, and significance in the realm of mathematics. So, let's embark on a journey to unravel the mysteries and beauty of Ceva's Theorem, gaining a deeper understanding of its principles and implications along the way.
Key Takeaways:
- Ceva’s Theorem, named after Giovanni Ceva, helps us understand how lines inside a triangle interact. It’s like a secret code that unlocks the mysteries of triangle geometry!
- By using Ceva’s Theorem, we can solve tricky triangle puzzles and become geometry masters. It’s like having a superpower for solving math problems!
Ceva's Theorem is Named After Giovanni Ceva
Giovanni Ceva, an Italian mathematician, is credited with formulating Ceva's Theorem in This theorem has since become a fundamental concept in geometry and is widely studied in mathematics and related fields.
Ceva's Theorem Relates to Triangles
Ceva's Theorem is a significant result in Euclidean geometry that deals with the relationships between various cevians within a triangle. It provides a crucial understanding of the interactions between the cevians and the sides of a triangle, offering valuable insights into the geometric properties of triangles.
It Involves Trigonometric Functions
Ceva's Theorem can be expressed using trigonometric functions, allowing for a deeper exploration of the connections between angles and sides within a triangle. This mathematical approach provides a comprehensive framework for analyzing the geometric configurations involved in the theorem.
Ceva's Theorem Demonstrates a Key Property of Triangles
Ceva's Theorem highlights an essential property of triangles, shedding light on the intricate interplay between the cevians and the sides of the triangle. By elucidating these relationships, the theorem enriches our understanding of the geometric principles governing triangles.
It Applies to Diverse Geometric Scenarios
Ceva's Theorem is not limited to specific types of triangles; rather, it applies universally across various geometric configurations. This versatility underscores the theorem's significance in geometry and its broad applicability in diverse problem-solving contexts.
Ceva's Theorem Facilitates Complex Geometric Calculations
By providing a systematic approach to analyzing the relationships within a triangle, Ceva's Theorem equips mathematicians and students with a powerful tool for tackling complex geometric calculations. Its practical utility extends to a wide array of mathematical scenarios.
It Offers Insights into Triangle Intersections
Ceva's Theorem delves into the intricate intersections within a triangle, unraveling the geometric intricacies that arise from the interactions between cevians and the sides of the triangle. This exploration enhances our comprehension of triangle geometry.
Ceva's Theorem Enhances Problem-Solving Skills
Studying Ceva's Theorem nurtures critical thinking and problem-solving abilities, fostering a deeper appreciation for the elegance and precision of geometric principles. This theorem serves as a cornerstone for honing mathematical reasoning skills.
It Holds Relevance Across Mathematical Disciplines
Ceva's Theorem transcends the boundaries of geometry and resonates across various mathematical disciplines, contributing to a holistic understanding of mathematical concepts and their interconnectedness.
Ceva's Theorem, named after Giovanni Ceva, is a pivotal concept in geometry that elucidates the intricate relationships within a triangle. This fundamental theorem, formulated in 1678, relates to the interactions between cevians and the sides of a triangle, offering valuable insights into the geometric properties of triangles. By incorporating trigonometric functions, Ceva's Theorem provides a comprehensive framework for analyzing the connections between angles and sides within a triangle. Its universal applicability across diverse geometric scenarios underscores its significance in geometry and problem-solving contexts. Furthermore, the theorem equips mathematicians and students with a powerful tool for tackling complex geometric calculations, enhancing their problem-solving skills and nurturing a deeper understanding of mathematical principles. Overall, Ceva's Theorem holds relevance across various mathematical disciplines, contributing to a holistic understanding of mathematical concepts and their interconnectedness.
Conclusion
In conclusion, Ceva's Theorem is a powerful and elegant tool in the field of geometry, offering a profound understanding of the relationships between cevians in a triangle. By delving into the nine essential facts about Ceva's Theorem, we have uncovered its significance in various geometric configurations and its applications in diverse mathematical problems. From its historical origins to its practical implications in modern mathematics, Ceva's Theorem continues to inspire and challenge mathematicians, educators, and enthusiasts alike. Embracing the beauty and complexity of this theorem opens up new avenues for exploration and problem-solving in the captivating realm of geometry.
FAQs
What is the historical significance of Ceva's Theorem?Ceva's Theorem holds historical significance as it is named after Giovanni Ceva, an Italian mathematician who introduced this fundamental geometric principle in 1678. This theorem has since become a cornerstone of triangle geometry, influencing various mathematical disciplines and inspiring further advancements in the field.
How is Ceva's Theorem applied in real-world scenarios?Ceva's Theorem finds practical applications in fields such as engineering, architecture, and computer graphics, where geometric principles are essential. By leveraging the insights provided by Ceva's Theorem, professionals can optimize structural designs, analyze spatial relationships, and solve complex geometric problems encountered in real-world applications.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
