8 Facts You Must Know About Desargues’ Theorem

Desargues' Theorem is a fundamental concept in projective geometry.

Desargues' Theorem is a fundamental concept in projective geometry, a branch of mathematics that deals with the properties of geometric figures that remain unchanged under projection. This theorem provides a powerful tool for understanding the relationships between different geometric elements and has wide-ranging applications in various fields of mathematics and beyond.

It is named after the French mathematician Girard Desargues.

Girard Desargues, a prominent figure in the development of projective geometry, is credited with formulating this theorem. His contributions to the field have had a lasting impact on the study of geometry and its applications in diverse areas, from architecture to computer graphics.

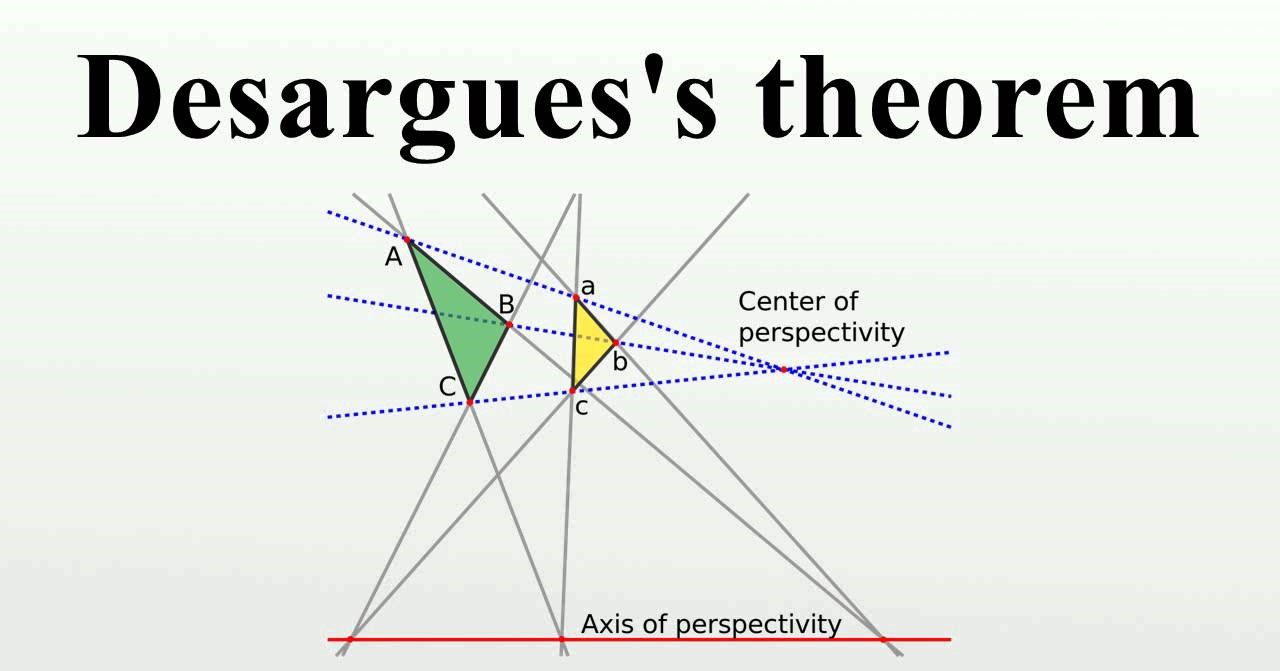
Desargues' Theorem states that if two triangles are perspective from a point, then they are perspective from a line.

This fundamental principle asserts that when two triangles are perspective from a point, they are also perspective from a line. This concept forms the basis for understanding the relationships between geometric shapes and has significant implications for the study of spatial relationships and transformations.

It is a key concept in the study of perspective and projective geometry.

Desargues' Theorem plays a crucial role in the study of perspective and projective geometry, providing valuable insights into the principles governing the visual representation of objects and scenes. Understanding this theorem is essential for artists, architects, and mathematicians seeking to comprehend the intricate interplay of lines, shapes, and spatial arrangements.

Desargues' Theorem is often used in computer graphics and 3D modeling.

The principles underlying Desargues' Theorem find practical applications in the realm of computer graphics and 3D modeling. By leveraging the insights offered by this theorem, professionals in these fields can create realistic and visually compelling representations of three-dimensional objects and environments.

It forms the basis for the concept of homography in computer vision.

Desargues' Theorem serves as the foundation for the concept of homography in computer vision, a field that focuses on enabling machines to interpret and understand visual data. The theorem's relevance in this context underscores its significance in modern technological advancements and its role in shaping the capabilities of computer vision systems.

Desargues' Theorem has connections to other branches of mathematics, such as linear algebra and projective spaces.

This theorem's far-reaching influence extends to other branches of mathematics, including linear algebra and projective spaces. Its connections to these areas highlight its interdisciplinary nature and its capacity to enrich various fields with its profound geometric insights.

It exemplifies the elegance and universality of mathematical principles.

Desargues' Theorem stands as a testament to the elegance and universality of mathematical principles, showcasing the beauty and applicability of geometric concepts in diverse contexts. Its enduring relevance underscores the enduring impact of mathematical discoveries on our understanding of the world around us.

Desargues' Theorem, named after the French mathematician Girard Desargues, is a fundamental concept in projective geometry. This theorem states that if two triangles are perspective from a point, then they are perspective from a line. It plays a crucial role in the study of perspective and projective geometry, offering valuable insights into the principles governing the visual representation of objects and scenes. Moreover, Desargues' Theorem has practical applications in computer graphics and 3D modeling, where it is utilized to create realistic representations of three-dimensional objects and environments. Additionally, this theorem forms the basis for the concept of homography in computer vision, highlighting its relevance in modern technological advancements. Furthermore, Desargues' Theorem has connections to other branches of mathematics, such as linear algebra and projective spaces, underscoring its interdisciplinary nature and its capacity to enrich various fields with its profound geometric insights. Overall, Desargues' Theorem exemplifies the elegance and universality of mathematical principles, showcasing the beauty and applicability of geometric concepts in diverse contexts.

Conclusion

Desargues' Theorem is a fundamental concept in projective geometry, offering profound insights into the relationships between points, lines, and planes. Its application extends beyond the realm of mathematics, finding relevance in various fields such as computer graphics, architecture, and art. Understanding the theorem's implications and applications can significantly enhance one's problem-solving skills and geometric intuition. By grasping the eight essential facts about Desargues' Theorem, individuals can gain a deeper appreciation for its significance and broaden their understanding of projective geometry.

FAQs

What is the significance of Desargues' Theorem?
Desargues' Theorem holds immense significance in projective geometry, providing a framework for understanding the relationships between geometric elements such as points, lines, and planes. Its applications extend to various fields, including computer graphics, architecture, and art.

How can Desargues' Theorem be applied in real-world scenarios?
Desargues' Theorem finds practical applications in fields such as architecture, computer graphics, and art, where understanding the relationships between points, lines, and planes is crucial. Its principles can be utilized to solve geometric problems and optimize spatial arrangements in practical design scenarios.