Pascal's Theorem, a fundamental concept in geometry, holds significant importance in the field of mathematical sciences. Named after the renowned French mathematician Blaise Pascal, this theorem elucidates the intricate relationships between points, lines, and conic sections. Understanding Pascal's Theorem is crucial for comprehending the underlying principles of projective geometry and its applications in various real-world scenarios.
In this article, we will delve into eight essential facts about Pascal's Theorem, unraveling its significance and shedding light on its practical implications. From its historical origins to its modern-day relevance in fields such as engineering, architecture, and computer graphics, Pascal's Theorem continues to inspire and inform mathematical thought and innovation. Join us as we embark on a journey through the captivating world of Pascal's Theorem, exploring its intricacies and unveiling the profound impact it has had on the realm of mathematical sciences.
Key Takeaways:
- Pascal’s Theorem, named after the brilliant mathematician Blaise Pascal, shows how points, lines, and shapes are connected in a cool way. It’s like a secret code for geometry!
- This theorem isn’t just for math class—it’s used in computer graphics, architecture, and engineering. It’s like a superhero, helping solve real-world problems with its math powers!
Pascal's Theorem is named after the French mathematician Blaise Pascal.
Blaise Pascal, a brilliant mathematician, and physicist, is renowned for his significant contributions to various fields, including mathematics, physics, and philosophy. His namesake theorem, Pascal's Theorem, has left an indelible mark on the world of mathematics.
The theorem is a fundamental concept in projective geometry.
Pascal's Theorem holds a pivotal position in projective geometry, a branch of mathematics that deals with the properties and invariants of geometric figures under projection. This theorem plays a crucial role in understanding the relationships between points, lines, and conic sections within a projective plane.
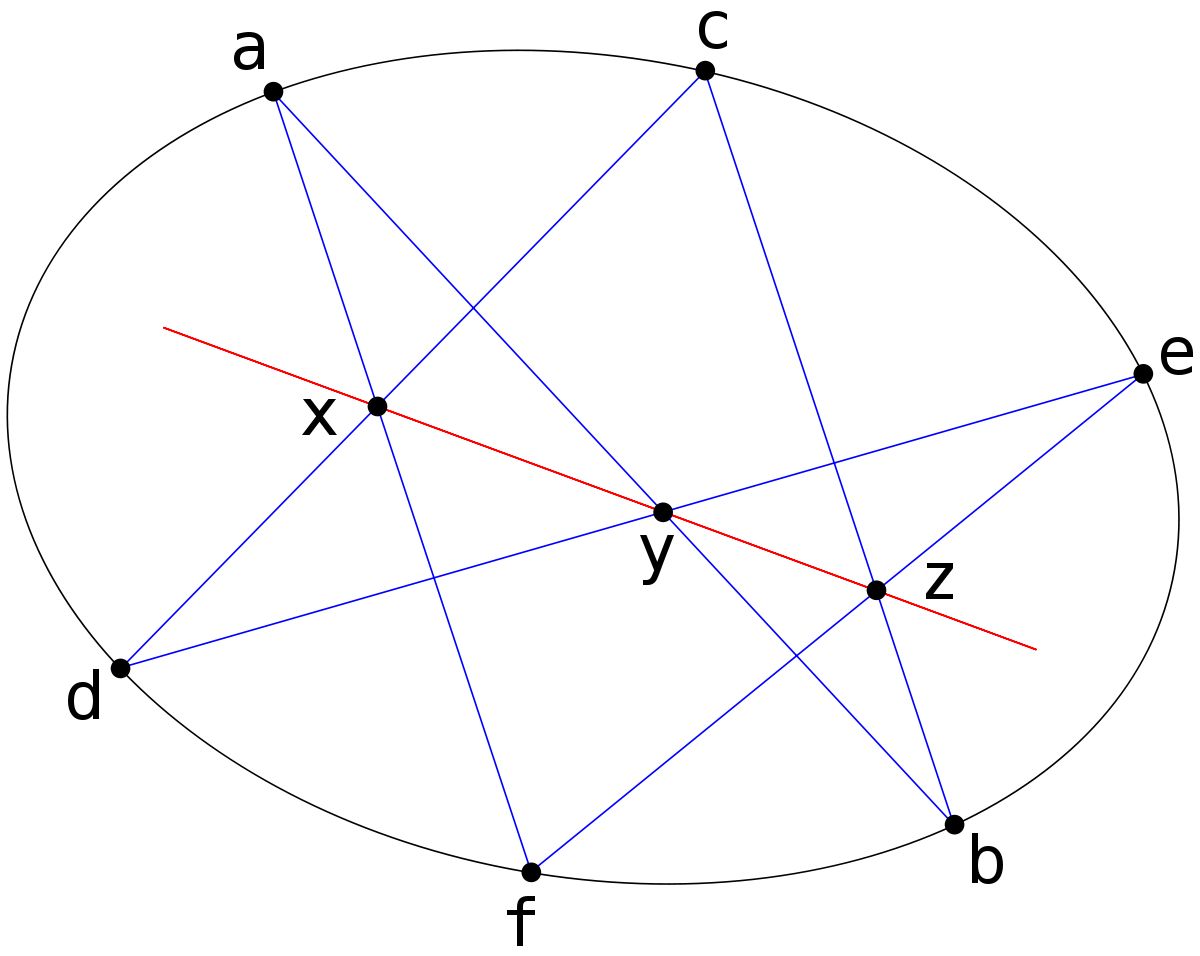
It states that if a hexagon is inscribed in a conic section, the intersections of opposite sides lie on a straight line.
Pascal's Theorem succinctly articulates the fascinating property of conic sections and their relationship to inscribed hexagons. This elegant statement encapsulates the essence of the theorem and its profound implications in geometry.
The theorem was first published in 1640 in Pascal's work "Essay pour les coniques."
Blaise Pascal introduced his groundbreaking theorem in his seminal work "Essay pour les coniques" in This publication marked a significant milestone in the history of mathematics, paving the way for further exploration and application of projective geometry principles.
Pascal's Theorem has diverse applications in various mathematical and real-world contexts.
From its foundational role in projective geometry to its applications in fields such as computer graphics, architecture, and engineering, Pascal's Theorem exhibits remarkable versatility and relevance across different domains.
The theorem provides a profound insight into the interconnectedness of geometric elements.
By elucidating the interconnected nature of points, lines, and conic sections, Pascal's Theorem offers a profound insight into the underlying unity and harmony within geometric configurations, enriching our understanding of spatial relationships.
It serves as a testament to the enduring legacy of mathematical principles.
Pascal's Theorem stands as a testament to the enduring legacy of mathematical principles, showcasing the timeless significance of geometric theorems and their enduring impact on the evolution of mathematical thought.
The theorem continues to inspire mathematicians and enthusiasts worldwide.
Pascal's Theorem continues to captivate the minds of mathematicians, educators, and enthusiasts worldwide, serving as a source of inspiration and intellectual fascination within the realm of geometry and mathematics.
Pascal's Theorem, named after the illustrious mathematician Blaise Pascal, holds a pivotal position in projective geometry, offering profound insights into the interconnectedness of geometric elements. With its diverse applications and enduring legacy, this theorem continues to inspire mathematicians and enthusiasts, underscoring its timeless significance within the realm of mathematics and geometry.
Conclusion
In conclusion, Pascal's Theorem is a remarkable result in projective geometry that has far-reaching applications in various fields, including engineering, computer graphics, and physics. Understanding the fundamental concepts and implications of this theorem is crucial for anyone delving into the realms of geometry and its practical applications. By grasping the significance of Pascal's Theorem and its underlying principles, one can gain valuable insights into the interconnectedness of geometric elements and harness its power to solve complex problems in diverse domains.
FAQs
What is the significance of Pascal's Theorem in real-world applications?
Pascal's Theorem has significant implications in various real-world applications, including engineering, computer graphics, and physics. It provides a powerful tool for solving complex geometric problems and understanding the interconnectedness of geometric elements in practical scenarios.
How can one apply Pascal's Theorem in problem-solving?
Pascal's Theorem can be applied in problem-solving by identifying and leveraging the interconnectedness of points and lines within a conic section. By recognizing the patterns and relationships outlined in the theorem, one can effectively solve intricate geometric problems and gain deeper insights into the underlying principles of projective geometry.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
