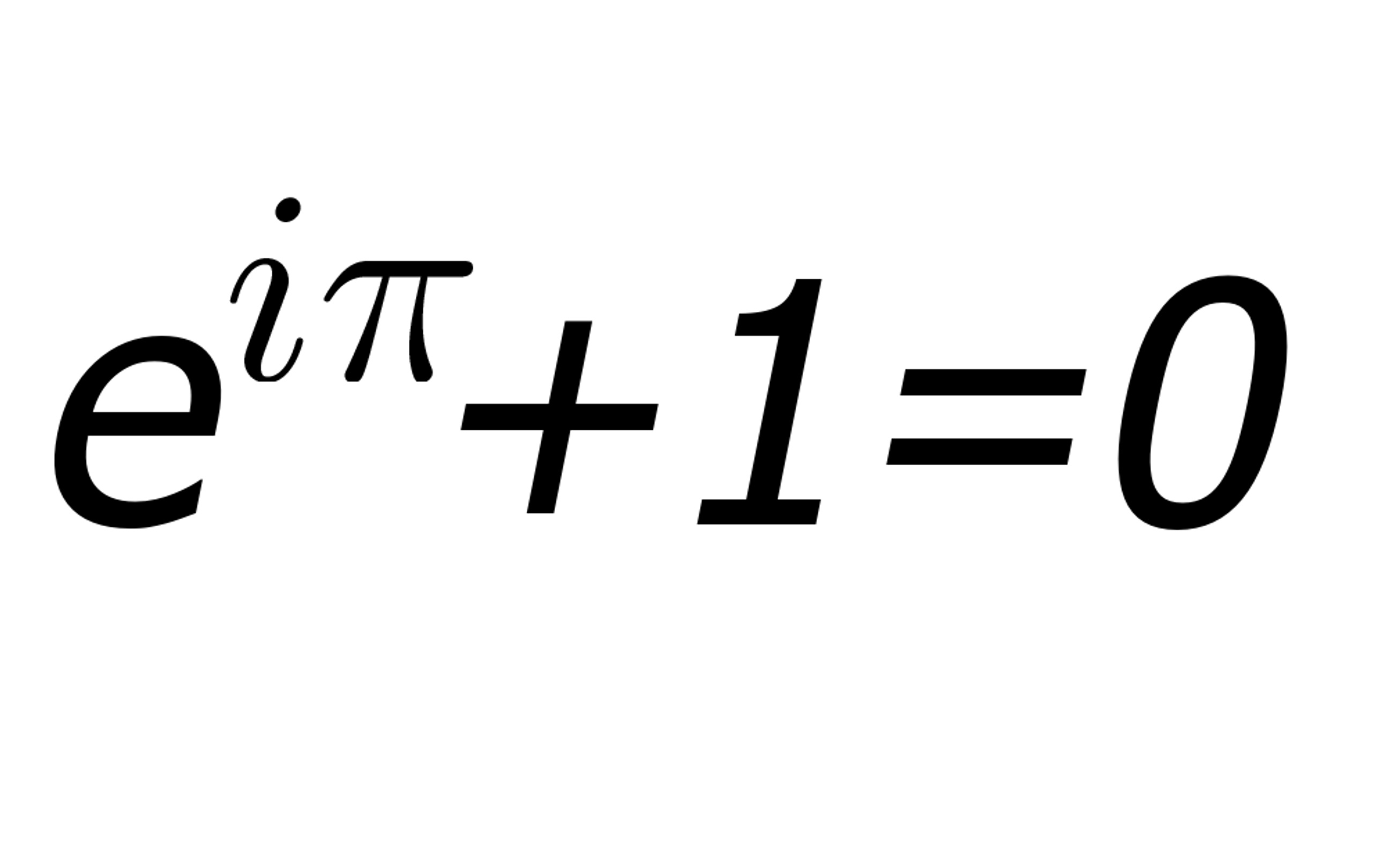
Euler's Identity is a remarkable mathematical equation that has captivated the minds of mathematicians, scientists, and enthusiasts for centuries. It elegantly combines five fundamental mathematical constants: 0, 1, ? (pi), e (Euler's number), and i (the imaginary unit). This seemingly simple equation, e^(i?) + 1 = 0, holds profound significance in various branches of mathematics, including complex analysis, number theory, and calculus.
Understanding Euler's Identity goes beyond mere mathematical curiosity; it unveils the interconnectedness of seemingly disparate mathematical concepts and serves as a testament to the elegance and beauty inherent in the language of mathematics. As we delve into the 12 facts about Euler's Identity, we will unravel the mystique surrounding this equation and gain a deeper appreciation for its significance in the mathematical world. So, let's embark on a journey to explore the intriguing facets of Euler's Identity and uncover the profound insights it offers.
Key Takeaways:
- Euler’s Identity unites fundamental constants like 0, 1, e, i, and ?, showcasing the interconnectedness of math concepts and defying intuition with unexpected connections.
- It embodies mathematical beauty, inspires philosophical reflection, and signifies unity within the mathematical universe, captivating the imagination and fueling ongoing exploration.
Euler's Identity is a Mathematical Marvel
Euler's Identity, denoted as e^(i?) + 1 = 0, is a remarkable equation that intertwines five fundamental mathematical constants: e (Euler's number), i (the imaginary unit), ? (pi), 1, and This equation elegantly connects complex numbers, exponential functions, and trigonometry, making it a cornerstone of mathematical beauty and elegance.
It Unites Fundamental Constants
Euler's Identity unites the most essential constants in mathematics: 0, 1, e, i, and ?, in a single, concise equation. This unification showcases the interconnectedness of seemingly disparate mathematical concepts, highlighting the profound elegance and symmetry within the mathematical universe.
It Defies Intuition
Euler's Identity defies intuition by demonstrating the unexpected relationship between exponential functions, complex numbers, and trigonometric functions. This unexpected connection challenges conventional mathematical reasoning, inviting mathematicians to explore the depths of this enigmatic relationship.
It Embodies Mathematical Beauty
Euler's Identity is celebrated for its unparalleled beauty and elegance in encapsulating complex mathematical concepts within a succinct and visually striking equation. Its aesthetic appeal has captivated mathematicians and enthusiasts alike, elevating it to an iconic status within the mathematical community.
It Inspires Philosophical Reflection
Euler's Identity transcends its mathematical significance, inspiring profound philosophical contemplation about the nature of reality, the interconnectedness of mathematical principles, and the enigmatic beauty inherent in the fabric of the universe. Its profound implications extend beyond mathematics, sparking introspection and wonder about the underlying structure of the cosmos.
It Fosters Mathematical Exploration
Euler's Identity serves as a catalyst for mathematical exploration, prompting researchers to delve into the intricate connections between different branches of mathematics. This exploration fuels the advancement of mathematical knowledge and fosters a deeper understanding of the underlying principles governing the mathematical world.
It Captivates the Imagination
Euler's Identity captivates the imagination with its enigmatic nature, inviting individuals to ponder the profound implications of its elegant formulation. Its ability to spark curiosity and wonder contributes to its enduring legacy as a source of inspiration for mathematicians and thinkers across the globe.
It Represents Mathematical Harmony
Euler's Identity symbolizes the harmonious coexistence of seemingly disparate mathematical elements, illustrating the symphonic unity that underlies the diverse branches of mathematics. This representation of harmony resonates deeply with mathematicians, serving as a testament to the interconnectedness and coherence of mathematical principles.
It Challenges Conventional Notions
Euler's Identity challenges conventional notions of mathematical separateness by revealing the intricate interplay between exponential, trigonometric, and complex functions. This challenge prompts a reevaluation of traditional mathematical boundaries, encouraging a more holistic and integrated approach to mathematical reasoning.
It Fuels Mathematical Inquiry
Euler's Identity fuels ongoing mathematical inquiry by instigating a quest for deeper comprehension of its underlying principles and implications. This perpetual quest for understanding propels mathematical research and contributes to the continuous evolution of mathematical knowledge.
It Evokes Mathematical Wonder
Euler's Identity evokes a sense of mathematical wonder, inspiring individuals to marvel at the profound interconnectedness and elegance embedded within the mathematical realm. Its ability to evoke wonder fosters a deep appreciation for the beauty and complexity of mathematical concepts.
It Signifies Mathematical Unity
Euler's Identity signifies the unity of mathematical principles, transcending disciplinary boundaries and emphasizing the interconnected nature of mathematical concepts. This representation of unity underscores the cohesive fabric of mathematics, highlighting the intrinsic coherence that permeates the diverse branches of mathematical study.
Euler's Identity stands as a testament to the profound elegance and interconnectedness inherent in the mathematical universe, captivating the imagination and inspiring a deeper appreciation for the beauty of mathematical concepts. Its enduring legacy continues to fuel mathematical exploration and philosophical contemplation, serving as a timeless symbol of unity and harmony within the realm of mathematics.
Conclusion
In conclusion, Euler's Identity stands as a remarkable testament to the interconnectedness of fundamental mathematical constants. It elegantly encapsulates the complex relationship between five pivotal numbers, offering profound insights into the nature of mathematics and its intrinsic beauty. Euler's Identity continues to captivate mathematicians, scientists, and enthusiasts alike, serving as a symbol of the inherent harmony and unity within the realm of mathematical principles.
FAQs
What makes Euler's Identity significant?Euler's Identity is significant due to its elegant representation of fundamental mathematical constants, including the base of the natural logarithm, the imaginary unit, and the transcendental number pi. This remarkable equation unites these essential elements in a concise and profound manner, showcasing the interconnectedness of seemingly disparate mathematical concepts.
How does Euler's Identity contribute to mathematical understanding?Euler's Identity contributes to mathematical understanding by providing a profound insight into the relationships between essential mathematical constants. By succinctly expressing the interplay between e, pi, and the imaginary unit, this identity offers a glimpse into the inherent harmony and unity within the realm of mathematical principles.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
