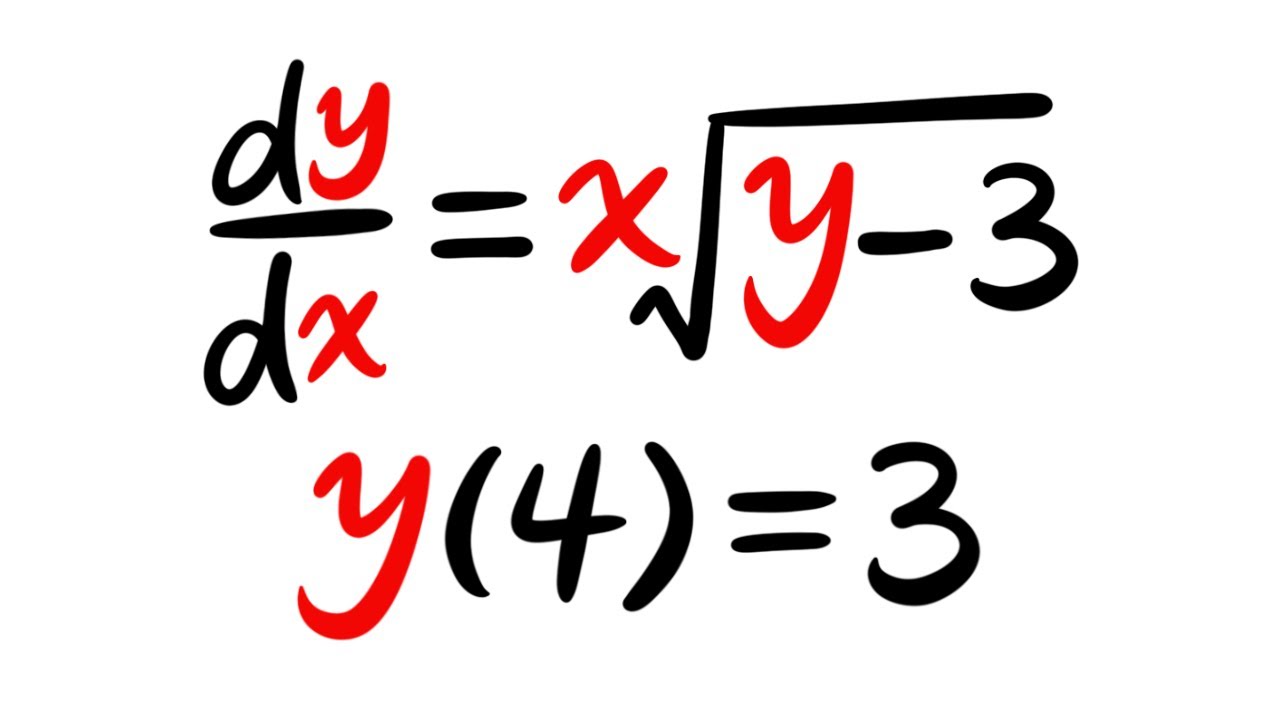
The Cauchy-Lipschitz theorem, also known as the existence and uniqueness theorem, is a fundamental concept in the field of mathematical analysis. This theorem plays a crucial role in understanding the solutions of ordinary differential equations, providing essential insights into the behavior of dynamical systems and physical phenomena. By establishing the conditions under which a unique solution to an initial value problem exists, the theorem offers valuable guidance in various scientific and engineering disciplines.
Understanding the Cauchy-Lipschitz theorem involves delving into the intricate interplay between differential equations, initial conditions, and the properties of the functions involved. This theorem's significance extends beyond theoretical mathematics, finding practical applications in diverse fields such as physics, engineering, and economics. By unraveling the key facts about the Cauchy-Lipschitz theorem, we can gain a deeper appreciation for its impact on mathematical modeling and problem-solving. Let's explore eight essential facts that shed light on the profound implications of this fundamental theorem.
Key Takeaways:
- The Cauchy-Lipschitz Theorem guarantees a unique solution to certain math problems, helping us understand how things change over time in the real world.
- Named after two cool mathematicians, this theorem is like a secret code that unlocks the mysteries of nature, from physics to biology, and helps us make cool predictions!
The Cauchy-Lipschitz Theorem is a fundamental concept in mathematics.
The Cauchy-Lipschitz Theorem, also known as the Existence and Uniqueness Theorem, is a fundamental concept in the field of differential equations. It provides crucial insights into the existence and uniqueness of solutions to initial value problems for ordinary differential equations. This theorem plays a pivotal role in various scientific and engineering disciplines, making it a cornerstone of mathematical analysis.
It guarantees the existence of a unique solution under certain conditions.
The Cauchy-Lipschitz Theorem guarantees the existence of a unique solution to an initial value problem for a first-order ordinary differential equation under specific conditions. This assurance of a singular solution is invaluable in practical applications, as it provides a mathematical foundation for predicting and understanding the behavior of dynamic systems.
The theorem is named after Augustin-Louis Cauchy and Rudolf Lipschitz.
The theorem is named in honor of the mathematicians Augustin-Louis Cauchy and Rudolf Lipschitz, who made significant contributions to the development of mathematical analysis and differential equations. Their pioneering work laid the groundwork for this essential theorem, which continues to shape the study of dynamical systems and mathematical modeling.
It is a key tool in analyzing dynamical systems.
The Cauchy-Lipschitz Theorem serves as a key tool in the analysis of dynamical systems, allowing researchers and practitioners to gain deep insights into the behavior and evolution of various physical, biological, and economic systems. By providing a framework for understanding the uniqueness and existence of solutions, this theorem facilitates the study and comprehension of complex dynamic phenomena.
The theorem has wide-ranging applications in diverse fields.
The Cauchy-Lipschitz Theorem finds applications in diverse fields such as physics, engineering, biology, economics, and environmental science. Its utility in modeling and understanding real-world phenomena underscores its significance in advancing scientific knowledge and technological innovation.
It establishes a vital link between theory and real-world phenomena.
By establishing the existence and uniqueness of solutions to differential equations, the Cauchy-Lipschitz Theorem bridges the gap between theoretical mathematical concepts and their practical applications in the real world. This connection is essential for developing accurate models and making predictions in various scientific and engineering domains.
The theorem's conditions are essential for ensuring a unique solution.
The conditions specified in the Cauchy-Lipschitz Theorem are crucial for ensuring the existence and uniqueness of solutions to initial value problems. These conditions provide a rigorous framework for analyzing and determining the behavior of differential equations, laying the groundwork for robust and reliable mathematical modeling.
It forms the basis for advanced studies in differential equations and dynamical systems.
The Cauchy-Lipschitz Theorem serves as a foundational concept for advanced studies in differential equations, dynamical systems, and mathematical modeling. Its principles underpin higher-level mathematical theories and methodologies, shaping the way researchers approach complex dynamic phenomena and develop sophisticated mathematical models.
The Cauchy-Lipschitz Theorem, also known as the Existence and Uniqueness Theorem, is a fundamental concept in the field of differential equations. It provides crucial insights into the existence and uniqueness of solutions to initial value problems for ordinary differential equations. This theorem plays a pivotal role in various scientific and engineering disciplines, making it a cornerstone of mathematical analysis.
The Cauchy-Lipschitz Theorem guarantees the existence of a unique solution to an initial value problem for a first-order ordinary differential equation under specific conditions. This assurance of a singular solution is invaluable in practical applications, as it provides a mathematical foundation for predicting and understanding the behavior of dynamic systems.
The theorem is named in honor of the mathematicians Augustin-Louis Cauchy and Rudolf Lipschitz, who made significant contributions to the development of mathematical analysis and differential equations. Their pioneering work laid the groundwork for this essential theorem, which continues to shape the study of dynamical systems and mathematical modeling.
The Cauchy-Lipschitz Theorem serves as a key tool in the analysis of dynamical systems, allowing researchers and practitioners to gain deep insights into the behavior and evolution of various physical, biological, and economic systems. By providing a framework for understanding the uniqueness and existence of solutions, this theorem facilitates the study and comprehension of complex dynamic phenomena.
The Cauchy-Lipschitz Theorem finds applications in diverse fields such as physics, engineering, biology, economics, and environmental science. Its utility in modeling and understanding real-world phenomena underscores its significance in advancing scientific knowledge and technological innovation.
By establishing the existence and uniqueness of solutions to differential equations, the Cauchy-Lipschitz Theorem bridges the gap between theoretical mathematical concepts and their practical applications in the real world. This connection is essential for developing accurate models and making predictions in various scientific and engineering domains.
The conditions specified in the Cauchy-Lipschitz Theorem are crucial for ensuring the existence and uniqueness of solutions to initial value problems. These conditions provide a rigorous framework for analyzing and determining the behavior of differential equations, laying the groundwork for robust and reliable mathematical modeling.
The Cauchy-Lipschitz Theorem serves as a foundational concept for advanced studies in differential equations, dynamical systems, and mathematical modeling. Its principles underpin higher-level mathematical theories and methodologies, shaping the way researchers approach complex dynamic phenomena and develop sophisticated mathematical models.
Conclusion
In conclusion, the Cauchy-Lipschitz Theorem, also known as the Existence and Uniqueness Theorem, plays a pivotal role in the field of differential equations. Understanding the conditions and implications of this theorem is crucial for mathematicians, scientists, and engineers working with dynamical systems. By providing a framework for ensuring the existence and uniqueness of solutions to differential equations, this theorem serves as a fundamental tool in various applications, from modeling physical phenomena to optimizing engineering designs. Its significance cannot be overstated, as it underpins the reliability and predictability of mathematical models in diverse real-world scenarios.
FAQs
Q: What is the significance of the Cauchy-Lipschitz Theorem in real-world applications?
A: The Cauchy-Lipschitz Theorem, or Existence and Uniqueness Theorem, is of paramount importance in real-world applications involving dynamical systems, such as in physics, engineering, and economics. It ensures that solutions to differential equations exist and are unique under certain conditions, providing a solid foundation for modeling and predicting various phenomena.
Q: How does the Cauchy-Lipschitz Theorem impact the study of differential equations?
A: The Cauchy-Lipschitz Theorem significantly influences the study of differential equations by establishing criteria for the existence and uniqueness of solutions. This theorem enables mathematicians and scientists to rigorously analyze and solve differential equations, forming the basis for understanding dynamic systems and their behavior.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
