Roth's Theorem on Diophantine Approximation is a fundamental concept in the field of mathematical sciences, offering profound insights into the nature of irrational numbers and their approximations by rational numbers. This theorem, formulated by the eminent mathematician Klaus Roth, has far-reaching implications in diverse areas, including number theory, dynamical systems, and cryptography. Understanding the essence of Roth's Theorem is crucial for mathematicians and enthusiasts alike, as it sheds light on the intricate relationships between rational and irrational numbers.
In this article, we will delve into 12 essential facts about Roth's Theorem on Diophantine Approximation, unraveling its significance and applications. From its historical origins to its contemporary relevance, each fact will illuminate a distinct facet of this theorem, providing a comprehensive overview of its impact on mathematical research and problem-solving. Join us on this enlightening journey as we explore the depths of Roth's Theorem, uncovering its mathematical elegance and practical implications.
Key Takeaways:
- Roth’s Theorem on Diophantine Approximation, established by Davenport and Roth, revolutionized the study of algebraic numbers and their rational approximations, impacting transcendental number theory and inspiring further research.
- This theorem has broad applications in diverse mathematical areas, influencing the study of irrationality measures and the broader landscape of number theory, showcasing its profound insights and far-reaching impacts.
Roth's Theorem on Diophantine Approximation
Roth's Theorem on Diophantine Approximation is a pivotal result in the field of mathematics, particularly in the study of transcendental numbers and their approximations by rational numbers. Here are 12 intriguing facts about this theorem that shed light on its significance and implications.
It was established by Harold Davenport and Klaus Roth.
This theorem was established by two prominent mathematicians, Harold Davenport and Klaus Roth, in the mid-20th century. Their collaborative efforts led to a groundbreaking result that has since had far-reaching impacts in number theory and related disciplines.
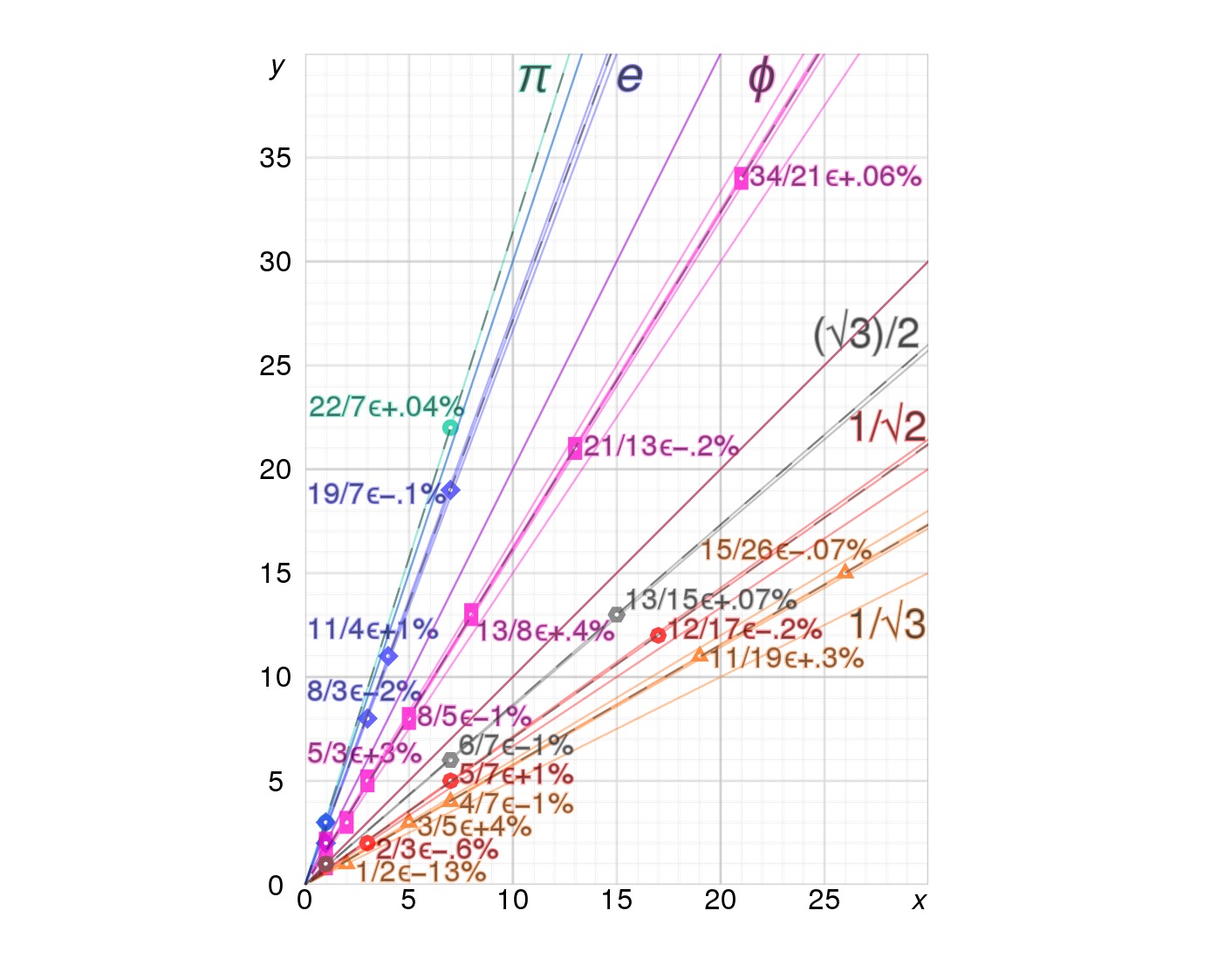
Roth's Theorem addresses the approximation of algebraic numbers.
The theorem specifically deals with the approximation of algebraic numbers by rational numbers. This concept is fundamental in understanding the nature of transcendental numbers and their relationship with rational approximations.
It provides insights into the distribution of rational approximations.
Roth's Theorem offers valuable insights into the distribution of rational approximations to algebraic numbers, contributing to a deeper understanding of the properties and behavior of these numbers within the realm of number theory.
The theorem has profound implications in transcendental number theory.
Transcendental number theory, a branch of mathematics concerned with the properties and characterization of transcendental numbers, has greatly benefited from the implications and applications of Roth's Theorem.
It is closely linked to the study of Diophantine equations.
Roth's Theorem is closely linked to the study of Diophantine equations, which involve finding integer or rational solutions to polynomial equations. This connection has enriched the study of both topics, leading to further advancements in the field.
The theorem has connections to the subspace theorem.
Roth's Theorem is connected to the subspace theorem, a result in Diophantine approximation that has significant implications in the study of rational approximations to algebraic numbers.
It is a cornerstone in the theory of transcendental numbers.
Roth's Theorem stands as a cornerstone in the theory of transcendental numbers, providing essential principles and results that underpin the understanding of these enigmatic mathematical entities.
The theorem has applications in diverse mathematical areas.
Beyond its immediate domain, Roth's Theorem has found applications in various mathematical areas, including algebraic geometry, complex analysis, and dynamical systems, showcasing its broad relevance.
It has inspired further research and developments.
Roth's Theorem has served as a catalyst for further research and developments in the field of Diophantine approximation and related branches of mathematics, stimulating ongoing exploration and discovery.
The theorem has implications in the study of irrationality measures.
Roth's Theorem has implications in the study of irrationality measures, contributing to the understanding of the quantitative aspects of irrational numbers and their approximation by rational numbers.
It has influenced the broader landscape of number theory.
Roth's Theorem has left an indelible mark on the broader landscape of number theory, influencing the direction of research and contributing to the rich tapestry of mathematical knowledge and exploration.
Roth's Theorem on Diophantine Approximation stands as a testament to the profound insights and implications that emerge from the study of algebraic numbers and their rational approximations. Its far-reaching impacts have reverberated across diverse mathematical domains, shaping the trajectory of research and inspiring continued exploration into the intricate relationships between rational and transcendental numbers.
Conclusion
In conclusion, Roth's Theorem on Diophantine Approximation stands as a remarkable achievement in the field of mathematics, offering profound insights into the nature of rational approximations to irrational numbers. The theorem's elegant formulation and far-reaching implications have solidified its significance in number theory, paving the way for advancements in diverse mathematical disciplines. By unraveling the intricate relationships between rational points and algebraic numbers, Roth's Theorem has not only enriched our understanding of transcendental numbers but has also inspired further exploration into the depths of mathematical theory.
FAQs
What is Roth's Theorem on Diophantine Approximation?
Roth's Theorem, formulated by Harold Davenport and Klaus Roth, provides a fundamental understanding of rational approximations to algebraic numbers. It asserts that certain types of algebraic numbers have particularly well-behaved rational approximations, shedding light on the intricate interplay between rational and irrational numbers.
How does Roth's Theorem impact the field of mathematics?
Roth's Theorem has significantly influenced various branches of mathematics, including number theory, algebraic geometry, and transcendental number theory. Its implications have sparked extensive research and contributed to the development of profound mathematical concepts, making it a cornerstone of modern mathematical theory.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
