Green's theorem is a fundamental concept in the field of mathematical sciences, particularly in the study of vector calculus and its applications. This theorem, named after the British mathematician George Green, establishes a powerful relationship between line integrals and double integrals over a region in the plane. Understanding Green's theorem is crucial for solving a wide range of problems in physics, engineering, and other scientific disciplines. In this article, we will delve into eight essential facts about Green's theorem, shedding light on its significance, applications, and underlying principles. By exploring these key insights, readers will gain a deeper appreciation for the elegance and utility of Green's theorem, as well as its role in shaping our understanding of mathematical and physical phenomena. Let's embark on a journey to unravel the intricacies of Green's theorem and uncover its profound impact on the world of mathematics and beyond.
Key Takeaways:
- Green’s Theorem is a powerful tool that connects double integrals and line integrals, making it essential for solving real-world problems in physics and engineering.
- Named after mathematician George Green, this theorem provides a link between line integrals and double integrals, playing a crucial role in diverse scientific disciplines.
Green's Theorem is a fundamental concept in the field of mathematics.
Green's Theorem is a fundamental principle in the realm of mathematics that establishes a relationship between a double integral over a region and a line integral around the boundary of that region. It is a pivotal theorem in the study of vector calculus and plays a crucial role in various mathematical applications, particularly in the field of physics and engineering.
It is named after the British mathematician George Green.
The theorem is named after the renowned British mathematician George Green, who formulated the theorem in the 1830s. George Green's significant contributions to the field of mathematics have left an indelible mark, and his theorem continues to be a cornerstone of mathematical analysis.
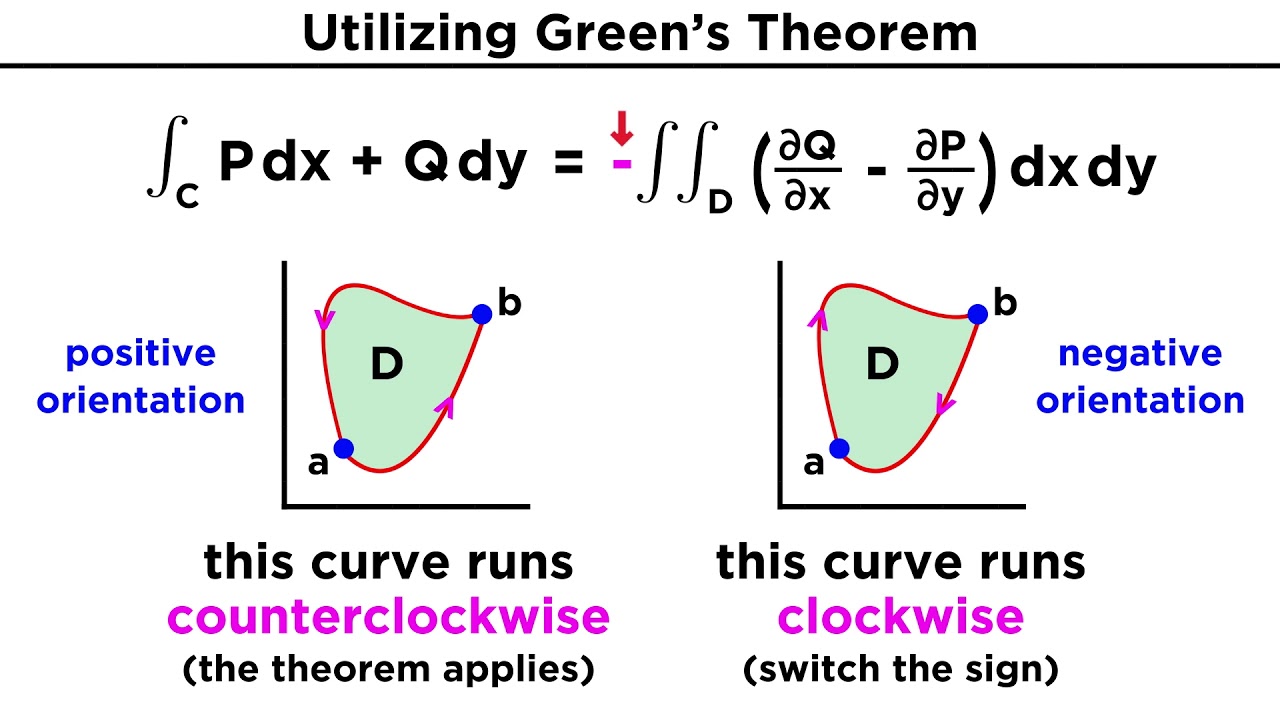
Green's Theorem relates a double integral over a region to a line integral around the boundary of the region.
This theorem establishes a profound connection between the line integral of a vector field over a simple closed curve and the double integral of the divergence of the vector field over the region enclosed by the curve. This relationship provides a powerful tool for evaluating integrals and solving various problems in diverse scientific disciplines.
It is a fundamental theorem in the field of vector calculus.
Green's Theorem holds immense significance in the realm of vector calculus, serving as a fundamental principle that facilitates the computation of line integrals and double integrals over various regions. Its applications extend to diverse areas such as fluid dynamics, electromagnetism, and more.
Green's Theorem is a special case of Stokes' Theorem in higher dimensions.
In the context of higher dimensions, Green's Theorem is considered a special case of Stokes' Theorem, which generalizes the concept to higher-dimensional manifolds. This connection underscores the broader implications and applications of Green's Theorem in advanced mathematical contexts.
It provides a link between the line integral and the double integral.
One of the key insights offered by Green's Theorem is the establishment of a direct link between the line integral of a vector field and the double integral of the divergence of the same vector field. This linkage enables mathematicians and scientists to seamlessly transition between these two integral forms, simplifying complex calculations and analyses.
Green's Theorem is essential for solving problems in physics and engineering.
The theorem's utility extends beyond the realm of pure mathematics, finding crucial applications in the fields of physics and engineering. It provides a powerful method for solving problems related to fluid flow, electromagnetic fields, and other physical phenomena, making it an indispensable tool for researchers and practitioners in these domains.
It is a key component of the Gauss–Green formula.
Green's Theorem serves as a foundational element of the Gauss–Green formula, which establishes a connection between surface integrals and volume integrals. This formula plays a pivotal role in various mathematical and physical contexts, further underscoring the significance of Green's Theorem in advanced mathematical theories and applications.
Conclusion
In conclusion, Green's Theorem is a powerful tool in the field of mathematical sciences, providing a fundamental connection between line integrals and double integrals over a region. Understanding the key concepts and applications of Green's Theorem is essential for tackling various problems in physics, engineering, and other scientific disciplines. By grasping the significance of circulation and flux, as well as the conditions for its applicability, individuals can harness the theorem's potential to simplify complex calculations and gain deeper insights into vector fields and their behavior. Embracing the principles behind Green's Theorem opens up a world of possibilities for analyzing and solving diverse real-world scenarios, making it a cornerstone of advanced mathematical reasoning and problem-solving.
FAQs
What is the significance of Green's Theorem?Green's Theorem establishes a crucial relationship between line integrals and double integrals over a region in the plane. It provides a powerful method for evaluating circulation and flux of a vector field, offering a streamlined approach to solving various problems in physics, engineering, and mathematics.
How is Green's Theorem applied in real-world scenarios?Green's Theorem finds applications in diverse real-world scenarios, such as calculating work done by a force, determining fluid flow, and analyzing electromagnetic fields. Its ability to simplify complex calculations and provide insights into vector fields makes it an invaluable tool in scientific and engineering disciplines.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
