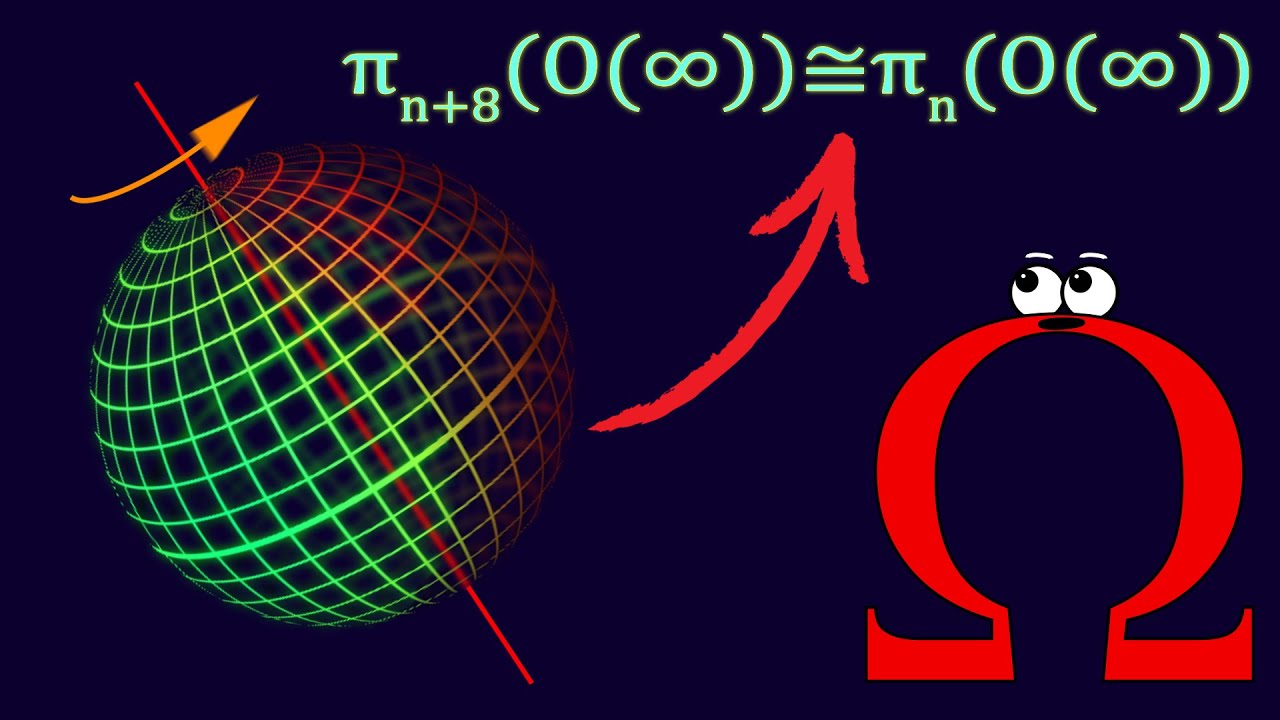
The Bott Periodicity Theorem is a fascinating concept in mathematics that has intrigued scholars and enthusiasts for decades. It delves into the intricate patterns and periodicity found in algebraic topology, offering profound insights into the structure of certain mathematical objects. Understanding the essence of this theorem requires delving into the realms of homotopy theory, K-theory, and complex geometry, making it a captivating subject for mathematicians and researchers.
In this article, we will unravel the enigmatic nature of the Bott Periodicity Theorem, shedding light on its significance and applications. From its historical origins to its modern-day implications in various mathematical disciplines, we will explore nine compelling facts that will deepen your understanding of this profound theorem. Whether you're a seasoned mathematician, a curious student, or an avid learner with a passion for mathematical sciences, this exploration of the Bott Periodicity Theorem promises to be an enlightening journey into the depths of mathematical theory and its real-world implications.
Key Takeaways:
- Bott Periodicity Theorem is a captivating concept in mathematics, revealing mesmerizing patterns in K-theory and shedding light on cyclical behavior in homotopy groups.
- Pioneered by Raoul Bott, this theorem has far-reaching applications in theoretical physics, inspiring ongoing research and representing a triumph of mathematical ingenuity.
Bott Periodicity Theorem: A Fascinating Mathematical Phenomenon
Bott Periodicity Theorem is a captivating concept in mathematics that has intrigued scholars and mathematicians for decades. Let's delve into 9 intriguing facts about this remarkable theorem.
Bott Periodicity Theorem is a Fundamental Concept in Algebraic Topology
This theorem plays a pivotal role in algebraic topology, a branch of mathematics that explores the properties of spaces and structures. It provides profound insights into the periodicity of certain mathematical structures.
It Unveils a Striking Pattern in K-Theory
Bott Periodicity Theorem reveals a mesmerizing pattern in K-theory, a branch of mathematics that classifies certain mathematical objects called "vector bundles." This pattern showcases a remarkable periodicity, offering a deeper understanding of these structures.
The Theorem Was Pioneered by Raoul Bott
Raoul Bott, a distinguished mathematician, formulated the Bott Periodicity Theorem, leaving an indelible mark on the field of mathematics. His groundbreaking work continues to inspire and influence mathematicians worldwide.
It Demonstrates Cyclical Behavior in Homotopy Groups
Bott Periodicity Theorem sheds light on the cyclical nature of homotopy groups, which are essential invariants in algebraic topology. This theorem unveils the intricate periodic behavior inherent in these groups, unraveling a captivating mathematical phenomenon.
The Theorem Has Far-Reaching Applications in Theoretical Physics
In the realm of theoretical physics, Bott Periodicity Theorem finds profound applications, particularly in the study of phenomena such as string theory and quantum mechanics. Its implications extend into diverse areas of theoretical physics, enriching our comprehension of fundamental concepts.
It Offers Insights into Stable Homotopy Theory
Stable homotopy theory, a cornerstone of algebraic topology, benefits significantly from the profound insights provided by Bott Periodicity Theorem. This theorem illuminates the stable homotopy groups of spheres, unraveling deep-seated connections within this mathematical framework.
Bott Periodicity Theorem Inspires Ongoing Research and Exploration
The theorem continues to inspire mathematicians and researchers to delve into its intricacies, fostering ongoing exploration and discovery. Its enigmatic properties fuel a vibrant field of study, driving the quest for deeper comprehension and new insights.
It Represents a Triumph of Mathematical Ingenuity
Bott Periodicity Theorem stands as a testament to the triumph of mathematical ingenuity, showcasing the profound elegance and depth of mathematical concepts. Its enduring significance underscores the timeless allure of mathematical exploration.
In conclusion, Bott Periodicity Theorem stands as a captivating and fundamental concept in mathematics, offering profound insights into algebraic topology, K-theory, and theoretical physics. Its enduring legacy continues to inspire mathematicians and researchers, driving the ongoing quest for deeper understanding and new discoveries.
Conclusion
In conclusion, the Bott Periodicity Theorem is a fascinating concept that has far-reaching implications in various branches of mathematics and theoretical physics. Its discovery has significantly contributed to our understanding of periodicity in algebraic K-theory and homotopy theory, shedding light on the intricate connections between these seemingly disparate fields. By uncovering the underlying patterns and structures within these domains, the theorem has paved the way for groundbreaking advancements and continues to inspire new avenues of research. As mathematicians and physicists delve deeper into the implications of Bott periodicity, the theorem's profound significance in the fabric of mathematical sciences becomes increasingly apparent, shaping the landscape of theoretical exploration and discovery.
FAQs
What is the significance of Bott Periodicity Theorem?The Bott Periodicity Theorem holds immense significance in algebraic K-theory and homotopy theory, providing deep insights into the periodic behavior of certain mathematical structures. It has profound implications in understanding the fundamental nature of these fields and has paved the way for significant advancements in theoretical mathematics and physics.
How does Bott Periodicity Theorem impact current research in mathematics and theoretical physics?The Bott Periodicity Theorem continues to influence and inspire current research in mathematics and theoretical physics by revealing profound connections between seemingly disparate areas of study. Its implications have led to the exploration of new mathematical structures and the development of innovative theoretical frameworks, shaping the trajectory of ongoing research endeavors.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.


