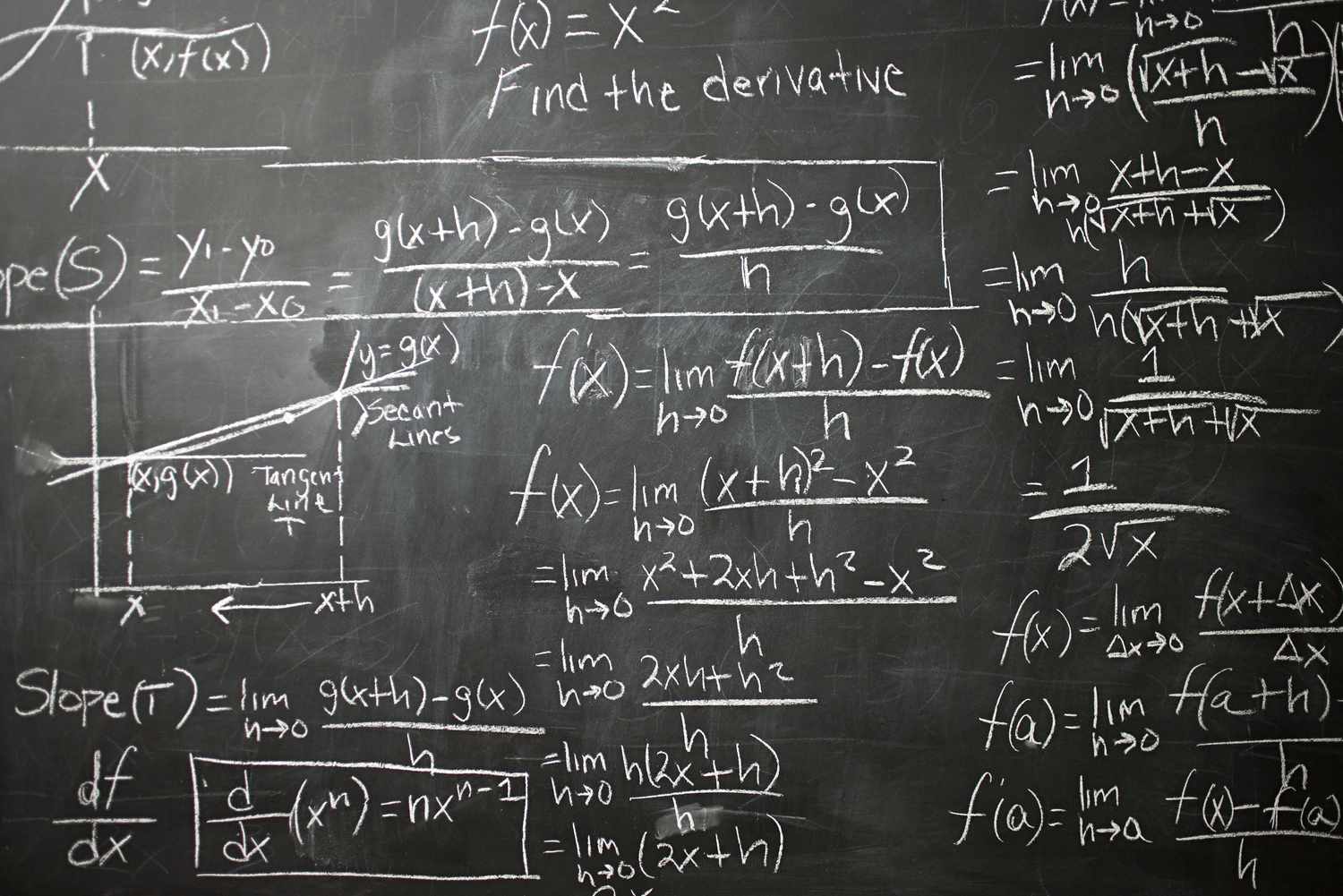
Calculus, a fundamental branch of mathematics, has significantly influenced various fields such as physics, engineering, economics, and computer science. Its concepts and principles have revolutionized our understanding of change and motion. In this article, we will explore 20 intriguing facts about calculus, shedding light on its historical significance, practical applications, and theoretical underpinnings.
Let's embark on a captivating journey through the world of calculus, unraveling its profound impact on the way we comprehend the natural world and solve complex problems. Whether you're a student delving into the intricacies of calculus for the first time or a curious mind seeking to deepen your knowledge, these facts will offer valuable insights into the beauty and utility of this mathematical discipline. So, buckle up and get ready to uncover the fascinating facets of calculus that have shaped the modern world.
Key Takeaways:
- Calculus, developed by Newton and Leibniz, helps us understand change and motion. It’s used in physics, engineering, and even medicine to solve real-world problems and make groundbreaking discoveries.
- By studying Calculus, we can analyze complex systems, model growth and decay, and develop critical thinking skills. It’s a dynamic field that empowers us to explore the world through a mathematical lens.
Calculus is a branch of mathematics developed independently by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century.
Often referred to as the "mathematics of change," Calculus provides a framework for understanding and analyzing processes that involve varying quantities. It encompasses the study of limits, derivatives, integrals, and infinite series, making it a fundamental tool in fields such as physics, engineering, economics, and computer science.
The two main branches of Calculus are differential calculus and integral calculus.
Differential calculus focuses on the concept of the derivative, which measures the rate of change of a function. Integral calculus, on the other hand, deals with the concept of the integral, which represents the accumulation of quantities. These two branches are interconnected through the fundamental theorem of calculus, which establishes the relationship between derivatives and integrals.
Calculus is instrumental in understanding motion and change.
By utilizing calculus, scientists and engineers can study the motion of objects, model population growth, analyze the behavior of systems, and predict future trends. This mathematical discipline provides a powerful set of tools for investigating dynamic phenomena and solving real-world problems.
The foundations of Calculus can be traced back to ancient times.
The method of exhaustion, developed by ancient Greek mathematicians, laid the groundwork for integral calculus. Additionally, the concept of infinitesimals, which are infinitely small quantities, played a crucial role in the development of Calculus.
Calculus has widespread applications in various fields.
From determining the optimal shape of structures to analyzing the flow of fluids, Calculus plays a pivotal role in diverse areas. It is used in designing roller coasters, understanding the behavior of electrical circuits, and even in the field of medicine for modeling biological processes.
The fundamental theorem of calculus connects the two branches of Calculus.
This theorem establishes the relationship between differentiation and integration, providing a powerful tool for evaluating integrals and understanding the behavior of functions. It is a cornerstone of Calculus and underpins many of its applications in science and engineering.
Calculus has contributed to groundbreaking scientific discoveries.
The use of Calculus was instrumental in Isaac Newton's formulation of the laws of motion and universal gravitation. Furthermore, it has been pivotal in the development of quantum mechanics, general relativity, and other areas of physics.
The concept of limits is fundamental to Calculus.
Limits are essential for understanding continuity, derivatives, and integrals. They form the basis for defining instantaneous rates of change and the area under curves, making them a fundamental concept in both differential and integral calculus.
The invention of Calculus revolutionized mathematics and science.
The introduction of Calculus provided a systematic framework for dealing with rates of change and accumulation, leading to significant advancements in the understanding of the natural world and the development of modern technology.
Calculus is crucial for understanding exponential growth and decay.
The study of exponential functions and their derivatives is essential for modeling phenomena such as population growth, radioactive decay, and the spread of diseases. Calculus provides the tools to analyze and predict the behavior of these dynamic processes.
The concept of derivatives lies at the heart of Calculus.
Derivatives represent the rate of change of a function and are used to analyze the behavior of functions, optimize processes, and solve problems in various fields. They are fundamental to understanding the instantaneous behavior of quantities.
Calculus enables the precise calculation of areas and volumes.
Integral calculus allows for the accurate determination of areas enclosed by curves and the volumes of complex shapes. This capability is invaluable in engineering, physics, and economics for calculating quantities such as work, fluid flow, and economic surplus.
The study of Calculus fosters critical thinking and problem-solving skills.
Engaging with the concepts and techniques of Calculus helps develop analytical reasoning, logical deduction, and creative problem-solving abilities. These skills are not only valuable in mathematics but also in a wide range of professional and academic pursuits.
Calculus has a rich history and has evolved over centuries.
From its origins in ancient mathematics to its modern applications in technology and science, Calculus has undergone continuous development and refinement. Its evolution reflects the ongoing quest to understand and quantify the natural world.
The use of Calculus extends to fields beyond traditional mathematics and science.
In fields such as economics, social sciences, and environmental studies, Calculus provides valuable tools for modeling and analyzing complex systems and phenomena. Its interdisciplinary applications highlight its broad relevance.
Calculus has practical applications in engineering and technology.
From designing efficient structures to developing algorithms for machine learning, Calculus plays a vital role in engineering and technology. It provides the mathematical foundation for solving problems related to optimization, dynamics, and signal processing.
The study of Calculus opens doors to advanced mathematical concepts.
By delving into Calculus, learners encounter advanced mathematical ideas such as infinite series, differential equations, and multivariable calculus. These concepts form the basis for further exploration in higher mathematics and related fields.
Calculus is a dynamic and evolving field of study.
Continual advancements in mathematics and its applications lead to ongoing developments in Calculus. New techniques, theories, and applications continue to enrich and expand the scope of this foundational mathematical discipline.
Calculus is essential for understanding the behavior of complex systems.
In fields such as chaos theory, fluid dynamics, and quantum mechanics, Calculus provides the tools to analyze and comprehend the intricate behavior of complex systems. Its application in these areas contributes to a deeper understanding of natural phenomena.
The study of Calculus empowers individuals to explore the world through a mathematical lens.
By equipping learners with the tools to analyze change, motion, and accumulation, Calculus enables a deeper understanding of the underlying principles governing the natural world. It fosters a perspective that embraces the dynamic and evolving nature of reality.
Calculus, often described as the mathematics of change, is a powerful and versatile branch of mathematics that has left an indelible mark on the world. Its foundational concepts, including limits, derivatives, and integrals, form the bedrock of modern science, engineering, and technology. From its ancient origins to its contemporary applications, Calculus has continually evolved and adapted, shaping our understanding of dynamic phenomena and enabling the precise analysis of complex systems. Through its interdisciplinary reach and profound influence, Calculus stands as a testament to the enduring impact of mathematical innovation and the quest to comprehend the ever-changing world around us.
Conclusion
In conclusion, calculus is a fascinating branch of mathematics that has revolutionized various fields, from physics and engineering to economics and biology. Its concepts, such as limits, derivatives, and integrals, have profoundly impacted our understanding of the world around us. Whether it's determining the velocity of a moving object, analyzing the growth of populations, or optimizing complex systems, calculus plays a pivotal role. As we continue to delve into the intricacies of this discipline, we uncover its profound influence on modern science and technology, shaping the way we perceive and interact with the universe.
FAQs
What are the practical applications of calculus?Calculus is widely used in various real-world applications, including engineering, physics, economics, and biology. It helps in modeling and analyzing systems such as motion, population growth, fluid dynamics, and electrical circuits.
Is calculus difficult to learn?While calculus can be challenging for some, it becomes more manageable with dedication and practice. Understanding the fundamental concepts and their applications is essential for mastering calculus. There are numerous resources, such as textbooks, online courses, and tutoring, available to support learning and comprehension.
Calculus enthusiasts, your mathematical journey continues! Explore the fundamental theorem of calculus, connecting derivatives and integrals seamlessly. Sard's theorem unveils the intricacies of critical points and level sets, while L'Hôpital's rule simplifies limits with indeterminate forms. Expand your calculus knowledge, sharpen problem-solving skills, and appreciate the elegance of these powerful mathematical tools. Click the links below to learn more fascinating facts about these essential calculus concepts.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
