The Poincaré-Bendixson Theorem is a fundamental concept in the field of dynamical systems and differential equations. It provides crucial insights into the behavior of solutions to certain types of dynamical systems, shedding light on the long-term trajectories of these systems. Understanding this theorem is essential for mathematicians, physicists, and engineers working with complex systems.
In this article, we will delve into 9 key facts about the Poincaré-Bendixson Theorem, unraveling its significance and applications. From its historical origins to its modern-day implications, we will explore the theorem's intricacies and real-world relevance. Whether you're a student delving into the realm of dynamical systems or a seasoned professional seeking to deepen your understanding, these facts will illuminate the power and utility of the Poincaré-Bendixson Theorem. So, let's embark on a journey through the fascinating world of dynamical systems and uncover the essential truths encapsulated within this theorem.
Key Takeaways:
- The Poincaré-Bendixson Theorem helps us understand how things move in a two-dimensional world and predicts when things will repeat their movements. It’s like a crystal ball for predicting the future of dynamical systems!
- This theorem is like a superhero for scientists and engineers, helping them understand and predict the behavior of everything from populations of animals to the flow of fluids. It’s like a secret code for unlocking the mysteries of the universe!
The Poincaré-Bendixson Theorem is a fundamental concept in dynamical systems.
The Poincaré-Bendixson Theorem, named after the French mathematician Henri Poincaré and the Scottish mathematician George David Birkhoff, is a crucial result in the field of dynamical systems. It provides essential insights into the behavior of solutions of differential equations, particularly in two-dimensional systems. The theorem addresses the existence of periodic orbits and the nature of the trajectories in the phase space, shedding light on the long-term dynamics of the system.
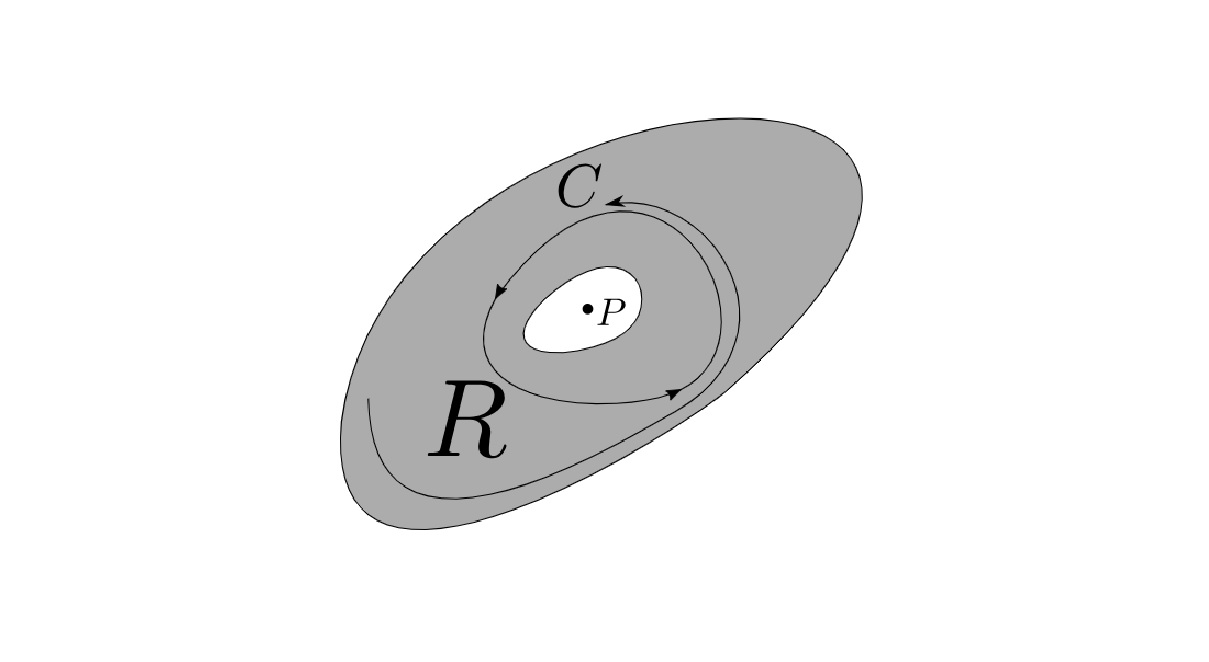
It establishes conditions for the existence of periodic orbits.
The theorem outlines the conditions under which a two-dimensional continuous dynamical system must have a closed orbit, or a periodic solution, within its phase space. This is a significant aspect of the theorem, as it offers a framework for understanding the presence of recurrent behavior in dynamic systems, which has broad applications in various scientific disciplines.
The theorem provides valuable insights into the behavior of solutions near fixed points.
One of the key implications of the Poincaré-Bendixson Theorem is its ability to characterize the behavior of solutions in the vicinity of fixed points. By examining the local dynamics near these critical points, the theorem offers a deeper understanding of the system's stability and the nature of its trajectories, contributing to the analysis of complex dynamical systems.
It plays a crucial role in the study of ecological and biological systems.
The Poincaré-Bendixson Theorem has significant applications in the study of ecological and biological systems, where dynamical models are employed to analyze population dynamics, predator-prey interactions, and other ecological phenomena. By providing insights into the long-term behavior of solutions, the theorem aids in predicting and understanding the dynamics of these complex systems.
The theorem has wide-ranging applications in physics and engineering.
Beyond its applications in mathematics, the Poincaré-Bendixson Theorem finds extensive use in physics and engineering. It offers valuable tools for analyzing the behavior of physical systems, such as oscillatory circuits, celestial mechanics, and fluid dynamics, enabling researchers and engineers to gain deeper insights into the underlying dynamics and stability of these systems.
It contributes to the understanding of chaos theory and nonlinear dynamics.
The theorem's implications extend to the realm of chaos theory and nonlinear dynamics, where it provides foundational principles for studying complex, unpredictable behavior in dynamical systems. By elucidating the existence of periodic orbits and the nature of trajectories, the theorem enriches the theoretical framework for analyzing chaotic systems, contributing to the broader understanding of nonlinear phenomena.
The theorem has historical significance in the development of dynamical systems theory.
The Poincaré-Bendixson Theorem holds historical significance in the evolution of dynamical systems theory, marking a pivotal advancement in the understanding of complex systems and their long-term behavior. Its contributions have reverberated across various scientific disciplines, shaping the trajectory of research in dynamical systems and nonlinear dynamics.
It has inspired further research and developments in dynamical systems.
The theorem's profound implications have inspired extensive research and advancements in the field of dynamical systems, spurring the development of sophisticated mathematical techniques and computational tools for analyzing complex dynamical behaviors. Its enduring impact continues to drive innovation and exploration in the study of nonlinear systems and their dynamics.
The theorem underscores the beauty and depth of mathematical theory.
Above all, the Poincaré-Bendixson Theorem underscores the beauty and depth of mathematical theory, showcasing the elegance and power of mathematical concepts in unraveling the mysteries of dynamical systems. Its enduring relevance and far-reaching applications exemplify the profound impact of mathematical principles in shaping our understanding of the natural world.
The Poincaré-Bendixson Theorem stands as a testament to the enduring legacy of mathematical insights, offering a profound understanding of the long-term behavior of dynamical systems and inspiring further exploration and innovation in the realm of nonlinear dynamics and complex systems.
Conclusion
In conclusion, the Poincaré-Bendixson Theorem is a powerful tool in the field of dynamical systems, providing crucial insights into the behavior of solutions to differential equations. Its applications extend across various disciplines, from physics and engineering to biology and economics. Understanding the theorem's implications and limitations is essential for researchers and practitioners seeking to analyze and predict the behavior of complex systems. By grasping the nine key facts about the Poincaré-Bendixson Theorem, one can gain a deeper appreciation for its significance and potential impact in diverse real-world scenarios.
FAQs
What is the significance of the Poincaré-Bendixson Theorem?The Poincaré-Bendixson Theorem is significant as it provides a fundamental tool for analyzing the long-term behavior of solutions to differential equations. It helps in identifying the existence of periodic orbits and understanding the stability of equilibrium points in dynamical systems.
How is the Poincaré-Bendixson Theorem applied in real-world scenarios?The theorem finds applications in various fields, including physics, biology, economics, and engineering. For instance, it can be used to study the behavior of ecological systems, analyze the stability of mechanical systems, and predict the dynamics of economic models.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
