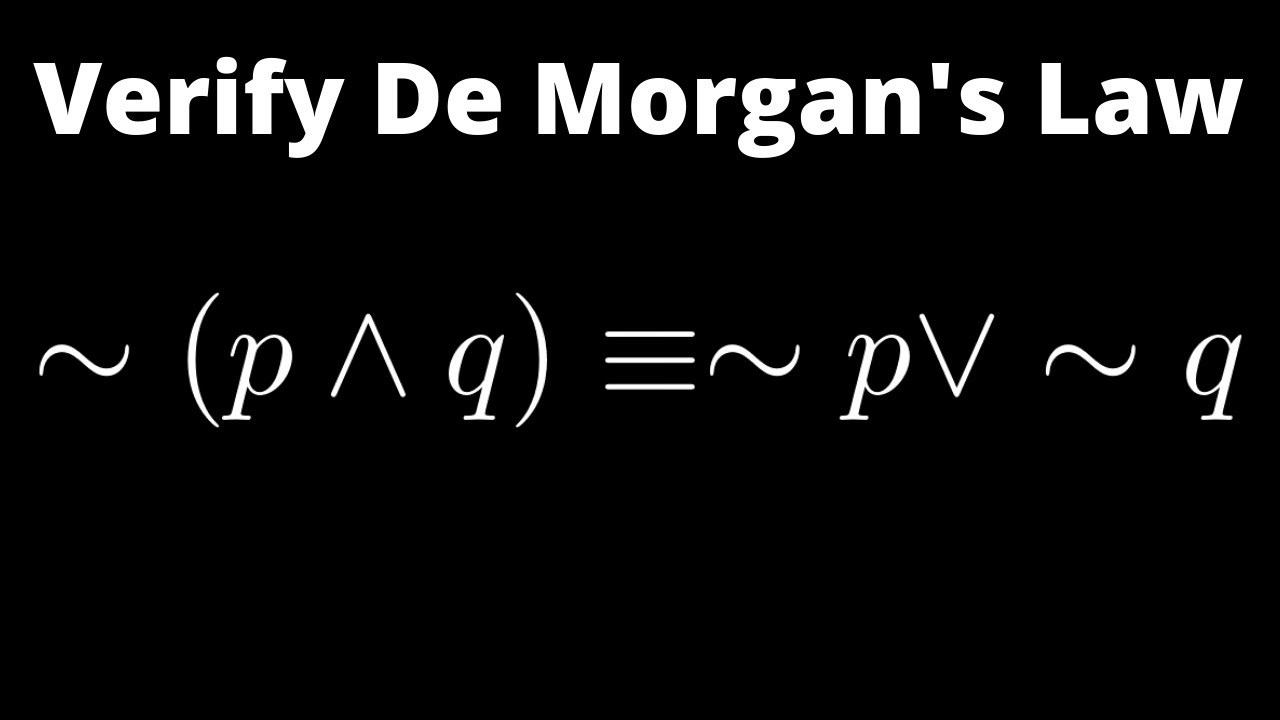
De Morgan's Laws are fundamental principles in the field of mathematical logic, playing a pivotal role in simplifying and transforming logical expressions. Named after the British mathematician Augustus De Morgan, these laws provide a set of rules for manipulating logical statements involving the concepts of "and" and "or." Understanding and applying De Morgan's Laws is crucial in various areas, including computer science, electrical engineering, and formal logic.
In this article, we will delve into seven essential facts about De Morgan's Laws, shedding light on their significance and practical applications. From their historical origins to their impact on digital circuit design and Boolean algebra, we will explore the multifaceted nature of these laws. By uncovering the intricacies of De Morgan's Laws, we aim to demystify their relevance and empower readers to leverage their transformative power in diverse problem-solving scenarios. Join us on this enlightening journey through the realm of logical reasoning and discover the profound impact of De Morgan's Laws.
Key Takeaways:
- De Morgan’s Laws are important rules in math that help simplify and solve problems with AND, OR, and NOT statements. They’re used in computer science, engineering, and digital circuit design to make things work better!
- Understanding De Morgan’s Laws can help people make digital devices work faster and better, solve complex problems in math and computer science, and improve how we process digital signals for things like audio and images.
De Morgan's Laws are fundamental principles in Boolean algebra.
De Morgan's Laws are essential principles in Boolean algebra, a branch of mathematical logic that deals with binary variables and operations. These laws are named after the British mathematician and logician Augustus De Morgan, who formulated them in the 19th century. They describe the relationships between logical conjunction (AND) and disjunction (OR) of statements involving negations. Understanding these laws is crucial in simplifying and manipulating logical expressions in various fields, including computer science, electrical engineering, and formal logic.
The laws describe the behavior of logical operations involving negations.
De Morgan's Laws provide a set of rules that explain how negations interact with logical conjunction and disjunction. The first law states that the negation of a conjunction is logically equivalent to the disjunction of the negations of the individual statements. Similarly, the second law states that the negation of a disjunction is logically equivalent to the conjunction of the negations of the individual statements. These laws play a pivotal role in transforming complex logical expressions into simpler forms, facilitating easier analysis and computation.
De Morgan's Laws find extensive applications in digital circuit design.
In the realm of digital circuit design, De Morgan's Laws are indispensable for simplifying and optimizing logic circuits. By applying these laws, engineers can streamline complex circuitry, reduce the number of components, and enhance overall efficiency. This application of the laws is crucial in the development of modern electronic devices, ranging from microprocessors and memory units to intricate integrated circuits used in various electronic systems.
They are utilized in theorem proving and formal verification.
De Morgan's Laws are instrumental in theorem proving and formal verification processes within the domain of mathematics and computer science. These laws enable mathematicians and computer scientists to manipulate logical expressions systematically, leading to the establishment of the validity of theorems and the verification of complex systems and algorithms. Their role in these areas highlights their significance in ensuring the accuracy and reliability of mathematical proofs and computational systems.
The laws enable the simplification of Boolean expressions.
One of the primary benefits of De Morgan's Laws is their ability to simplify Boolean expressions, making them more manageable for analysis and implementation. By leveraging these laws, engineers and mathematicians can reduce the complexity of logical statements and equations, leading to more efficient problem-solving and enhanced comprehension of intricate logical structures.
They are essential for understanding and implementing digital signal processing algorithms.
In the realm of digital signal processing, De Morgan's Laws play a crucial role in the development and implementation of algorithms for signal analysis and manipulation. By applying these laws, engineers and researchers can streamline the processing of digital signals, leading to advancements in areas such as telecommunications, audio processing, and image processing.
De Morgan's Laws are a cornerstone of logical reasoning and problem-solving.
In the broader context of logical reasoning and problem-solving, De Morgan's Laws serve as foundational principles that underpin the systematic analysis and manipulation of logical statements. Their pervasive influence extends across various disciplines, including mathematics, computer science, and engineering, where they empower professionals to tackle complex challenges with clarity and precision.
By understanding and applying De Morgan's Laws, individuals can enhance their ability to dissect and comprehend intricate logical structures, paving the way for advancements in diverse fields and the continued evolution of technological innovation.
Conclusion
In conclusion, De Morgan's Laws are fundamental principles in the field of mathematical logic, playing a crucial role in simplifying and transforming logical expressions. Understanding these laws empowers mathematicians, computer scientists, and engineers to manipulate complex logical statements with ease and precision. By recognizing the equivalence between logical operations, De Morgan's Laws enable the simplification of complex expressions, leading to more efficient problem-solving and decision-making processes. Embracing these laws opens up a world of possibilities for logical reasoning and problem-solving, making them an indispensable tool in various domains.
FAQs
What are De Morgan's Laws?De Morgan's Laws are a pair of fundamental principles in mathematical logic that describe the relationships between logical operations, specifically negation, conjunction, and disjunction. These laws provide a systematic way to simplify and transform logical expressions, enabling more efficient problem-solving and decision-making processes.
How are De Morgan's Laws applied in real-world scenarios?De Morgan's Laws have practical applications in various fields, including computer science, engineering, and mathematics. They are used to simplify logical expressions, optimize circuit designs, and enhance the efficiency of algorithms. Understanding and applying these laws can lead to more streamlined and effective problem-solving approaches in real-world scenarios.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
