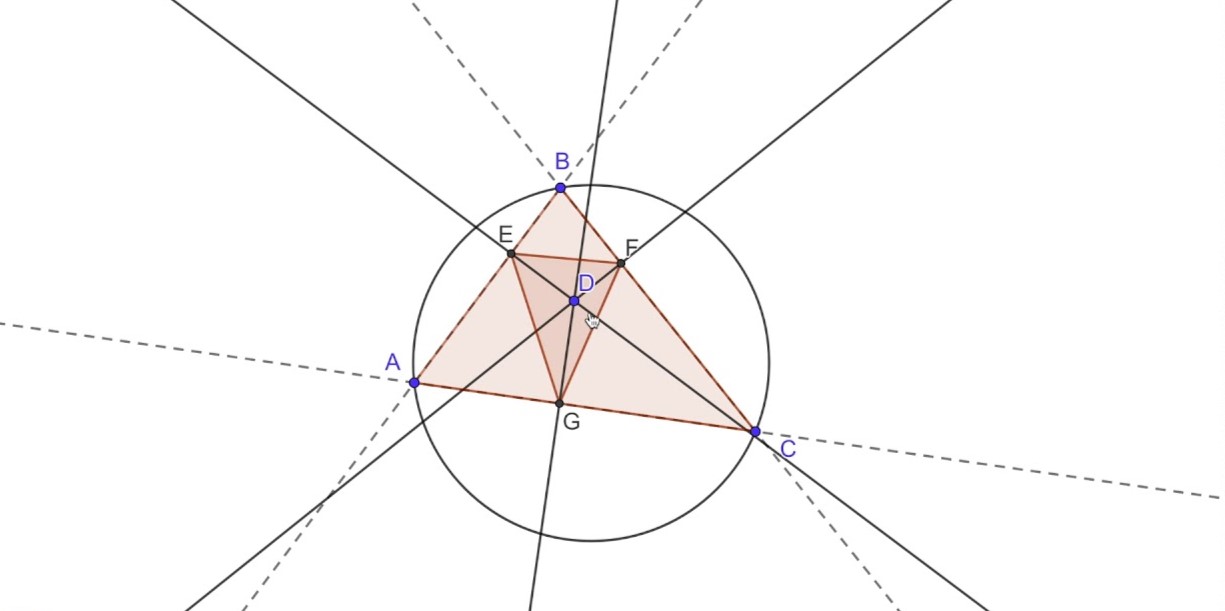
The Simson Line Theorem is a captivating concept in geometry that unveils intriguing relationships within a triangle. This theorem, named after the eminent mathematician Robert Simson, delves into the fascinating interplay between the circumcircle of a triangle and the points on its sides. By exploring the properties of the Simson Line, we gain valuable insights into the geometric configurations that arise from the interconnection of various elements within a triangle.
In this article, we will embark on an illuminating journey through 12 essential facts about the Simson Line Theorem. From its historical origins to its practical applications, we will unravel the significance of this theorem and its profound impact on the field of geometry. Join us as we delve into the depths of this captivating theorem, uncovering its intricacies and shedding light on its relevance in both theoretical and practical contexts. Let's embark on this geometric odyssey and unravel the mysteries of the Simson Line Theorem.
Key Takeaways:
- The Simson Line Theorem, named after Robert Simson, helps us understand the relationships between the vertices, circumcenter, and perpendiculars in a triangle, revealing fascinating geometric patterns.
- This theorem not only enriches our knowledge of geometry and trigonometry but also has practical applications in fields like architecture, engineering, and computer graphics, making it a valuable and captivating mathematical concept.
Simson Line Theorem is named after Robert Simson.
Robert Simson, a Scottish mathematician, is credited with discovering the Simson Line Theorem. This theorem, which bears his name, has significant applications in geometry and trigonometry.
The theorem is related to the circumcircle of a triangle.
The Simson Line Theorem is closely linked to the circumcircle of a triangle. It provides insights into the relationships between the vertices, circumcenter, and the feet of the perpendiculars from the vertices to the sides of the triangle.
It involves the concept of the Simson Line.
The theorem revolves around the Simson Line, a straight line associated with a given triangle and a point on its circumcircle. This line plays a crucial role in understanding the geometric properties described by the theorem.
The Simson Line Theorem connects various points in a triangle.
Through the Simson Line, the theorem establishes connections between the vertices of a triangle and the feet of the perpendiculars drawn from these vertices to the sides of the triangle. This interplay reveals intriguing patterns within the triangle.
It provides insights into cyclic quadrilaterals.
The Simson Line Theorem offers valuable insights into the properties of cyclic quadrilaterals inscribed in the circumcircle of a triangle. These relationships contribute to a deeper understanding of geometric configurations.
The theorem has applications in trigonometry.
Beyond its geometric implications, the Simson Line Theorem finds applications in trigonometry, particularly in the context of relationships between angles and sides within a triangle. This connection underscores the theorem's relevance in diverse mathematical domains.
It is a fundamental result in Euclidean geometry.
The Simson Line Theorem stands as a fundamental result in Euclidean geometry, enriching the understanding of the intricate interplay between the elements of a triangle and its circumcircle.
It unveils geometric patterns within a triangle.
By elucidating the relationships between the vertices, circumcenter, and the feet of the perpendiculars, the theorem unveils captivating geometric patterns within a triangle, enriching the study of geometric structures.
The theorem has practical applications in various fields.
The insights derived from the Simson Line Theorem have practical applications in fields such as architecture, engineering, and computer graphics, where an understanding of geometric principles is essential.
It is a subject of fascination for mathematicians and scholars.
The Simson Line Theorem continues to captivate mathematicians and scholars, inspiring further exploration and analysis to uncover its intricate properties and potential extensions.
The theorem contributes to the rich tapestry of mathematical knowledge.
As a significant result in geometry and trigonometry, the Simson Line Theorem contributes to the rich tapestry of mathematical knowledge, offering valuable perspectives on the intricate relationships within geometric configurations.
It underscores the elegance and depth of mathematical concepts.
The Simson Line Theorem exemplifies the elegance and depth of mathematical concepts, showcasing the beauty and complexity inherent in the study of geometry and trigonometry.
The Simson Line Theorem, named after Robert Simson, is a fundamental result in geometry and trigonometry. It is closely related to the circumcircle of a triangle and involves the concept of the Simson Line, which connects various points in a triangle. This theorem provides insights into cyclic quadrilaterals and has practical applications in fields such as architecture, engineering, and computer graphics. The Simson Line Theorem continues to fascinate mathematicians and scholars, contributing to the rich tapestry of mathematical knowledge and underscoring the elegance and depth of mathematical concepts.
Conclusion
In conclusion, the Simson Line Theorem is a fascinating concept in geometry that offers valuable insights into the relationships between points, lines, and circles within a triangle. Understanding the properties and applications of the Simson Line Theorem can greatly enhance one's grasp of geometric principles and their real-world implications. By delving into the twelve essential facts about this theorem, we have uncovered the intricate nature of this geometric phenomenon and its significance in various mathematical contexts. Whether exploring the theorem's historical origins or its practical applications in modern mathematics, the Simson Line Theorem continues to captivate mathematicians and learners alike with its timeless relevance and profound implications.
FAQs
What is the significance of the Simson Line Theorem?The Simson Line Theorem holds significant importance in geometry as it provides a deeper understanding of the relationships between points, lines, and circles within a triangle. By exploring this theorem, mathematicians gain valuable insights into the fundamental principles of geometry and their practical applications.
How can the Simson Line Theorem be applied in real-world scenarios?While the Simson Line Theorem is a fundamental concept in geometry, its applications extend beyond theoretical mathematics. In real-world scenarios, this theorem finds utility in fields such as engineering, architecture, and computer graphics, where geometric principles play a crucial role in design and problem-solving.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
