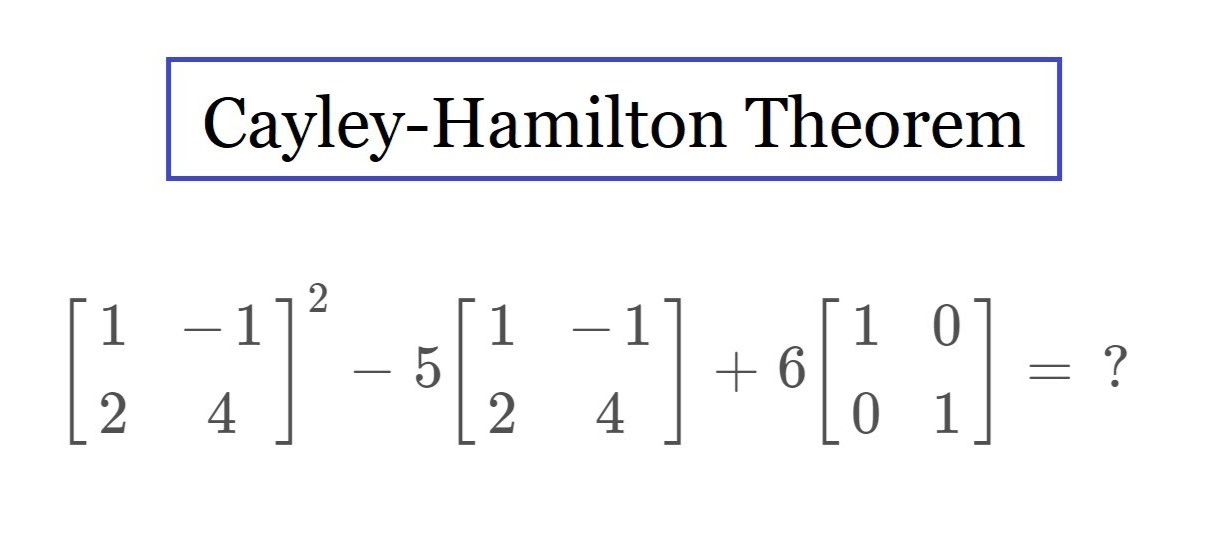
The Cayley-Hamilton theorem is a fundamental concept in linear algebra and matrix theory. It establishes a profound relationship between a square matrix and its own characteristic polynomial. This theorem, named after the mathematicians Arthur Cayley and William Hamilton, has wide-ranging applications in various fields, including physics, engineering, and computer science.
Understanding the Cayley-Hamilton theorem is crucial for comprehending the behavior of linear systems and solving practical problems in diverse domains. In this article, we will delve into 12 essential facts about the Cayley-Hamilton theorem, shedding light on its significance, applications, and implications in the realm of mathematical sciences. Whether you're a student delving into linear algebra or a professional seeking to deepen your understanding of matrix theory, these facts will provide valuable insights into this intriguing theorem and its relevance in the world of mathematics and beyond.
Key Takeaways:
- The Cayley-Hamilton Theorem is a powerful tool in math and engineering, helping simplify matrix calculations and solve problems in fields like physics and computer science.
- Named after mathematicians Cayley and Hamilton, the theorem has wide-ranging applications and has inspired profound developments in mathematical research and technology.
The Cayley-Hamilton Theorem is a fundamental concept in linear algebra.
The Cayley-Hamilton Theorem is a fundamental concept in linear algebra that has far-reaching implications in various fields of mathematics and engineering. It states that every square matrix satisfies its own characteristic equation. This theorem is named after the mathematicians Arthur Cayley and William Rowan Hamilton, who made significant contributions to the development of algebra and matrix theory. The theorem provides a powerful tool for simplifying calculations and solving problems related to matrices and linear transformations.
It is named after mathematicians Arthur Cayley and William Rowan Hamilton.
The Cayley-Hamilton Theorem is named after the prominent mathematicians Arthur Cayley and William Rowan Hamilton, who made substantial contributions to the fields of algebra and matrix theory. Arthur Cayley, a British mathematician, is renowned for his work in matrix theory and abstract algebra, while William Rowan Hamilton, an Irish mathematician, is celebrated for his contributions to optics, dynamics, and algebra. The theorem bearing their names stands as a testament to their profound impact on mathematical sciences.
The theorem provides a powerful tool for simplifying calculations and solving problems related to matrices and linear transformations.
The Cayley-Hamilton Theorem serves as a powerful tool for simplifying calculations and solving a wide array of problems related to matrices and linear transformations. By establishing a direct relationship between a matrix and its characteristic equation, this theorem enables mathematicians and engineers to streamline complex computations and gain deeper insights into the behavior of linear systems. Its applications extend to diverse fields, including control theory, signal processing, quantum mechanics, and computer graphics.
It is a cornerstone of matrix theory and linear algebra.
The Cayley-Hamilton Theorem stands as a cornerstone of matrix theory and linear algebra, providing a fundamental framework for understanding the properties and behavior of matrices. Its significance reverberates across various mathematical disciplines, laying the groundwork for advanced concepts and applications in areas such as eigenvalues, eigenvectors, diagonalization, and matrix exponentiation. This theorem forms an essential part of the mathematical toolkit used to analyze and manipulate matrices in both theoretical and practical contexts.
The theorem establishes a direct relationship between a matrix and its characteristic equation.
The Cayley-Hamilton Theorem establishes a direct relationship between a square matrix and its characteristic equation, which encapsulates essential information about the matrix's eigenvalues. This profound connection allows mathematicians and scientists to derive valuable insights into the behavior and properties of matrices, paving the way for innovative approaches to problem-solving and theoretical exploration in linear algebra and related fields.
It has wide-ranging applications in engineering, physics, and computer science.
The Cayley-Hamilton Theorem boasts wide-ranging applications across diverse domains, including engineering, physics, and computer science. Its utility extends to areas such as control systems, quantum mechanics, structural analysis, digital signal processing, and algorithm design. By leveraging the insights provided by this theorem, researchers and practitioners can tackle complex problems and devise efficient solutions in a multitude of technological and scientific endeavors.
The theorem plays a pivotal role in the study of linear transformations and dynamical systems.
The Cayley-Hamilton Theorem plays a pivotal role in the study of linear transformations and dynamical systems, offering valuable tools for analyzing the behavior and stability of these systems. Its influence permeates fields such as control theory, differential equations, and dynamical systems theory, where it empowers researchers to unravel intricate dynamics and develop robust methodologies for system modeling and analysis.
It provides a unifying perspective on the behavior of matrices and their associated characteristic polynomials.
The Cayley-Hamilton Theorem provides a unifying perspective on the behavior of matrices and their associated characteristic polynomials, shedding light on the intricate interplay between algebraic and geometric properties of linear transformations. This holistic view enables mathematicians and scientists to explore the deep connections between matrix theory and other branches of mathematics, fostering interdisciplinary insights and paving the way for innovative advancements in mathematical research.
The theorem has implications for the study of eigenvalues and eigenvectors.
The Cayley-Hamilton Theorem has profound implications for the study of eigenvalues and eigenvectors, offering a powerful framework for understanding the spectral properties of matrices and their relevance in diverse mathematical and scientific contexts. By elucidating the relationship between a matrix and its characteristic polynomial, this theorem enriches the study of eigenvalue problems and spectral theory, providing essential tools for analyzing linear systems and their underlying structural properties.
It is a testament to the deep connections between algebra and analysis.
The Cayley-Hamilton Theorem stands as a testament to the deep connections between algebra and analysis, showcasing the intricate interplay between algebraic structures and analytical properties in the realm of linear transformations and matrix theory. This profound relationship underscores the unity of mathematical concepts and the synergistic nature of different branches of mathematics, exemplifying the elegance and coherence inherent in the study of mathematical sciences.
The theorem offers a powerful approach to matrix diagonalization and exponentiation.
The Cayley-Hamilton Theorem offers a powerful approach to matrix diagonalization and exponentiation, providing essential tools for transforming and analyzing matrices in various mathematical and engineering contexts. By leveraging the insights derived from this theorem, mathematicians and scientists can streamline the process of diagonalizing matrices and computing matrix exponentials, thereby facilitating advanced applications in fields such as quantum mechanics, signal processing, and numerical analysis.
It has inspired profound developments in mathematical research and applications.
The Cayley-Hamilton Theorem has inspired profound developments in mathematical research and applications, serving as a catalyst for innovative approaches to problem-solving and theoretical exploration in diverse areas of mathematics and its applications. Its far-reaching influence continues to resonate across academic and industrial domains, driving the advancement of mathematical theory and the development of cutting-edge technologies that rely on the foundational principles elucidated by this timeless theorem.
The Cayley-Hamilton Theorem stands as a testament to the enduring legacy of mathematical innovation and the profound impact of algebraic and analytical insights on the advancement of science and technology. Its far-reaching implications underscore the pivotal role of fundamental theorems in shaping the landscape of mathematical sciences and engineering disciplines, serving as a beacon of inspiration for future generations of mathematicians and scientists.
Conclusion
In conclusion, the Cayley-Hamilton Theorem is a fundamental concept in linear algebra and has far-reaching implications in various mathematical disciplines and real-world applications. Understanding its significance in relation to eigenvalues, characteristic polynomials, and matrix representations is crucial for advanced mathematical studies and practical problem-solving. By grasping the 12 essential facts about the Cayley-Hamilton Theorem, mathematicians and enthusiasts alike can deepen their comprehension of this powerful theorem and its wide-ranging impact.
FAQs
What is the significance of the Cayley-Hamilton Theorem?
The Cayley-Hamilton Theorem establishes a profound connection between a square matrix and its characteristic polynomial, providing a powerful tool for solving linear algebraic problems and understanding the behavior of linear systems.
How is the Cayley-Hamilton Theorem applied in real-world scenarios?
The theorem finds applications in various fields, including control theory, signal processing, quantum mechanics, and structural engineering, where it aids in analyzing and manipulating complex systems governed by linear transformations.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
