
The world is full of mysteries, contradictions, and questions that are seemingly impossible to answer. Paradoxes, for instance, are great examples of thoughts that can leave you scratching your head. What is a paradox, anyway? A paradox, sometimes referred to as antimony, is a statement that has a logically sound premise but comes to a conclusion that appears to be senseless, absurd, self-contradictory, or the opposite of the expected outcome. It could be a situation that produces two opposite but entirely possible outcomes. Or, it could be as simple as a sentence that contradicts itself, such as “This statement is a lie”. Paradoxes are some of the most unusual quirks of human logic. To better understand them, we’ve compiled a list of some famous paradoxes that will surely blow your mind.
The Liar Paradox

The liar paradox or liar’s paradox statement is one of the simplest yet most famous paradoxes out there. The statement “this statement is a lie” or “this statement is false” is a paradox because if that statement is indeed a lie, then it would be saying the truth. If the statement is the truth, however, then it would counter the premise that the statement is a lie. This statement contradicts itself and indicates that the statement is both true and false. Weird to think about, isn’t it?
Different forms of this paradox have been around for centuries. The Epimenides paradox, for example, existed since around 600 BC. Epimenides, a semi-mythical Cretan seer and philosopher, famously said that “all Cretans are liars.” This would mean that as a Cretan himself, Epimenides is a liar as well if this sentence were true. If Epimenides is lying when he said that statement, however, then it would follow that Cretans would be truthful — but that would mean that Epimenides, a Cretan, would be lying. This again confirms that Cretans are liars, making the statement true and Epimenides would not be lying. The cycle continues. Scratching your head yet?
Another popular version of the liar paradox is the Pinocchio paradox. In this version, the dilemma arises when Pinocchio says “My nose grows now.” Pinocchio’s nose only grows when he is lying, however, so if the sentence is true, then Pinocchio’s nose will not grow. However, this would mean that Pinocchio is lying, which causes his nose to grow. As Pinocchio’s nose grows now, then Pinocchio would not be lying… which means his nose will not grow, and so on without end. Some have sought solutions to this problem and claim that Pinocchio was not inherently being dishonest — he was simply making a prediction that would turn out to not be true. The prediction that his nose will grow wouldn’t count as a lie, so Pinocchio would not be lying even if he says his nose will grow and it doesn’t.
The Fermi Paradox

With the vast knowledge we have of the observable universe, scientists say that the Sun is a pretty common star and there are billions of stars similar to it in the Milky Way alone. There’s also a good chance that those Sun-like stars have Earth-like planets orbiting around them. It’s also pretty likely that these stars and planets have been around for much longer than our solar system, so the evolution of intelligent life and civilizations more advanced than us would likely be possible. These advanced civilizations may have developed interstellar travel already or at least launched probes to study other planets from far away. However, even with the likelihood of all of these circumstances, why hasn’t anyone made contact with us yet? Shouldn’t their presence be obvious to us by now?
The Fermi paradox presents this problem. If Earth is just one of the billions of planets that have similar conditions, why is it that sentient life seems to be unique to us? The paradox takes its name from the Italian-American physicist Enrico Fermi. While he wasn’t the first one to raise the problem, the paradox has ties to his name because of his conversation with fellow physicists Edward Teller, Herbert York, and Emil Konopinski in 1950. In this conversation, while they were talking about UFO sightings and faster-than-light travel, Fermi reportedly asked, “But where is everybody?”
The conflict between the scientific estimates that sentient life is likely common in the Universe and the fact that we don’t have any solid evidence of sentient life on other planets still baffles scientists to this day. Some have tried to explain this paradox by arguing that intelligent life outside of Earth is extremely rare and civilizations like these have short lifetimes. Others have suggested that alien life could be so alien that it’s completely unrecognizable to us.
The Unexpected Hanging Paradox

This paradox follows a condemned prisoner that a judge sentenced to death by hanging. The judge tells the prisoner that the executioner will hang him at noon on a weekday in the following week. He also told the prisoner that the day of the execution will be a surprise. Thus, the prisoner will not know the exact day of his execution. He will only know the day of his hanging when the executioner comes knocking on his cell door.
The prisoner, upon hearing his punishment, reflected on it and concluded that he’ll be able to escape his execution. Because the execution will happen on a weekday, he argued that his execution can’t be on a Friday because the judge told him that the day will be a surprise to him. Therefore, when Thursday passes and he’s still alive, he will know that the execution will be on Friday. This means that the day of the hanging won’t come as a surprise to him anymore.
After drawing the conclusion that the day of his execution can’t occur on a Friday, he reasons further and states that his execution cannot be on a Thursday either. That’s because when he’s still alive when Wednesday noon passes, then the hanging must be on a Thursday, given that he already ruled out the possibility of a Friday execution. Therefore, a Thursday execution will not be a surprise as well. Using the same line of reasoning, he further argued that the execution also won’t occur on a Wednesday, a Tuesday, or a Monday. After making his arguments, he happily went back to his cell. He was confident that the surprise hanging will not happen at all.
When the week of the execution came, the executioner knocked on the prisoner’s cell door on a Wednesday. This came as a surprise to the prisoner, who was confident that the execution wouldn’t happen at all. Thus, what the judge told him eventually came true.
The unexpected hanging paradox has a lot of other versions, such as those involving a surprise test or pop quiz. Many philosophers also attempted to resolve this paradox, but there is no unanimous agreement on its nature and resolution. Some even say that it remains a significant problem in philosophy to this day, and that’s why it’s among the most famous paradoxes!
Schrödinger's Cat Paradox

If you’re a fan of science, particularly physics and quantum mechanics, then you likely have already heard of Schrödinger’s cat. This thought experiment is one of the famous paradoxes that have a profound impact on science.
In this popular paradox, imagine a cat trapped inside a box. Within that same box, there’s also an apparatus that will shatter a poison-filled flask if it detects radioactivity (such as when a single atom decays). When the flask shatters, the poison will kill the cat inside the box.
After a while, the flask may or may not have shattered, and the cat may or may not be dead. Until an observer comes along and opens the box, the cat is in a superposition. This would mean that it’s both alive and dead at the same time. When someone opens the box and takes a look, however, the cat will only be one or the other. It would be either dead or alive and not both at the same time.
The Austrian-Irish physicist Erwin Schrödinger first devised this thought experiment in 1935, in a conversation with Albert Einstein. This scenario represents the current leading interpretation of quantum mechanics, wherein a quantum system remains in superposition until scientists measure or observe them. For example, some subatomic particles (such as electrons) behave as both a particle and a wave. This is much like how the cat is both alive and dead at the same time. Upon observation, however, the electrons act as either particles or waves, never both at the same time. This means that the presence of an external observer collapses a quantum system into just one state. Because of its implications on quantum mechanics, the paradox of Schrödinger’s cat continues to be a significant part of scientific discussions to this day.
The Interesting Number Paradox

This paradox is among the silliest and most whimsical of all these famous paradoxes. In this paradox, suppose that you have to classify all natural numbers as either “interesting” or “not interesting”. The paradox postulates that every natural number is interesting in some way, even if you don’t find it interesting. Once you find a number that doesn’t seem interesting, then it becomes interesting by virtue of it becoming the first number that is not interesting. This then creates a contradiction — a paradox. It’s a rather silly paradox at that because of the sheer subjectivity of the concept of “interestingness”.
The Interesting Number Paradox famously came up in a conversation between mathematicians G. H. Hardy and Srinivasa Ramanujan about interesting numbers. In the conversation, Hardy reportedly stated that the number 1729 of the taxicab that he’d ridden was rather dull. However, Ramanujan promptly replied that the number was interesting because it is the smallest number that is the sum of two cubes in two different ways. The number 1729, later on, became famous as the “taxicab number” or the “Hardy-Ramanujan number”.
Nathaniel Johnston, a quantum-computing researcher, sought to resolve this paradox by defining an “interesting” number objectively. He defined a number as interesting if it appears on the On-Line Encyclopedia of Integer Sequences (OEIS), which contains thousands of integer sequences. Using this definition, Johnston found in 2009 that the first “uninteresting number”, or the first number that didn’t appear on the OEIS, was 11,630.
The Crocodile Paradox

This is among the famous paradoxes that are in line with the Liar Paradox. Suppose that a crocodile grabs a young child from a riverbank. The child’s parent then asks the crocodile to return the child safely, but the crocodile replies that he will return the child only if the parent can correctly guess if he will safely return the child or not.
Now, if the parent correctly guesses that the crocodile will return the child safely, then there will be no problem. If the parent is wrong, then the crocodile will keep the child. The paradox then arises if the parent guesses that the crocodile will not return the child. If this happens and the crocodile returns the child, then this will contradict the parent’s answer and the crocodile will be breaking his promise. Furthermore, if the crocodile does not return the child, then the parent will have correctly guessed the answer and the crocodile should then return the child safely. However, this scenario would then also result in the parent being wrong about the prediction. Therefore, there wouldn’t be any justifiable solution for what the crocodile will do.
The Crocodile Paradox dates back to ancient Greece. People in the Middle Ages even used “crocodilite” to refer to a similar dilemma wherein your words are used against you.
The Lottery Paradox

This paradox originated from Henry E. Kyburg Jr. in 1961. Let’s say you buy a lottery ticket just for fun. Assume that there are at least ten million tickets and that the lottery is fair with exactly one winning ticket. Your chances of winning would then be one in 10 million, which you know isn’t likely to happen. It’s therefore perfectly reasonable to assume that your ticket will lose. It’s also perfectly reasonable to assume that the next ticket will lose, too. That goes for the next ticket as well, and the next, and the next, and so on. Your belief that every ticket bought from the lottery will lose will be completely justified by the odds.
Even though you’re perfectly reasonable in thinking that every ticket will lose, you know that one ticket will win. The problem is this: why is it still reasonable to assume that every ticket will lose, even if you know that one will win? This problem has been around since the early 1960s, and it has opened up a lot of discussions regarding knowledge, rationality, and other philosophical concepts.
Achilles and the Tortoise Paradox

The Greek philosopher Zeno of Elea, who lived in the 5th century BC, is popular for introducing many famous paradoxes. One great example of these is the Paradox of Achilles and the Tortoise. In this paradox, the great mythological warrior Achilles is in a footrace with a tortoise. Because tortoises are notoriously slow, he agrees to give the tortoise a head start. Let’s say the tortoise gets a head start of a hundred feet before Achilles starts running.
Obviously, when Achilles runs, he’ll run much faster than the tortoise and will eventually reach the tortoise’s starting point of a hundred feet. However, by the time Achilles reaches the hundred-foot marker, the tortoise will have walked about 10 feet further. It will take Achilles a bit more time to reach that point. By that time, the tortoise will have walked a foot further again. Although the distance will become smaller and smaller, Achilles will have to infinitely play catch up with the slow tortoise that’s always moving ahead. He can never overtake the tortoise because he will always have some distance left to run to reach somewhere the tortoise has been.
Now, practically speaking, it isn’t that hard to outrun a tortoise in real life. However, practicality is not the point of this famous paradox. Instead, this paradox only exists to provide some insight into one of the most fundamental and hardest-to-grasp aspects of mathematics — infinity. Zeno’s Achilles and the Tortoise Paradox tackles the concept that there is an infinite distance between two finite numbers. For example, between the numbers one and zero, there exists an infinite number of smaller and smaller numbers (or distances) such as 0.1, 0.01, 0.001, 0.0001, and the list goes on. It’s such a mind-blowing concept to think about!
The Dichotomy Paradox

Like Achilles and the Tortoise, this is another one of Zeno’s famous paradoxes. In this paradox, imagine that you’ll be walking to reach a certain point down a street — but for you to reach your destination, you would have to walk halfway there. Furthermore, before you walk halfway to the destination, you’d have to walk a quarter of the way there. To reach a quarter of the way there, you’d also have to walk an eighth of the way there, which would then require you to walk a sixteenth of the way there, and so on without end.
This would ultimately mean that to reach a certain point, you would have to do an infinite number of smaller and smaller tasks, which Zeno deems utterly impossible. In this paradox, no matter how small your starting point is, you can always divide the task into smaller and smaller divisions. Therefore, the only way for your starting point to not be halved is to travel no distance at all.
This ultimately concludes with Zeno saying that you cannot travel any finite distance and motion is just plain impossible. Of course, we can see that things do move, but Zeno maintains that things are not as they appear and that motion is merely an illusion. Definitely one of the famous paradoxes that will leave you scratching your head!
The Fletcher’s Paradox

This paradox is yet another mind-boggling work from Zeno, which begins with an arrow-maker or fletcher. Say a fletcher fires one of his arrows into the air. To prove that the arrow is indeed moving, it needs to continuously reposition itself from the place where it has originated and to any place where it isn’t. However, Fletcher’s Paradox states that the arrow, all throughout its trajectory flight, is not moving.
During the arrow’s flight, any instance of real duration is nonexistent. Simply put, the arrow cannot move to anywhere it currently isn’t because there is no time given for it to happen. It also has no capacity to move where it currently is, because it’s already in that place. So, for that snapshot in time, the arrow is only stationary. The paradox further states, however, that time is a series of instants, which includes a single panel where the arrow is stationary. With that, we can deduce that the arrow must indeed be stationary through the shot — even when it apparently isn’t.
The Raven Paradox

The Raven Paradox is also known as Hempel’s Paradox, which is named after a German logician who created the concept in the 1940s. The concept of the paradox is rather straightforward compared to the other statements depicted so far. Hempel postulates a true statement: all ravens are black. This is then supported by a logical contrapositive concept, which means a negative and contradictory statement. Now, we can say that everything that is not black is not a raven.
The idea may seem ludicrous and unnecessary, especially considering the statement already provided that all ravens are indeed black. So, whenever we see a black raven, it supports that everything that isn’t black isn’t a raven. This then translates to other concepts, such as an orange — if an apple is not black, then it isn’t a raven.
So, how is this a paradox? Hempel essentially proves that seeing an orange is already evidence in itself, particularly when it comes to the true statement depicting that ravens are black. Unfortunately, the implications are endless — what else can you pull from this paradox?
Galileo’s Paradox of the Infinite
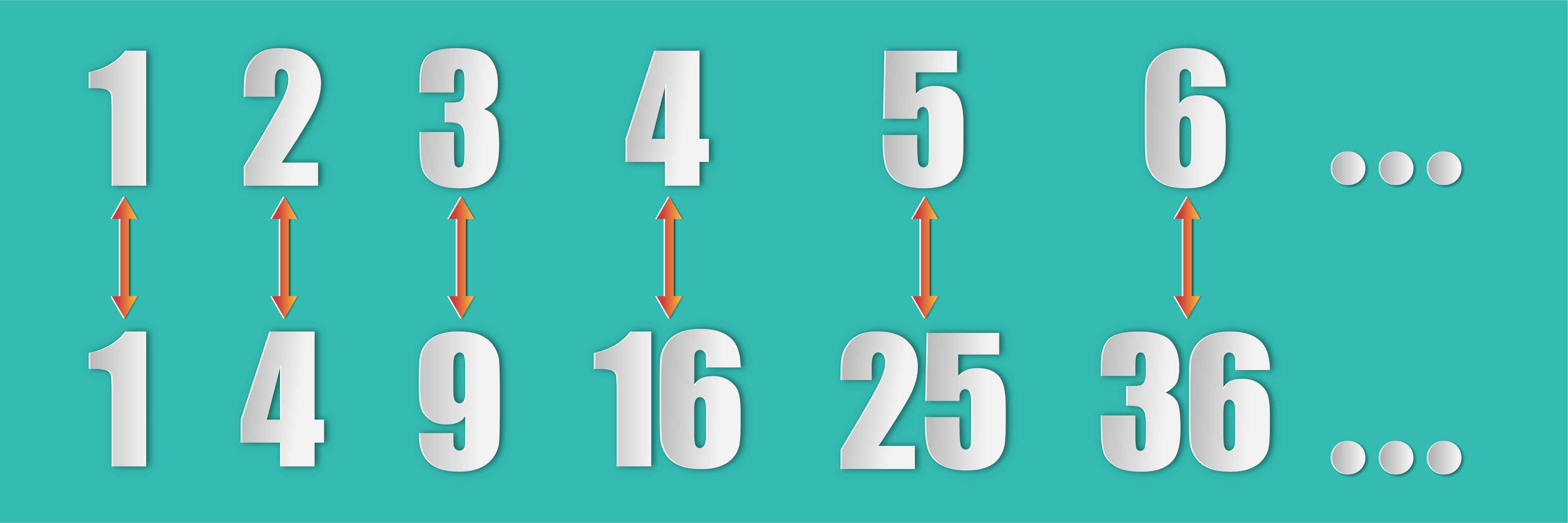
The renowned Italian polymath Galileo Galilei introduced one of the most famous mathematical paradoxes in his final written work. In his work Discourses and Mathematical Demonstrations Relating to Two New Sciences (1638), he discussed his Paradox of the Infinite.
Suppose there are two sets of numbers. One set contains all square numbers such as 1, 4, 9, 16, 25, and so on until infinity. The other set contains numbers that are not squares such as 2, 3, 5, 6, 7, 8, and so on until infinity. When you combine these two sets, you will end up with a set with more numbers than just the two sets separately. The total number of squares will surely be less than all the numbers together. However, each positive number only has exactly one square and cannot possibly contain more numbers than the other set.
This paradox left Galileo with the conclusion that concepts such as more, less, and equal only apply to finite sets of numbers. They don’t apply to infinite sets. Later works by German mathematician Georg Cantor then drew the conclusion that some infinite sets are larger than others.
The Unstoppable Force Paradox

You probably already have heard of this paradox because it’s certainly one of the most recognizable famous paradoxes out there. The unstoppable force or irresistible force paradox goes like this: “What happens when an unstoppable force meets an immovable object?” Will the immovable object be moved, or will the unstoppable force be stopped?
This classic paradox involves two indestructible and incompatible things, which makes it complex and mind-boggling. If there is such a thing as an unstoppable force, it should follow that there is no such thing as an immovable object. This is true for the reverse. However, both exist in this paradox, so there’s no easy answer to the question.
Like many famous paradoxes, there are many versions of the unstoppable force paradox. One example from China is a story that dates back to the 3rd century BC. In this story, a merchant was trying to sell a spear and a shield. When people asked him how good his spear was, he answered that it could pierce any shield. Then, when people asked him how good his shield was, he replied that it was so strong that it could block attacks from any spear. However, one person came and asked what would happen if he took the merchant’s spear and struck the shield with it. The merchant could not answer. This paradox gave rise to the idiom of “zìxīang máodùn” (自相矛盾) which roughly translates to “from each-other spear shield” or “self-contradictory”.
The Boy or Girl Paradox

This paradox’s original version dates back to 1959 when Martin Gardner introduced it in his “Mathematical Games” column in the October 1959 issue of Scientific American. Gardner originally called it “The Two Children Problem”.
The paradox involves two families: Mr. Jones’s family and Mr. Smith’s family. Mr. Jones has two kids, the older of which we know to be a girl. What’s the probability that the younger child is a girl as well? It should be obvious that the answer is ½ because the younger child could just either be a boy or a girl. Furthermore, the odds of giving birth to a boy and a girl are essentially equal.
Mr. Smith, on the other hand, also has two kids. At least one of them is a boy. What is the probability that both children are boys? Surprisingly, it’s ⅓! That’s because there are actually four possible combinations of children in a two-child family: both boy children (MM), both girls (FF), an older boy and a younger girl (MF), and an older girl and a younger boy (FM). We just know that one of Mr. Smith’s kids is a boy, which only leaves us with the possibility of Mr. Smith’s children being both boys (MM), just the older child being a boy (MF), and just the younger child being a boy (FM). The odds of those combinations are equal, making it ⅓!
The ambiguity of the question changed the probability. Even today, the paradox continuously generates considerable controversy. Mind-blowing, isn’t it? It gets even more complicated with other versions of the problem. The pr when the boy child has a name or if he were born on a specific day of the week.
Sorites Paradox or the Paradox of the Heap

The sorites paradox, also known as the paradox of the heap, is essentially a concept that happens from what are called vague predicates. The concept usually involves heaps of sand, where the grains are removed individually.
Considering the postulation that removing a single grain cannot turn the sand heap into a non-heap, the paradox then lies in an idea: what happens if the removal happens multiple times, just enough to make sure that only a single grain remains? Does that make a single grain still a heap? If it isn’t, at what point did it change into a non-heap? What do you suppose is the answer?
The Potato Paradox

This paradox is another one of the famous paradoxes that involve the beauty of mathematics. In this paradox, suppose that a farmer has a sack of potatoes, say 100 lbs of it. He discovers that these potatoes comprise 99% water and 1% solids. The farmer then leaves the potatoes outside to dry under the heat of the sun for a day. When the next day came, the potatoes dried to just about 98% water, but to the farmer’s shock, the potatoes only had a weight of 50 lbs. How did this happen with just a 1% drop in water content?
Given that the 100 lbs of potatoes are 99% water, then the weight of the water must be 99 lbs. Also, the weight of the solids must be 1 lb because it makes up just 1% of the 100 lbs. This makes the water-solid ratio 1:99. Once the potatoes have dried to just 98% water, however, the solid compounds now make up 2% of the potatoes’ weight. This now gives a new ratio of 2:98 or 1:49. The solids still retain their original weight of 1 lb, so given the new ratio, the water must now have a weight of just 49 lbs. This makes the new total weight of the potatoes just 50 lbs! This result would still hold true as long as you double the non-water concentration. For instance, reducing the water content of the potatoes from 99.999% still would result in halving the potatoes’ original weight.
The Potato Paradox is a type of veridical paradox. This means that despite the seemingly absurd result, the theory is logical and perfectly reasonable.
The Teletransportation Paradox

The Teletransportation Paradox is another one of the most interesting famous paradoxes. It first appeared in published form in the 1984 book Reasons and Persons by British philosopher Derek Parfit, but similar questions existed long before then. Imagine that there’s a “teletransporter” machine on Earth. It puts you to sleep, records your molecular composition, breaks you down into your constituent atoms, and relays that information to somewhere on Mars at the speed of light.
At the receiving end on Mars, a machine recreates your body atom by atom down to the last detail. When that body wakes up, it will have all your memories and all the parts that make you who you are. It even has the smallest of cuts from when you shaved that morning. Now, is the person on Mars still the same person as the one who entered the teletransporter on Earth? Is it still the same you or did you cease to exist when the teletransporter destroyed your physical body?
You could say that your replica on Mars is still the same you and that the teletransporter was just a way for you to travel. However, to make things more complicated, let’s say the teletransporter became faulty over time. It failed to destroy your original body on Earth. Thus, the machine now just made an exact replica of you on Mars. The replica would have the same memories as you and can claim to be you. It even remembers entering the teletransporter on Earth to travel to Mars! Your Martian self will identify itself with you. Which one is the real you in this case?
One related paradox about identity is the Ship of Theseus, which dates back to ancient Greece. In this paradox, the problem is this: If you replace the parts of a ship one by one until it no longer has its original components, is it still the same ship? It’s a mind-blowing and a little concerning problem to think about!
The Grandfather Paradox

Time travel has always been a favorite subject of many. The entire concept of traveling back in time continues to spark debate in the scientific community. Much confusion and theories arise, and all for good reason. Time, after all, is a tricky concept to grasp. A more pressing question, however, continues to fuel the imagination of countless people all over the world — is time travel even possible?
The French journalist Rene Barjavel spent most of his time pondering on the concept of time travel. In 1943, he proposed an idea: what if a man goes back in time, particularly before his parents were born, and then proceeds to kill his grandfather?
The death of the grandfather means one of the man’s parents will never see the light of the day. The man himself also never would have existed. That would mean that there will be nobody who will go back in time to murder the grandfather.
This paradox not only sparks discussion among the scientific community. People who study philosophy also join in on the fun, along with fans of the film trilogy Back to the Future. Other people postulate that time travel can be possible through a parallel universe theory, where time travelers can end up creating a separate timeline that branches off the already existing one. There are also other versions of the Grandfather Paradox. One version has this problem: What would happen if you go back in time and kill Adolf Hitler? Definitely among the famous paradoxes that are interesting to think about!
The Bootstrap Paradox

The Bootstrap paradox is yet another play in time. It essentially questions how something that is taken from the future, to be placed in the past, can never come to exist. It’s a common idea used by the science fiction realm, heavily decorating book plots, film concepts, and other more prominent ideas. The most renowned and memorable example of the Bootstrap is The New Time Travellers, which was written by Professor David Toomy.
Let’s put it this way. Say that William Shakespeare’s Romeo and Juliet was taken from a bookstore by the time traveler. The time traveler then goes back in time to give the book to Shakespeare. Shakespeare then pays to make copies of the book, claiming it as his own work. Centuries pass, and Romeo and Juliet continues to be printed, produced, and read by countless people. Eventually, it finds its way back to the bookstore, where the time traveler takes it and brings it back to Shakespeare. The question now stands — who actually wrote the drama?
The Monty Hall Problem

To cap off this list of famous paradoxes, here’s another fun paradox: the Monty Hall Problem. The paradox takes its name from the American television game show Let’s Make a Deal, whose original host was Monty Hall. Statistician Steve Selvin first described the problem in his 1975 letter to the scientific journal The American Statistician. It also rose to popularity in 1990 because of Marilyn vos Savant’s “Ask Marilyn” column in Parade magazine.
In the Monty Hall Problem, you’re in a game show and you have to choose among three different doors. There is a brand-new car behind one door and goats behind the other two doors. Let’s say that you pick Door #1. The host, who knows where the goats are and where the car is, opens Door #3 to reveal a goat. He then offers you a choice to switch to Door #2. If you want to win the car, should you make the switch to Door #2?
Marilyn vos Savant stated in her column that the player should make the switch. According to her, it increases the chances of winning the car. She wrote that when you make the initial choice, your chance of winning a car is ⅓. When the host opens the door with a goat and offers you the choice to switch, making the switch would surprisingly bring your chances up to ⅔. How does this happen?
When you make your initial decision of Door #1, the chances of you winning your dream car would be ⅓. This means that there will be a ⅔ chance that the car is behind some other door. That would be either Door #2 or Door #3 in this case. Since you know that Door #3 contains a goat, the odds remain the same. There is a ⅔ chance that Door #2 contains the car. If you don’t switch, you still retain your ⅓ chance of winning the car. Although you may think that switching does nothing to increase your odds of winning, it actually increases your chances! Mind-blowing, isn’t it?
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.


