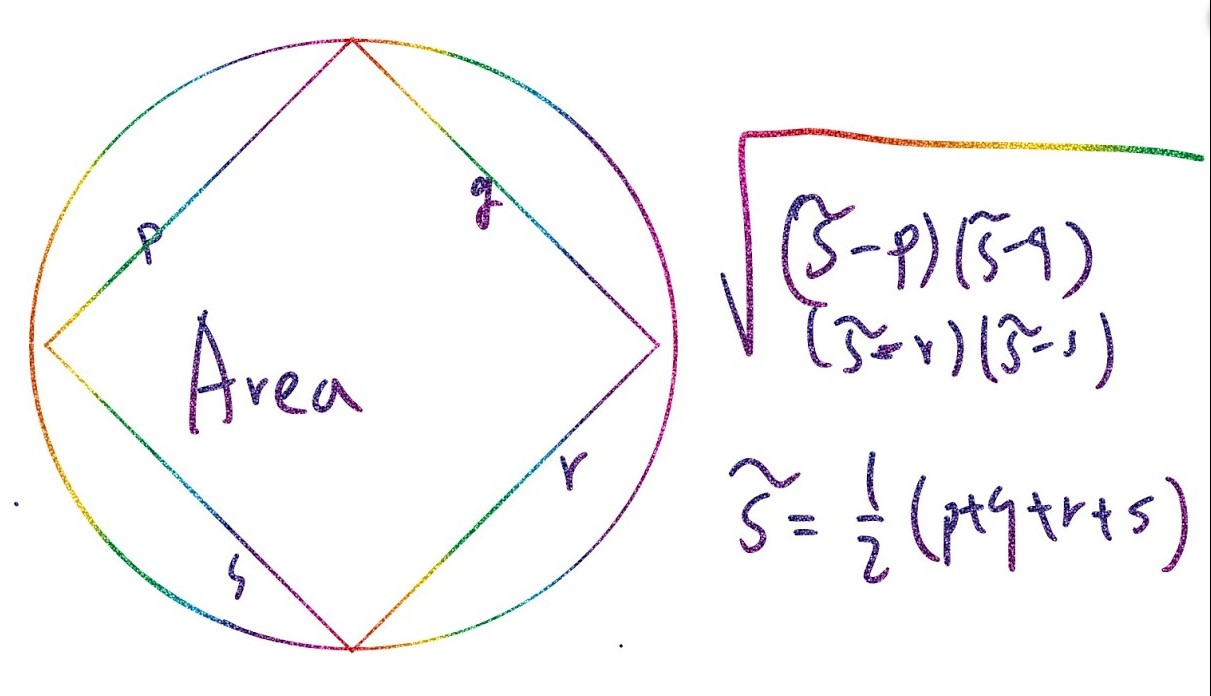
Brahmagupta's Formula is a significant concept in the field of mathematics, particularly in the realm of geometry. Named after the renowned Indian mathematician and astronomer Brahmagupta, this formula holds great importance in calculating the area of a cyclic quadrilateral. Understanding the intricacies and applications of this formula can provide valuable insights into the fundamental principles of geometry and its practical implications.
In this article, we will delve into 10 essential facts about Brahmagupta's Formula, shedding light on its origins, mathematical significance, and real-world applications. From its historical roots to its relevance in modern mathematics, each fact will unravel a unique aspect of this formula, offering a comprehensive understanding of its importance and utility. Whether you are a mathematics enthusiast, a student seeking to expand your knowledge, or simply curious about the wonders of mathematical concepts, exploring these facts will undoubtedly enrich your understanding of Brahmagupta's Formula and its enduring impact on the world of mathematics.
Key Takeaways:
- Brahmagupta’s Formula is a versatile and practical theorem that helps calculate the area of cyclic quadrilaterals without relying on trigonometric functions, making it a valuable tool for geometric problem-solving.
- Brahmagupta’s Formula, formulated by an ancient Indian mathematician, continues to inspire scholars and find applications in diverse fields such as engineering and architecture, showcasing the enduring legacy of ancient mathematical wisdom.
Brahmagupta's Formula: A Mathematical Marvel
Brahmagupta's Formula, a significant theorem in mathematics, holds a prominent place in the realm of geometry. This formula provides a means to calculate the area of a cyclic quadrilateral, a polygon whose vertices lie on the circumference of a circle. Let's delve into 10 intriguing facts about this remarkable mathematical concept.
Brahmagupta, an Ancient Indian Mathematician
Brahmagupta, an influential mathematician and astronomer in ancient India, formulated this theorem in the 7th century. His profound contributions to mathematics continue to inspire scholars and students worldwide.
The Formula's Fundamental Components
Brahmagupta's Formula involves the lengths of the sides of the cyclic quadrilateral and a crucial element known as the semiperimeter. Understanding these components is essential for applying the theorem effectively.
A Versatile Theorem
This formula is not limited to specific types of quadrilaterals; rather, it can be applied to a wide array of cyclic quadrilaterals, showcasing its versatility and practicality in geometric calculations.
The Formula's Geometric Significance
Brahmagupta's Formula provides a means to determine the area of a cyclic quadrilateral without relying on trigonometric functions, offering a geometric approach to solving such mathematical problems.
A Pillar of Geometric Problem-Solving
Mathematicians and problem solvers frequently utilize Brahmagupta's Formula to tackle diverse geometric challenges, highlighting its significance in the field of mathematics.
The Formula's Influence on Modern Mathematics
Brahmagupta's contributions have left an indelible mark on modern mathematics, with his formula serving as a cornerstone in the study of geometric theorems and their applications.
Applications Beyond Mathematics
The principles underlying Brahmagupta's Formula extend beyond the realm of mathematics, finding applications in diverse fields such as engineering, architecture, and computer graphics.
A Testament to Ancient Mathematical Ingenuity
Brahmagupta's Formula stands as a testament to the ingenuity of ancient mathematicians, showcasing their advanced understanding of geometric concepts and their practical implications.
The Formula's Enduring Legacy
Centuries after its inception, Brahmagupta's Formula continues to captivate mathematicians and learners, perpetuating its legacy as a fundamental theorem in the realm of geometry.
Brahmagupta's Formula, with its rich historical significance and enduring relevance, remains a cornerstone of geometric theorems, embodying the timeless wisdom of ancient mathematical scholars.
Conclusion
Brahmagupta's Formula has left an indelible mark on the field of mathematics, revolutionizing the way we approach and solve complex mathematical problems. Its elegant simplicity and profound implications have solidified its status as a cornerstone of algebraic understanding. By delving into the depths of this formula, we have uncovered its far-reaching influence and timeless relevance in the realm of mathematical sciences. As we continue to explore the boundless frontiers of mathematics, the legacy of Brahmagupta's Formula will undoubtedly endure, inspiring and guiding future generations of mathematicians and problem solvers.
FAQs
What is the significance of Brahmagupta's Formula?
Brahmagupta's Formula holds immense significance in the field of mathematics as it provides a fundamental method for calculating the area of a cyclic quadrilateral, thereby contributing to the broader understanding of geometric principles and algebraic concepts.
How does Brahmagupta's Formula impact modern mathematics?
Brahmagupta's Formula continues to impact modern mathematics by serving as a foundational tool for solving geometric problems and advancing algebraic techniques. Its applications extend to various fields, including engineering, physics, and computer science, making it a vital component of contemporary mathematical research and innovation.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
