28 Facts About Homotopy

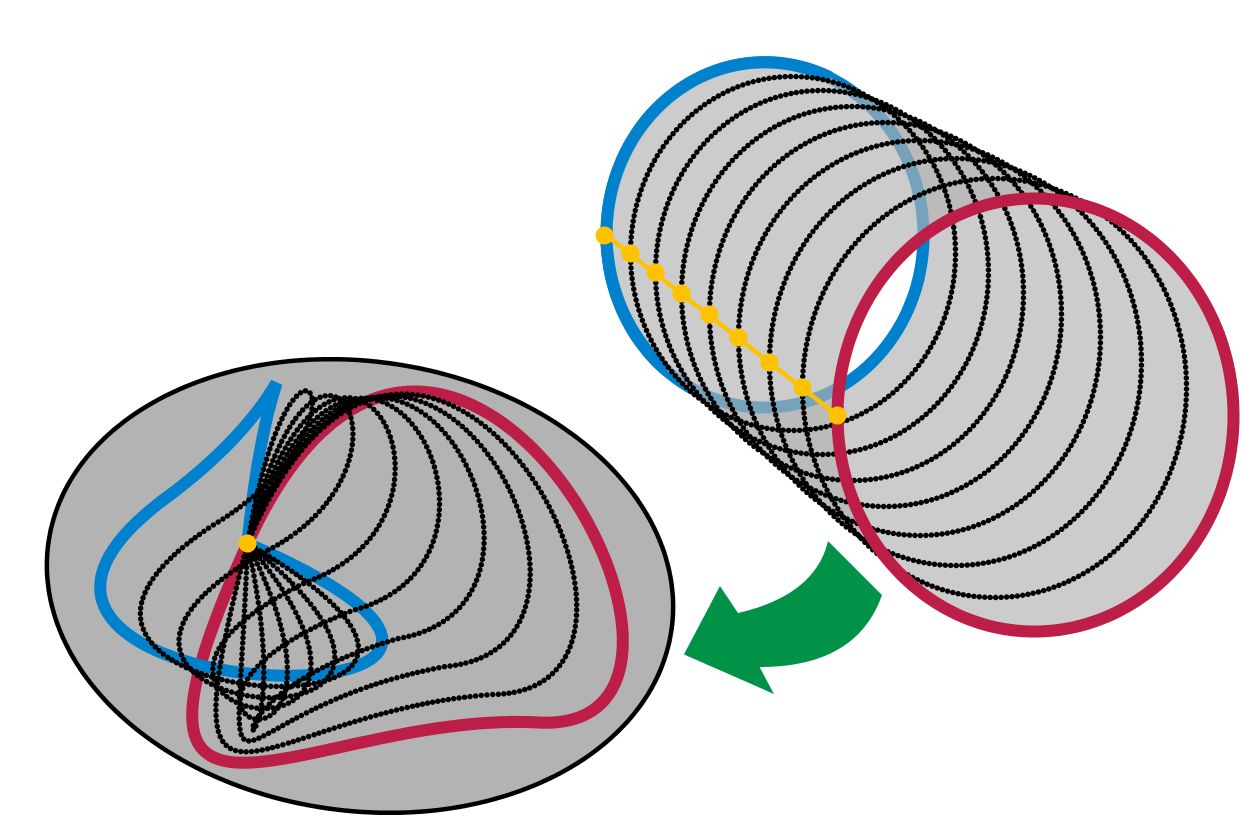
What is Homotopy?

Homotopy is a concept in topology, a branch of mathematics. It deals with the idea of deforming one shape into another without cutting or gluing. This concept helps mathematicians understand the properties of spaces that remain unchanged under continuous transformations.

1. Homotopy comes from the Greek words "homoios" (similar) and "topos" (place).
2. Two shapes are homotopic if one can be continuously deformed into the other.
3. Homotopy equivalence is a relation between two topological spaces that can be transformed into each other by continuous maps.
4. Homotopy groups are algebraic structures that classify topological spaces based on their homotopy properties.
5. The fundamental group is the first homotopy group, representing loops in a space starting and ending at the same point.

Applications of Homotopy

Homotopy isn't just a theoretical concept; it has practical applications in various fields. From computer graphics to robotics, understanding homotopy can be quite useful.

6. Computer graphics use homotopy to morph shapes smoothly.
7. Robotics applies homotopy to plan paths for robots, avoiding obstacles.
8. Data analysis utilizes homotopy to understand the shape of data in high-dimensional spaces.
9. Physics employs homotopy in studying the properties of space-time and field theories.
10. Biology uses homotopy to model the folding of proteins and other biological structures.

Homotopy in Algebraic Topology

Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. Homotopy plays a crucial role in this field.

11. Algebraic topology uses homotopy to classify spaces up to homotopy equivalence.
12. Homotopy groups help in understanding the higher-dimensional holes in a space.
13. Homology and cohomology theories are related concepts that complement homotopy in algebraic topology.
14. Spectral sequences are tools in algebraic topology that use homotopy to solve complex problems.
15. Fibrations and fiber bundles are structures in algebraic topology that involve homotopy.

Famous Theorems Involving Homotopy

Several important theorems in mathematics involve homotopy. These theorems provide deep insights into the structure of topological spaces.

16. The Homotopy Extension Property allows extending a homotopy defined on a subspace to the whole space.
17. The Whitehead Theorem states that a map between CW complexes is a homotopy equivalence if it induces isomorphisms on all homotopy groups.
18. The Hurewicz Theorem connects homotopy groups with homology groups.
19. The Freudenthal Suspension Theorem relates the homotopy groups of a space to those of its suspension.
20. The Blakers-Massey Theorem provides conditions under which a map induces an isomorphism on homotopy groups.

Homotopy in Modern Mathematics

Homotopy continues to be an active area of research in modern mathematics. New developments and discoveries keep emerging, expanding our understanding of this fascinating concept.

21. Homotopy type theory is a new branch of mathematics that combines homotopy theory and type theory.
22. Derived algebraic geometry uses homotopy to study geometric objects in a more flexible way.
23. Homotopy theory has connections with category theory, another abstract branch of mathematics.
24. Stable homotopy theory studies homotopy groups in a stable range, providing deep insights into the structure of spaces.
25. Homotopy colimits and limits are constructions in category theory that generalize the notion of colimits and limits using homotopy.

Fun Facts about Homotopy

Homotopy isn't just for mathematicians. Some fun and quirky facts make this concept even more interesting.

26. Homotopy can be visualized using animations that show one shape transforming into another.
27. Rubber sheets and elastic bands are often used as analogies to explain homotopy.
28. Homotopy has inspired artists to create sculptures and artworks that explore continuous transformations.

Final Thoughts on Homotopy

Homotopy, a fascinating concept in mathematics, connects shapes and spaces in ways that might seem magical. It helps mathematicians understand how different shapes can transform into each other without tearing or gluing. This idea has applications in various fields, from computer science to physics. By studying homotopy, researchers can solve complex problems and gain insights into the fundamental nature of space and form. It's a powerful tool that continues to inspire and challenge those who delve into its depths. Whether you're a student, a professional, or just curious, exploring homotopy can open up a world of possibilities and deepen your appreciation for the beauty of mathematics. Keep questioning, keep exploring, and who knows what new discoveries you might make!