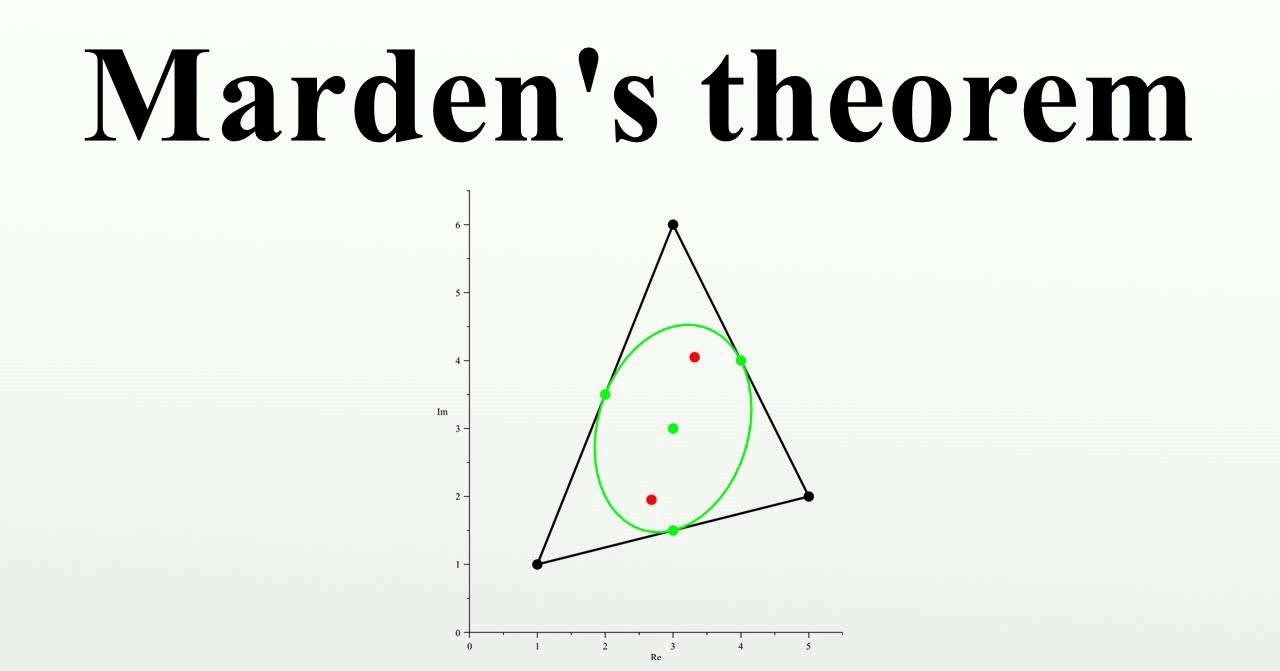
Marden's Theorem is a captivating concept in the realm of mathematics, offering profound insights into the properties of complex numbers and their geometric interpretations. This theorem, named after the distinguished mathematician James Marden, holds a significant place in the study of polynomials and their roots. Understanding Marden's Theorem unveils a world of connections between algebra and geometry, shedding light on the intricate relationships between seemingly disparate mathematical domains.
In this article, we will delve into the depths of Marden's Theorem, unraveling its intricacies and unveiling its practical applications. From its historical origins to its modern-day relevance, we will explore ten compelling facts that illuminate the significance of Marden's Theorem. Join us on this mathematical journey as we uncover the beauty and utility of this theorem, gaining a deeper appreciation for its elegance and mathematical prowess.
Key Takeaways:
- Marden’s Theorem connects polynomial roots to their geometric locations, helping mathematicians understand their behavior and relationship to the coefficients. It’s like a treasure map for understanding complex equations!
- This theorem is like a secret code that unlocks the mysteries of polynomial roots, inspiring new research and enhancing our understanding of complex functions. It’s like a key to a hidden mathematical treasure chest!
Marden's Theorem: Unveiling the Mysteries of Polynomial Roots
Marden's Theorem, a remarkable result in the field of complex analysis, offers profound insights into the behavior of polynomial roots. Let's delve into the fascinating world of Marden's Theorem and unravel its significance.
Marden's Theorem Sheds Light on Polynomial Roots
Marden's Theorem provides a captivating perspective on the distribution of roots of a polynomial in the complex plane. By examining the locations of these roots, mathematicians can gain valuable understanding of the polynomial's characteristics and behavior.
It Relates Polynomial Roots to the Coefficients
This theorem establishes a profound connection between the roots of a polynomial and its coefficients, offering a powerful tool for analyzing and interpreting the properties of polynomial equations.
Marden's Theorem Offers Geometric Insights
By leveraging geometric concepts, Marden's Theorem enables mathematicians to visualize the distribution of polynomial roots in the complex plane, leading to deeper comprehension of their spatial arrangements.
It Unveils the Relationship Between Roots and Critical Points
Marden's Theorem illuminates the intricate relationship between the roots of a polynomial and its critical points, providing a comprehensive framework for studying the behavior of complex functions.
Marden's Theorem Empowers Analytical Investigations
This theorem serves as a cornerstone for conducting analytical investigations into the distribution and behavior of polynomial roots, offering valuable tools for mathematicians and researchers.
It Facilitates Advanced Mathematical Analyses
With its profound implications, Marden's Theorem facilitates advanced mathematical analyses, empowering scholars to explore the intricate interplay between polynomial roots and their properties.
Marden's Theorem Inspires Further Research
The profound insights offered by Marden's Theorem continue to inspire further research and exploration in the realms of complex analysis and polynomial equations, driving the advancement of mathematical knowledge.
It Enhances Understanding of Complex Functions
By shedding light on the distribution of polynomial roots, Marden's Theorem enhances our understanding of complex functions and their intricate behavior in the complex plane.
Marden's Theorem: A Cornerstone of Mathematical Theory
Marden's Theorem stands as a cornerstone of mathematical theory, offering profound insights into the behavior of polynomial roots and inspiring new avenues of exploration in the realm of complex analysis.
Marden's Theorem, a remarkable result in the field of complex analysis, offers profound insights into the behavior of polynomial roots. Let's delve into the fascinating world of Marden's Theorem and unravel its significance.
Conclusion
In conclusion, Marden's Theorem is a powerful and elegant concept that has far-reaching implications in the field of mathematics. Its ability to provide a geometric solution to complex problems involving roots of polynomials is truly remarkable. By uncovering the relationship between the roots of a polynomial and the vertices of a triangle, Marden's Theorem has opened up new avenues for exploration and problem-solving in various mathematical disciplines. Its applications extend beyond pure mathematics, impacting fields such as engineering, physics, and computer science. As we continue to delve deeper into the intricacies of Marden's Theorem, we are certain to unearth even more profound insights and practical applications.
FAQs
What is Marden's Theorem?Marden's Theorem is a fundamental result in mathematics that establishes a connection between the roots of a polynomial and the vertices of a triangle. It provides a geometric approach to understanding the behavior of complex polynomial functions and has applications in various mathematical and scientific domains.
How is Marden's Theorem used in practical applications?While Marden's Theorem originates from pure mathematics, its applications extend to practical fields such as engineering, physics, and computer science. It provides a powerful tool for analyzing and solving problems related to polynomial equations, offering insights that have real-world implications.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.


