40 Facts About Chebyshev Polynomials

What are Chebyshev Polynomials?

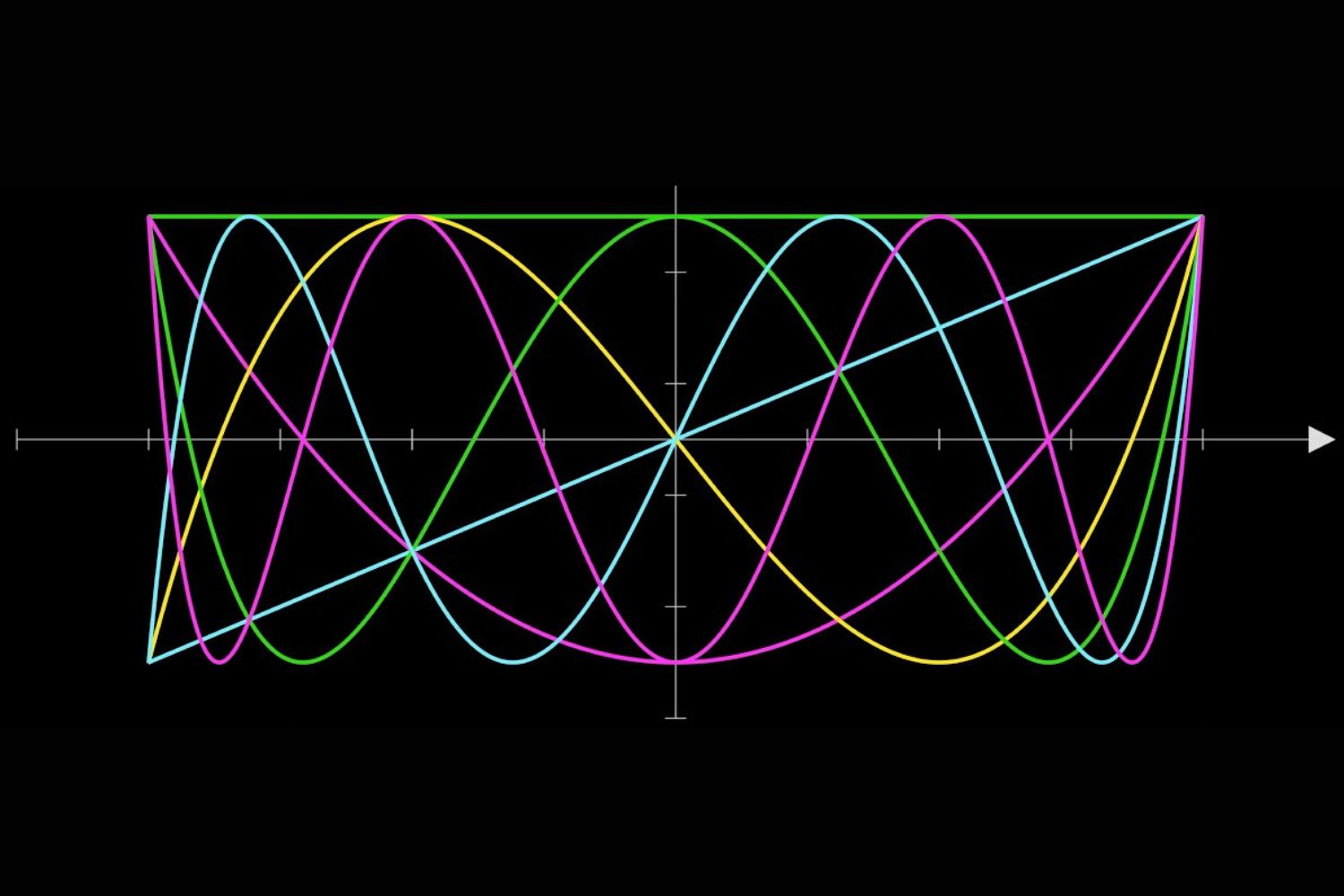
Chebyshev polynomials are a sequence of orthogonal polynomials that arise in various areas of mathematics, including approximation theory, numerical analysis, and algebra. Named after the Russian mathematician Pafnuty Chebyshev, these polynomials have unique properties that make them useful in solving complex problems.

1. Chebyshev polynomials are denoted as ( T_n(x) ) for the first kind and ( U_n(x) ) for the second kind.
2. The first few Chebyshev polynomials of the first kind are ( T_0(x) = 1 ), ( T_1(x) = x ), and ( T_2(x) = 2x^2 – 1 ).
3. Chebyshev polynomials of the second kind start with ( U_0(x) = 1 ), ( U_1(x) = 2x ), and ( U_2(x) = 4x^2 – 1 ).
4. These polynomials are orthogonal with respect to the weight function ( frac{1}{sqrt{1-x^2}} ) on the interval ([-1, 1]).
5. Chebyshev polynomials minimize the maximum error in polynomial approximation, making them ideal for numerical methods.

Historical Background

Understanding the history behind Chebyshev polynomials can provide context for their development and applications.

6. Pafnuty Chebyshev introduced these polynomials in the 19th century while studying the best approximation of functions.
7. Chebyshev's work laid the foundation for the field of approximation theory.
8. The polynomials were initially used to solve problems in mechanical engineering and physics.
9. Over time, their applications expanded to include computer science and signal processing.
10. Chebyshev's contributions to mathematics earned him recognition as one of the leading mathematicians of his time.

Mathematical Properties

Chebyshev polynomials possess several interesting mathematical properties that make them unique.

11. They satisfy the recurrence relation ( T_{n+1}(x) = 2xT_n(x) – T_{n-1}(x) ).
12. The roots of ( T_n(x) ) are given by ( x_k = cosleft(frac{(2k-1)pi}{2n}right) ) for ( k = 1, 2, ldots, n ).
13. Chebyshev polynomials can be expressed using trigonometric functions: ( T_n(x) = cos(n arccos(x)) ).
14. The leading coefficient of ( T_n(x) ) is ( 2^{n-1} ) for ( n geq 1 ).
15. They exhibit symmetry properties, such as ( T_n(-x) = (-1)^n T_n(x) ).

Applications in Numerical Analysis

Chebyshev polynomials are widely used in numerical analysis due to their advantageous properties.

16. They are used in polynomial interpolation to minimize Runge's phenomenon.
17. Chebyshev nodes, derived from the roots of Chebyshev polynomials, are used in numerical integration.
18. These polynomials are employed in spectral methods for solving differential equations.
19. Chebyshev polynomials help in designing efficient algorithms for fast Fourier transforms.
20. They are also used in the construction of orthogonal polynomial bases for function approximation.

Applications in Engineering and Physics

Beyond mathematics, Chebyshev polynomials find applications in various engineering and physics problems.

21. They are used in signal processing for filter design.
22. Chebyshev polynomials help in solving problems related to vibrations and wave propagation.
23. They are employed in control theory for system stability analysis.
24. These polynomials are used in the design of antennas and electromagnetic waveguides.
25. Chebyshev polynomials assist in solving problems in quantum mechanics and statistical mechanics.

Chebyshev Polynomials in Computer Science

In computer science, Chebyshev polynomials play a role in algorithms and data structures.

26. They are used in the design of efficient algorithms for polynomial evaluation.
27. Chebyshev polynomials help in the development of numerical methods for solving linear systems.
28. They are employed in the analysis of algorithms for numerical optimization.
29. These polynomials assist in the design of error-correcting codes.
30. Chebyshev polynomials are used in computer graphics for curve fitting and surface approximation.

Fun Facts and Trivia

Here are some fun and lesser-known facts about Chebyshev polynomials.

31. Chebyshev polynomials are named after Pafnuty Chebyshev, but they are also known as Tchebychev polynomials.
32. The Chebyshev polynomials of the first kind are related to the Chebyshev polynomials of the second kind by the relation ( U_n(x) = frac{T_{n+1}(x) – xT_n(x)}{1-x^2} ).
33. Chebyshev polynomials can be generalized to multiple variables, leading to multivariate Chebyshev polynomials.
34. They have applications in cryptography, particularly in the design of secure communication protocols.
35. Chebyshev polynomials are used in the analysis of random matrices and eigenvalue distributions.

Advanced Topics

For those interested in deeper mathematical exploration, Chebyshev polynomials offer advanced topics to study.

36. Generalized Chebyshev polynomials extend the concept to non-standard intervals and weight functions.
37. Chebyshev series provide a way to represent functions as infinite sums of Chebyshev polynomials.
38. The connection between Chebyshev polynomials and orthogonal polynomials in general is a rich area of research.
39. Chebyshev polynomials have applications in the theory of special functions and hypergeometric functions.
40. They are used in the study of dynamical systems and chaos theory.

Chebyshev Polynomials: A Quick Recap

Chebyshev polynomials are fascinating mathematical tools with wide-ranging applications. Named after Russian mathematician Pafnuty Chebyshev, these polynomials help solve complex problems in fields like numerical analysis, approximation theory, and even computer science. They minimize errors in polynomial approximations, making them invaluable for engineers and scientists.

Their unique properties, like orthogonality and the ability to form a basis for function spaces, set them apart. Chebyshev polynomials also play a crucial role in algorithms for fast Fourier transforms and solving differential equations.

Understanding these polynomials can open doors to advanced mathematical concepts and practical applications. Whether you're a student, a professional, or just a math enthusiast, knowing about Chebyshev polynomials enriches your mathematical toolkit. Dive into their world, and you'll find a treasure trove of knowledge waiting to be explored.