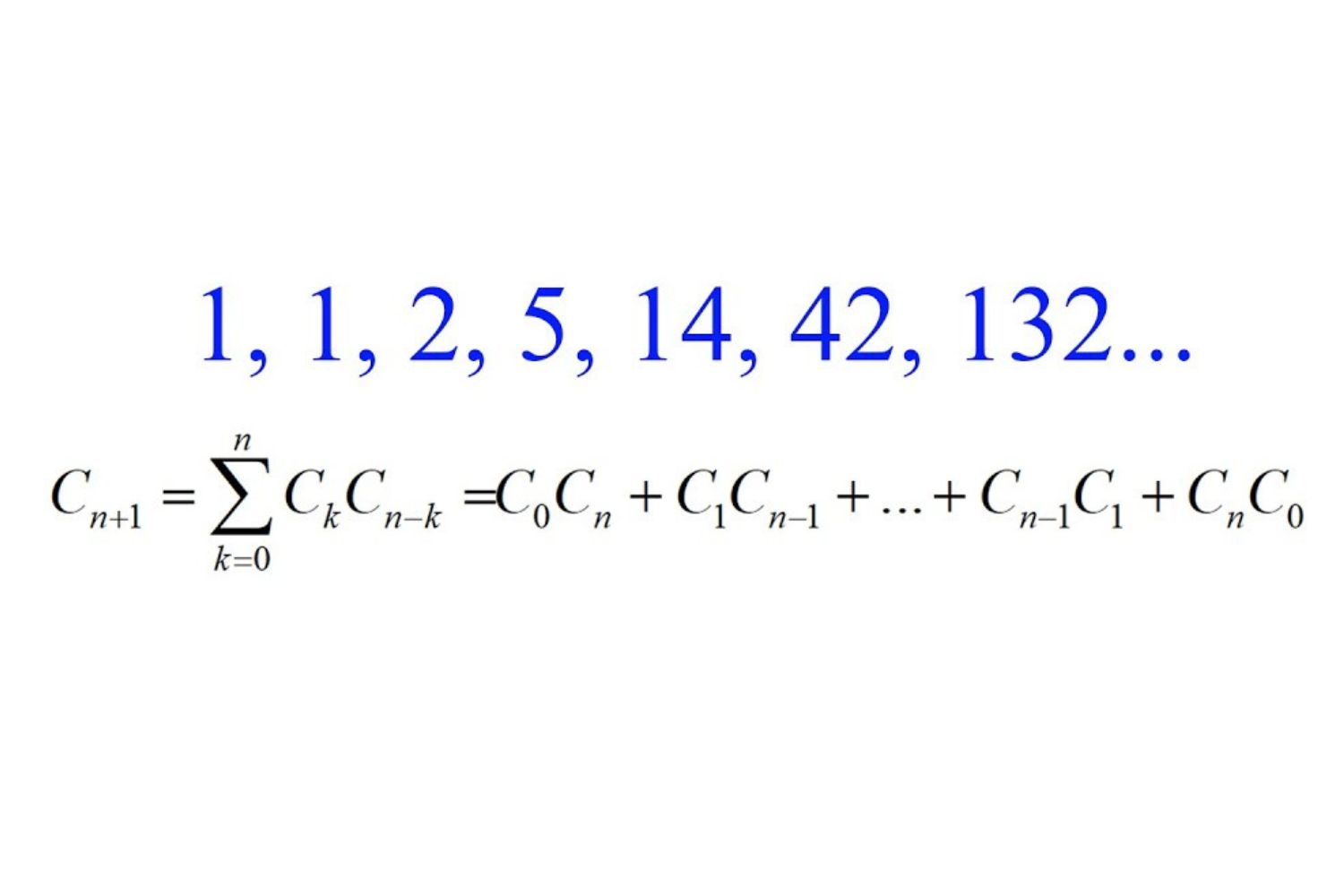
Catalan numbers might sound like something from a math wizard's spellbook, but they are actually a fascinating sequence of natural numbers with a wide range of applications. From counting the number of ways to correctly match parentheses in an expression to determining the number of distinct binary search trees with a given number of nodes, these numbers pop up in various mathematical problems. Named after the Belgian mathematician Eugène Charles Catalan, they have intrigued mathematicians for centuries. Whether you're a math enthusiast or just curious about the hidden patterns in numbers, learning about Catalan numbers can open up a whole new world of mathematical beauty. Ready to dive into 33 intriguing facts about Catalan numbers? Let's get started!
What are Catalan Numbers?
Catalan numbers are a sequence of natural numbers that have many applications in combinatorial mathematics. Named after the Belgian mathematician Eugène Charles Catalan, these numbers appear in various counting problems, often involving recursive structures. Let's dive into some fascinating facts about Catalan numbers.
Historical Background
Understanding the history behind Catalan numbers can provide context for their importance in mathematics.
- Eugène Charles Catalan first described these numbers in 1838.
- The sequence was independently discovered by other mathematicians, including Leonhard Euler.
- Catalan numbers were initially studied in the context of combinatorial problems.
Mathematical Definition
Catalan numbers have a specific formula that defines them. This formula helps in calculating the numbers in the sequence.
- The nth Catalan number is given by the formula: C(n) = (2n)! / ((n+1)!n!).
- The first few Catalan numbers are 1, 1, 2, 5, 14, 42, 132, and so on.
- They can also be defined recursively: C(0) = 1 and C(n+1) = Σ (C(i) * C(n-i)) for i=0 to n.
Applications in Combinatorics
Catalan numbers are incredibly useful in solving various combinatorial problems.
- They count the number of correct ways to match parentheses in an expression.
- They represent the number of rooted binary trees with n+1 leaves.
- They count the number of ways to triangulate a polygon with n+2 sides.
- They are used to determine the number of paths along the edges of a grid that do not pass above the diagonal.
Real-World Applications
Beyond theoretical mathematics, Catalan numbers have practical applications.
- They are used in computer science for parsing expressions and syntax trees.
- They help in the analysis of algorithms, particularly those involving recursive structures.
- They appear in the study of RNA secondary structures in biology.
Interesting Properties
Catalan numbers have several intriguing properties that make them a subject of interest.
- They are always integers, despite being defined by a fraction.
- They grow exponentially with n, but not as fast as factorials.
- They have a connection to the Fibonacci sequence through certain combinatorial interpretations.
Generalizations and Variations
There are several generalizations and variations of Catalan numbers that extend their utility.
- The Schröder numbers are a generalization that counts paths in a grid with certain restrictions.
- The Motzkin numbers are another variation that counts paths in a grid with different constraints.
- The Fuss-Catalan numbers generalize Catalan numbers to higher dimensions.
Catalan Numbers in Geometry
Catalan numbers also have geometric interpretations.
- They count the number of ways to dissect a convex polygon into smaller polygons using non-intersecting diagonals.
- They represent the number of ways to arrange non-intersecting chords between points on a circle.
- They are used in the study of polyhedra and their properties.
Catalan Numbers in Algebra
In algebra, Catalan numbers appear in various contexts.
- They are related to the coefficients in the expansion of certain polynomials.
- They appear in the study of free Lie algebras.
- They are used in the enumeration of certain types of lattice paths.
Catalan Numbers in Probability
Catalan numbers also have applications in probability theory.
- They are used in the study of random walks and their properties.
- They appear in the analysis of certain types of stochastic processes.
- They are used in the study of branching processes and their behavior.
Catalan Numbers in Computer Science
In computer science, Catalan numbers are used in various algorithms and data structures.
- They are used in the design of efficient algorithms for parsing expressions.
- They help in the analysis of recursive algorithms and their performance.
- They are used in the study of data structures such as binary search trees and heaps.
Catalan Numbers in Number Theory
Catalan numbers also have interesting properties in number theory.
- They are related to the binomial coefficients and their properties.
- They appear in the study of certain types of Diophantine equations.
The Magic of Catalan Numbers
Catalan numbers aren't just mathematical curiosities; they pop up in everyday life more than you'd think. From combinatorial problems to binary trees and even parentheses matching, these numbers have a knack for solving complex puzzles. They’re like the Swiss Army knife of math, versatile and handy in countless scenarios. Understanding them can give you a deeper appreciation for the hidden patterns in nature and technology.
Whether you’re a math enthusiast or just someone who loves quirky facts, Catalan numbers offer a fascinating glimpse into the world of numbers. They show how interconnected and beautiful mathematics can be. So next time you encounter a complex problem, remember, Catalan numbers might just hold the key. Dive into their world, and who knows what other secrets you might uncover?
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
