40 Facts About Reciprocal Lattice

What is a Reciprocal Lattice?

A reciprocal lattice is a concept used in physics and crystallography to describe the periodicity of a crystal in momentum space. It is the Fourier transform of the real-space lattice and plays a crucial role in understanding wave diffraction and electronic band structure.

1. The reciprocal lattice is constructed from the real-space lattice vectors.
2. It helps in analyzing diffraction patterns from X-ray, neutron, and electron diffraction experiments.
3. The points in a reciprocal lattice are called reciprocal lattice points.
4. Each point in the reciprocal lattice corresponds to a set of planes in the real-space lattice.
5. The reciprocal lattice of a simple cubic lattice is also a simple cubic lattice.

Importance in Crystallography

Reciprocal lattices are fundamental in crystallography, as they simplify the understanding of diffraction and the properties of crystals.

6. The concept was first introduced by physicist Paul Peter Ewald in 1913.
7. Reciprocal lattices are essential for interpreting Bragg's Law in diffraction studies.
8. They help in determining the crystal structure by analyzing the diffraction pattern.
9. The reciprocal lattice vector is perpendicular to the real-space lattice planes.
10. The magnitude of the reciprocal lattice vector is inversely proportional to the spacing between the planes in the real lattice.

Mathematical Representation

Understanding the mathematical representation of reciprocal lattices is key to utilizing them effectively in scientific research.

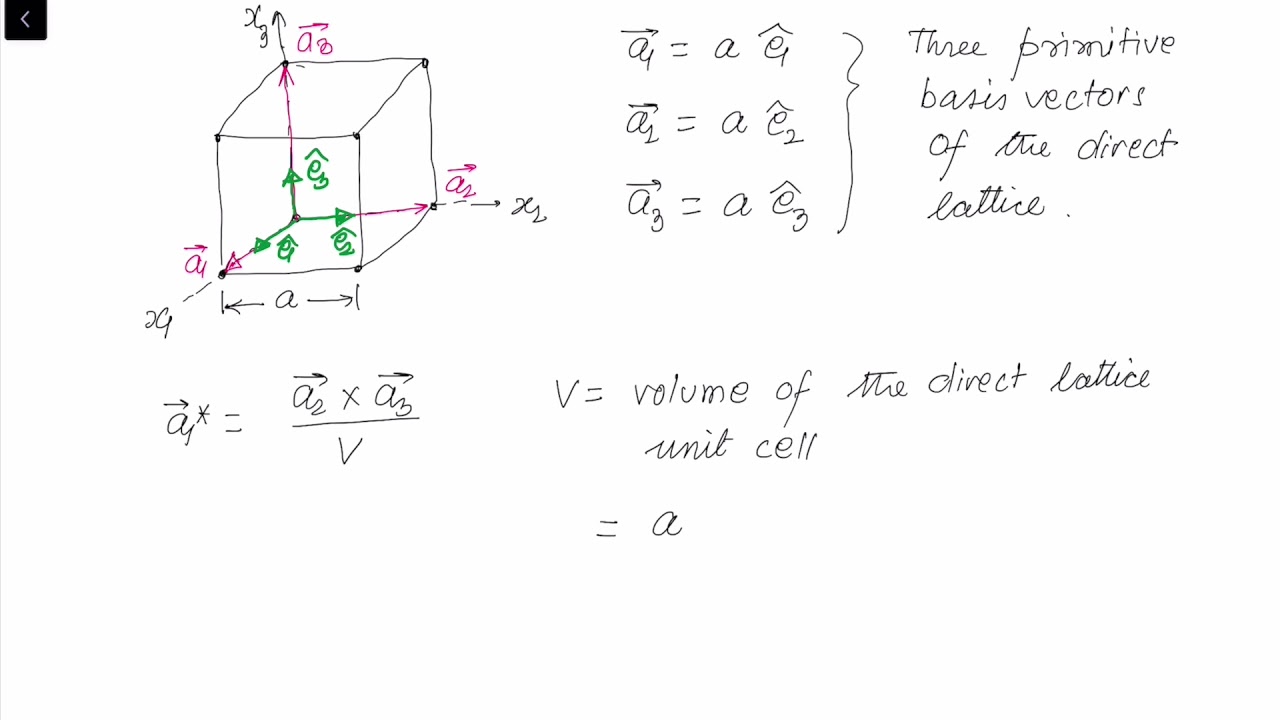
11. The reciprocal lattice vectors are defined as ( mathbf{b}_1 = 2pi frac{mathbf{a}_2 times mathbf{a}_3}{mathbf{a}_1 cdot (mathbf{a}_2 times mathbf{a}_3)} ), ( mathbf{b}_2 = 2pi frac{mathbf{a}_3 times mathbf{a}_1}{mathbf{a}_1 cdot (mathbf{a}_2 times mathbf{a}_3)} ), and ( mathbf{b}_3 = 2pi frac{mathbf{a}_1 times mathbf{a}_2}{mathbf{a}_1 cdot (mathbf{a}_2 times mathbf{a}_3)} ).
12. The reciprocal lattice of a body-centered cubic (BCC) lattice is a face-centered cubic (FCC) lattice.
13. Conversely, the reciprocal lattice of an FCC lattice is a BCC lattice.
14. The volume of the unit cell in reciprocal space is inversely proportional to the volume of the unit cell in real space.
15. Reciprocal lattice vectors are used to describe wave vectors in the crystal.

Applications in Physics

Reciprocal lattices are not just theoretical constructs; they have practical applications in various fields of physics.

16. They are used in the study of electronic band structures in solid-state physics.
17. Reciprocal lattices help in understanding the propagation of phonons in crystals.
18. They are crucial in the analysis of electron diffraction patterns.
19. The concept is used in the study of magnetic structures in materials.
20. Reciprocal lattices aid in the design of photonic crystals, which control the flow of light.

Visualization and Interpretation

Visualizing reciprocal lattices can be challenging but is essential for interpreting experimental data.

21. Reciprocal lattices can be represented graphically using software tools.
22. The Ewald sphere construction is a common method for visualizing diffraction conditions.
23. The Laue equations describe the conditions for diffraction in terms of reciprocal lattice vectors.
24. The reciprocal lattice can be used to predict the angles at which diffraction peaks will occur.
25. Visualization helps in understanding the symmetry properties of the crystal.

Advanced Topics

For those delving deeper into the subject, advanced topics in reciprocal lattices offer further insights.

26. The concept of the Brillouin zone, which is a uniquely defined primitive cell in reciprocal space.
27. The first Brillouin zone contains all the unique wave vectors that describe the periodicity of the crystal.
28. Higher-order Brillouin zones can be constructed by extending the boundaries of the first zone.
29. The concept of reciprocal space is extended to quasicrystals, which lack periodicity but have long-range order.
30. The study of reciprocal lattices is essential in the field of crystallography and materials science.

Practical Examples

Real-world examples help in understanding the practical significance of reciprocal lattices.

31. Silicon, a semiconductor, has a diamond cubic structure, and its reciprocal lattice is also a diamond cubic lattice.
32. Graphene, a single layer of carbon atoms, has a hexagonal lattice, and its reciprocal lattice is also hexagonal.
33. The analysis of X-ray diffraction patterns from proteins relies on the concept of reciprocal lattices.
34. The design of new materials, such as high-temperature superconductors, involves the study of their reciprocal lattices.
35. Reciprocal lattices are used in the development of new technologies, such as quantum computers.

Historical Context

Understanding the historical development of reciprocal lattices provides context to their importance.

36. The concept of reciprocal lattices was developed alongside the discovery of X-ray diffraction.
37. Early crystallographers used reciprocal lattices to solve complex crystal structures.
38. The development of electron microscopy techniques has relied on the principles of reciprocal lattices.
39. Advances in computational methods have made it easier to visualize and analyze reciprocal lattices.
40. The study of reciprocal lattices continues to be a dynamic and evolving field in science.

The Final Word on Reciprocal Lattice

Reciprocal lattices might sound complex, but they’re essential in understanding crystal structures. They help scientists analyze diffraction patterns, which reveal the arrangement of atoms in a crystal. This knowledge is crucial for developing new materials and improving existing ones. From X-ray diffraction to electron microscopy, reciprocal lattices play a key role in many scientific techniques.

Grasping the basics of reciprocal lattices can open doors to advanced studies in physics, chemistry, and materials science. They’re not just abstract concepts; they have real-world applications that impact technology and industry. Whether you’re a student, a researcher, or just curious, understanding reciprocal lattices can deepen your appreciation for the microscopic world.

So next time you hear about crystal structures or diffraction patterns, remember the reciprocal lattice. It’s a fundamental tool that helps unlock the secrets of the atomic world.