38 Facts About Saddle-Node Bifurcation

What is Saddle-Node Bifurcation?

Saddle-node bifurcation is a concept from mathematics, particularly in the study of dynamical systems. It describes a situation where two fixed points of a system, one stable and one unstable, collide and annihilate each other. This phenomenon has applications in various fields, including physics, biology, and engineering.

1. Saddle-node bifurcation occurs when a system's parameters change, causing two equilibrium points to merge and disappear.

2. Fixed points in a dynamical system are values where the system remains constant over time.

3. Stable fixed points attract nearby trajectories, meaning the system tends to return to these points after small disturbances.

4. Unstable fixed points repel nearby trajectories, causing the system to move away from these points after small disturbances.

Mathematical Representation

Understanding the mathematical representation of saddle-node bifurcation helps in visualizing and analyzing the phenomenon.

5. The normal form of a saddle-node bifurcation can be written as ( dot{x} = r + x^2 ), where ( r ) is a parameter.

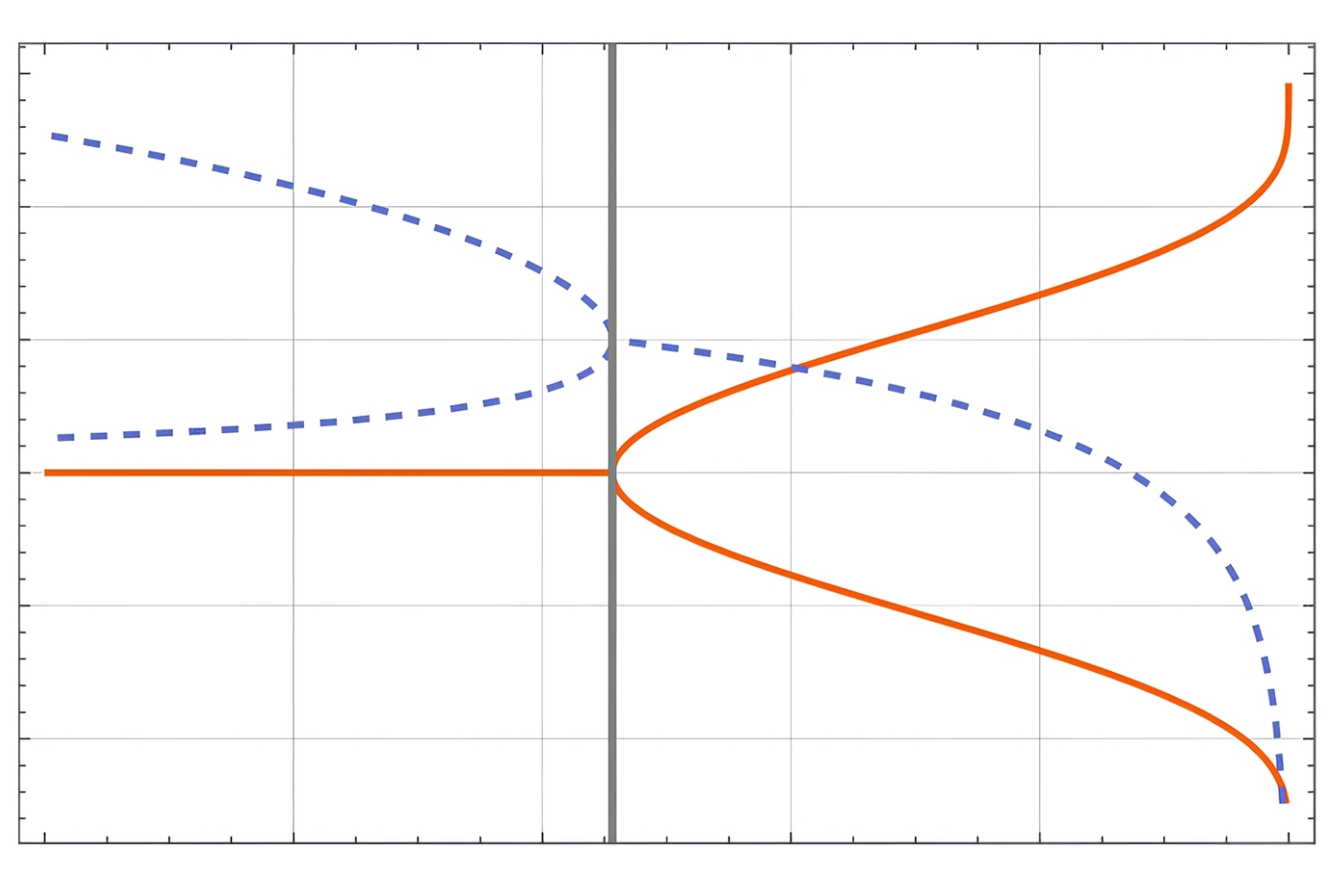
6. Bifurcation diagrams plot the fixed points of a system against a parameter, showing how the points change as the parameter varies.

7. In a bifurcation diagram, a saddle-node bifurcation appears as a point where two branches of fixed points meet and disappear.

8. Eigenvalues of the Jacobian matrix at the fixed points determine their stability.

Real-World Applications

Saddle-node bifurcation isn't just a theoretical concept; it has practical applications in various fields.

9. In ecology, saddle-node bifurcation can model population dynamics, such as predator-prey interactions.

10. Electrical circuits can exhibit saddle-node bifurcation, affecting the stability of the circuit's operation.

11. Mechanical systems like bridges and buildings can experience saddle-node bifurcation, leading to structural failures.

12. Climate models use saddle-node bifurcation to study tipping points in climate systems.

Biological Systems

Biological systems often display complex behaviors that can be analyzed using saddle-node bifurcation.

13. Neural activity in the brain can be modeled using saddle-node bifurcation to understand how neurons switch between active and inactive states.

14. Gene regulation networks can exhibit saddle-node bifurcation, affecting how genes are expressed in cells.

15. Cardiac rhythms can be analyzed using saddle-node bifurcation to understand irregular heartbeats.

Historical Context

The concept of saddle-node bifurcation has a rich history in the study of dynamical systems.

16. Henri Poincaré, a French mathematician, made significant contributions to the study of dynamical systems, including saddle-node bifurcation.

17. Andronov and Pontryagin further developed the theory of bifurcations in the 1930s.

18. The term "saddle-node bifurcation" was popularized in the 20th century as the study of dynamical systems grew.

Visualizing Saddle-Node Bifurcation

Visual tools help in understanding and teaching the concept of saddle-node bifurcation.

19. Phase portraits are graphical representations of the trajectories of a dynamical system in its phase space.

20. In a phase portrait, a saddle-node bifurcation appears as a point where trajectories converge or diverge.

21. Simulation software like MATLAB and Mathematica can be used to create bifurcation diagrams and phase portraits.

Challenges and Limitations

Despite its usefulness, saddle-node bifurcation has limitations and challenges.

22. Nonlinear systems can be difficult to analyze, requiring advanced mathematical techniques.

23. Parameter estimation in real-world systems can be challenging, affecting the accuracy of bifurcation analysis.

24. Noise and disturbances in real-world systems can complicate the identification of saddle-node bifurcation.

Advanced Topics

For those interested in delving deeper, there are advanced topics related to saddle-node bifurcation.

25. Codimension-two bifurcations involve two parameters and can lead to more complex behaviors.

26. Global bifurcations occur when changes in the system's parameters affect the entire phase space.

27. Homoclinic bifurcations involve trajectories that converge to a saddle point both forward and backward in time.

Practical Examples

Examples help in understanding how saddle-node bifurcation manifests in real systems.

28. Laser dynamics can exhibit saddle-node bifurcation, affecting the stability of laser output.

29. Chemical reactions can show saddle-node bifurcation, influencing reaction rates and equilibrium states.

30. Economic models can use saddle-node bifurcation to study market stability and crashes.

Research and Development

Ongoing research continues to explore new aspects and applications of saddle-node bifurcation.

31. Quantum systems are being studied to understand how saddle-node bifurcation affects quantum states.

32. Robotics uses saddle-node bifurcation to design stable control systems for robots.

33. Artificial intelligence can benefit from saddle-node bifurcation analysis to improve learning algorithms.

Educational Resources

Learning about saddle-node bifurcation can be facilitated through various educational resources.

34. Textbooks on dynamical systems often include chapters on bifurcations, including saddle-node bifurcation.

35. Online courses and tutorials provide interactive learning experiences on saddle-node bifurcation.

36. Research papers offer in-depth analyses and case studies on saddle-node bifurcation.

Future Directions

The study of saddle-node bifurcation continues to evolve, with new discoveries and applications on the horizon.

37. Interdisciplinary research is exploring how saddle-node bifurcation can be applied across different fields.

38. Technological advancements are enabling more precise and detailed studies of saddle-node bifurcation in complex systems.

The Final Word on Saddle-Node Bifurcation

Saddle-node bifurcation might sound complex, but it’s a fundamental concept in understanding dynamic systems. This phenomenon occurs when two fixed points, one stable and one unstable, collide and annihilate each other. It’s crucial in fields like physics, biology, and engineering, helping predict system behaviors and potential failures.

Grasping this concept can illuminate how systems transition from stable to chaotic states. Whether you’re a student, researcher, or just curious, knowing about saddle-node bifurcation enriches your understanding of the world’s intricate patterns.

So, next time you encounter a sudden change in a system, think about saddle-node bifurcation. It’s a small piece of the puzzle that explains much about how things work. Keep exploring, stay curious, and remember, even the most complex ideas can be broken down into understandable facts.