The Klein-Nishina Formula is a fundamental concept in physics that has revolutionized our understanding of photon-electron interactions. Developed by Oskar Klein and Yoshio Nishina in the 1920s, this formula provides a mathematical description of the scattering of photons by electrons. It has been instrumental in various fields of physics, including quantum mechanics, particle physics, and astrophysics.
In this article, we will delve into the intricacies of the Klein-Nishina Formula and uncover 18 fascinating facts that highlight its significance in the world of physics. From its derivation to its applications in understanding the behavior of light and matter, we will explore how this formula has shaped our understanding of the fundamental interactions of particles.
Key Takeaways:
- The Klein-Nishina formula helps scientists understand how light interacts with electrons, impacting fields like astrophysics and radiation therapy. It’s like a secret code revealing the behavior of particles in the quantum world!
- By describing the scattering of photons by electrons, the Klein-Nishina formula has paved the way for advancements in particle physics and high-energy particle accelerators. It’s like a superhero guiding scientists to unlock the mysteries of the universe!
Origin
The Klein-Nishina formula, named after physicists Oskar Klein and Yoshio Nishina, was developed in the early 20th century as a way to describe the scattering of photons by free electrons. It played a crucial role in the advancement of quantum electrodynamics.
Quantum Electrodynamics
The Klein-Nishina formula is an essential component of quantum electrodynamics, a branch of physics that deals with the interaction between light and matter. It provides a mathematical framework for understanding how photons interact with electrons in various scattering processes.
Scattering of Photons
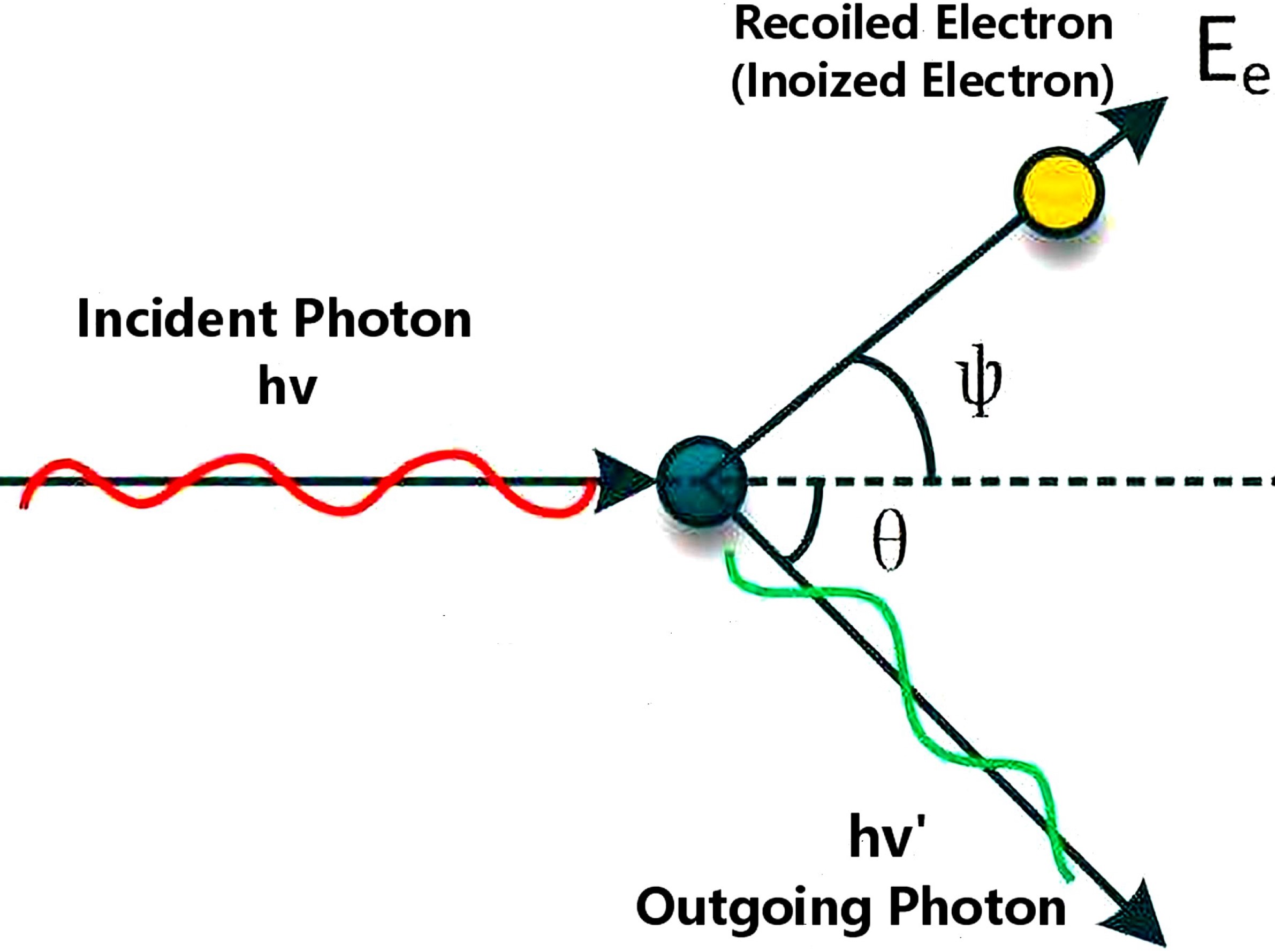
The formula specifically describes the differential cross-section of photons scattered by free electrons. It allows scientists to calculate the probability of a photon being scattered at a particular angle and energy after interacting with an electron.
Compton Scattering
One of the most significant applications of the Klein-Nishina formula is in the field of Compton scattering. This phenomenon involves the scattering of X-ray and gamma-ray photons by electrons, resulting in a shift in the wavelength of the scattered radiation.
Relativistic Electrons
The Klein-Nishina formula takes into account the relativistic nature of electrons, which is crucial when studying high-energy photon interactions. It helps physicists understand the behavior of electrons moving at speeds close to the speed of light.
Photon Polarization
The formula also allows for the consideration of photon polarization. By taking into account the polarization state of the incident photon, scientists can better understand the scattering processes and the interaction between the photon and the electron.
Energy Dependence
The Klein-Nishina formula demonstrates the energy dependence of photon-electron scattering. It shows that the probability of scattering is highly dependent on the energy of the incident photon, with higher energies resulting in different scattering patterns.
Quantum Nature of Light
The Klein-Nishina formula serves as a reminder of the quantum nature of light. By describing the scattering of photons by electrons, it emphasizes that light consists of discrete particles known as photons, which behave both as particles and waves.
Applications in Astrophysics
The Klein-Nishina formula finds extensive use in astrophysics, particularly in the study of high-energy phenomena such as gamma-ray bursts and active galactic nuclei. It helps scientists understand the interactions between photons and electrons in extreme cosmic environments.
Quantum Field Theory
The formula’s incorporation into quantum electrodynamics contributes to the development of quantum field theory. It provides a mathematical framework for understanding the fundamental processes involving particles and fields.
Experimental Verification
Experiments have been conducted to verify the predictions of the Klein-Nishina formula. By measuring the scattered photons’ energy and angle distribution, scientists can compare the results with the theoretical predictions to validate the formula’s accuracy.
Multiple Particle Systems
The Klein-Nishina formula can be extended to describe scattering processes involving multiple particles, such as electrons and positrons. This expansion allows for a deeper understanding of interactions within complex systems.
Quantum Mechanics and Special Relativity
The formula embodies the synergy between quantum mechanics and special relativity. It combines the principles of both fields to accurately describe the scattering processes involving high-energy photons and relativistic electrons.
Cross-Section Dependence
The Klein-Nishina formula demonstrates the cross-section dependence on various factors, such as the scattering angle, photon energy, and electron mass. This dependence provides valuable insights into the probability and intensity of scattering events.
Importance in Radiation Therapy
In the field of radiation therapy, the Klein-Nishina formula plays a critical role in understanding the interaction between high-energy photons and biological tissues. This knowledge aids in the precise targeting of cancer cells while minimizing damage to healthy cells.
Development of High-Energy Particle Accelerators
The understanding of photon-electron interactions based on the Klein-Nishina formula has contributed to the advancements in high-energy particle accelerators. This knowledge helps scientists design and optimize accelerators for a wide range of applications.
Contributions to Particle Physics
The Klein-Nishina formula’s insights into scattering processes have made significant contributions to the field of particle physics. It aids in the study of fundamental particles, their properties, and their interactions in particle accelerators around the world.
Impact on Modern Physics
The Klein-Nishina formula’s impact extends beyond its direct applications. Its development and incorporation into quantum electrodynamics have paved the way for other breakthroughs in modern physics, contributing to our understanding of the fundamental nature of the universe.
Conclusion
The Klein-Nishina formula is a crucial concept in the field of physics that helps us understand how photons interact with electrons. By considering the quantum nature of particles and the principles of scattering, this formula provides valuable insights into phenomena such as Compton scattering. Through its mathematical framework, it allows us to analyze the probability and distribution of scattered photons, ultimately contributing to our understanding of the behavior of particles and the fundamental principles of quantum mechanics.
FAQs
1. What is the Klein-Nishina formula?
The Klein-Nishina formula is an equation in physics that describes the scattering of photons by free electrons. It takes into account the quantum nature of particles and provides a mathematical framework for analyzing the probability and distribution of scattered photons.
2. Who developed the Klein-Nishina formula?
The Klein-Nishina formula was developed independently by the physicists Oskar Klein and Yoshio Nishina in 1929. It built upon the earlier work of Arthur Compton and helped to further our understanding of the scattering of X-rays and gamma rays by matter.
3. What is the significance of the Klein-Nishina formula?
The Klein-Nishina formula is significant because it allows us to quantitatively analyze the scattering of photons by electrons, taking into account their quantum properties. This formula is crucial in various fields of physics, including nuclear physics, particle physics, and astrophysics.
4. How does the Klein-Nishina formula contribute to our understanding of quantum mechanics?
By considering the behavior of particles at the microscopic level, the Klein-Nishina formula contributes to our understanding of quantum mechanics. It helps us comprehend how particles interact with each other and how their properties, such as energy and momentum, are affected during scattering processes.
5. Are there any practical applications of the Klein-Nishina formula?
Yes, the Klein-Nishina formula has practical applications in various fields. It is used in medical imaging techniques such as X-ray imaging and computed tomography (CT) scans. It also plays a crucial role in understanding the behavior of high-energy particles in particle accelerators and contributes to research in nuclear physics and astrophysics.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
