38 Facts About Isometry

What is Isometry?

Isometry might sound like a complex term, but it's simpler than you think. It refers to a transformation in geometry that preserves distances between points. Let's dive into some fascinating facts about isometry.

1. 01

   Isometry comes from Greek words: The term "isometry" combines "iso," meaning equal, and "metron," meaning measure. It literally means "equal measure."

2. 02

   Preserves distances: In an isometric transformation, the distance between any two points remains unchanged. This means if two points are 5 units apart before the transformation, they will still be 5 units apart afterward.

3. 03

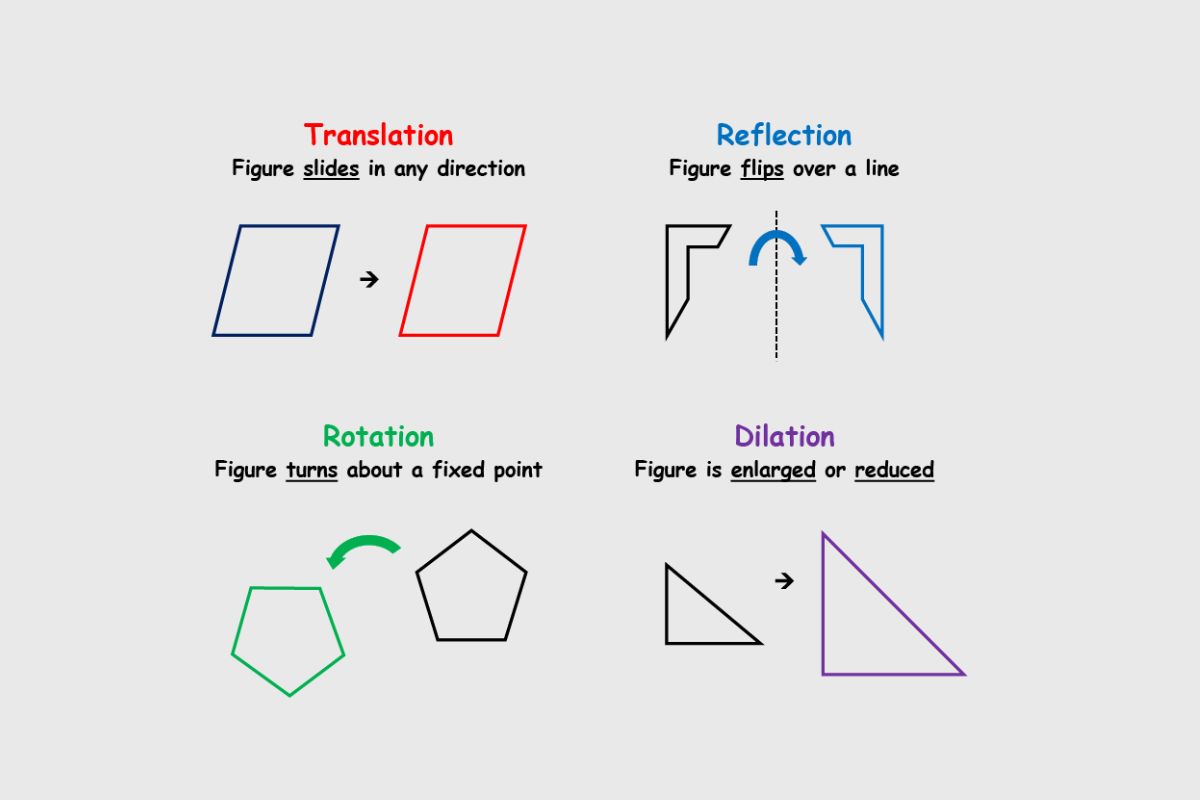
   Types of isometries: There are four main types: translations, rotations, reflections, and glide reflections. Each type moves or changes a shape without altering its size or proportions.

4. 04

   Used in computer graphics: Isometry is crucial in computer graphics and animations. It helps create realistic movements and transformations of objects without distorting their shapes.

5. 05

   Common in nature: Many natural processes and structures exhibit isometric properties. For example, the way certain crystals grow or how some animals move.

Types of Isometries

Understanding the different types of isometries can help you see how they apply in various fields, from art to engineering.

6. 06

   Translation: This type moves every point of a shape the same distance in the same direction. Imagine sliding a book across a table without rotating it.

7. 07

   Rotation: Involves turning a shape around a fixed point. Think of spinning a wheel around its axle.

8. 08

   Reflection: Flips a shape over a line, creating a mirror image. It's like seeing your reflection in a pond.

9. 09

   Glide reflection: Combines a reflection and a translation. Picture walking forward while looking at your reflection in a mirror.

10. 10

    Identity transformation: This is a special case where the shape remains exactly the same. No movement or change occurs.

Applications of Isometry

Isometry isn't just a theoretical concept; it has practical applications in various fields.

11. 11

    Architecture: Architects use isometry to design buildings and structures that are both functional and aesthetically pleasing.

12. 12

    Robotics: Robots often rely on isometric transformations to navigate and manipulate objects accurately.

13. 13

    Medical imaging: Techniques like MRI and CT scans use isometry to create accurate images of the human body.

14. 14

    Video games: Game developers use isometry to create realistic environments and character movements.

15. 15

    Art: Artists use isometric techniques to create perspective and depth in their work.

Mathematical Properties of Isometry

Isometry has several interesting mathematical properties that make it a fundamental concept in geometry.

16. 16

    Distance preservation: As mentioned earlier, isometry keeps the distance between points unchanged.

17. 17

    Angle preservation: Isometric transformations also preserve angles between lines. This means the shape's internal angles remain the same.

18. 18

    Area preservation: The area of a shape remains constant under an isometric transformation. A triangle with an area of 10 square units will still have the same area after being rotated or reflected.

19. 19

    Orientation: Some isometries, like rotations and translations, preserve the orientation of a shape, while others, like reflections, do not.

20. 20

    Compositions: Combining two or more isometries results in another isometry. For example, a rotation followed by a translation is still an isometric transformation.

Isometry in Different Dimensions

Isometry isn't limited to two-dimensional shapes; it also applies to three-dimensional objects and beyond.

21. 21

    2D isometries: These include translations, rotations, reflections, and glide reflections, as discussed earlier.

22. 22

    3D isometries: In three dimensions, isometries include translations, rotations, reflections, and glide reflections, but they also involve more complex movements like screw rotations.

23. 23

    Higher dimensions: Isometries can be extended to higher dimensions, although visualizing them becomes more challenging. Mathematicians study these to understand complex geometric structures.

24. 24

    Rigid motions: In any dimension, isometries are often referred to as rigid motions because they don't deform the shape.

Historical Context of Isometry

Isometry has a rich history, with contributions from many mathematicians over the centuries.

25. 25

    Euclid's Elements: The ancient Greek mathematician Euclid laid the groundwork for the study of isometry in his famous work, "Elements."

26. 26

    Felix Klein: In the 19th century, German mathematician Felix Klein developed the Erlangen Program, which classified geometries based on their isometries.

27. 27

    Sophus Lie: Norwegian mathematician Sophus Lie made significant contributions to the study of continuous isometries and their applications.

28. 28

    Modern developments: Today, isometry continues to be a vital area of research in mathematics, with applications in fields like topology and differential geometry.

Fun Facts about Isometry

Let's wrap up with some fun and quirky facts about isometry that you might not know.

29. 29

    Origami: The art of paper folding relies heavily on isometric transformations to create intricate designs.

30. 30

    Escher's art: M.C. Escher, a famous Dutch artist, used isometric transformations to create mind-bending artworks.

31. 31

    Tessellations: Isometry plays a key role in creating tessellations, which are patterns of shapes that fit together without gaps or overlaps.

32. 32

    Rubik's Cube: Solving a Rubik's Cube involves understanding isometric transformations to manipulate the puzzle.

33. 33

    Symmetry: Many symmetrical patterns in nature, like snowflakes and honeycombs, are examples of isometric transformations.

34. 34

    Dance: Some dance moves, especially in ballet and gymnastics, can be described using isometric transformations.

35. 35

    Sports: Athletes often use isometric exercises to build strength without changing the length of their muscles.

36. 36

    Puzzles: Many brain-teasing puzzles, like tangrams and jigsaw puzzles, involve isometric transformations.

37. 37

    Virtual reality: VR technology uses isometry to create immersive, realistic experiences for users.

38. 38

    Astronomy: Astronomers use isometric transformations to study the shapes and movements of celestial bodies.

The Final Word on Isometry

Isometry isn't just a fancy term. It’s a key concept in geometry and mathematics that helps us understand shapes, spaces, and transformations. From preserving distances to maintaining angles, isometry plays a crucial role in fields like computer graphics, robotics, and even architecture. Whether you're a student, a professional, or just a curious mind, knowing about isometry can give you a new perspective on how the world works. It’s fascinating to see how something so abstract can have such practical applications. So next time you see a reflection, rotation, or translation, remember that isometry is at play. Keep exploring, keep questioning, and who knows? You might just find yourself seeing the world in a whole new way.