37 Facts About Group Cohomology

What is Group Cohomology?

Group cohomology is a mathematical concept that studies the properties of groups using cohomological techniques. It provides insights into the structure and classification of groups, especially in algebra and topology.

1. 01Group cohomology originated from the work of Henri Cartan and Samuel Eilenberg in the 1940s.
2. 02It is a tool used to study extensions of groups and modules.
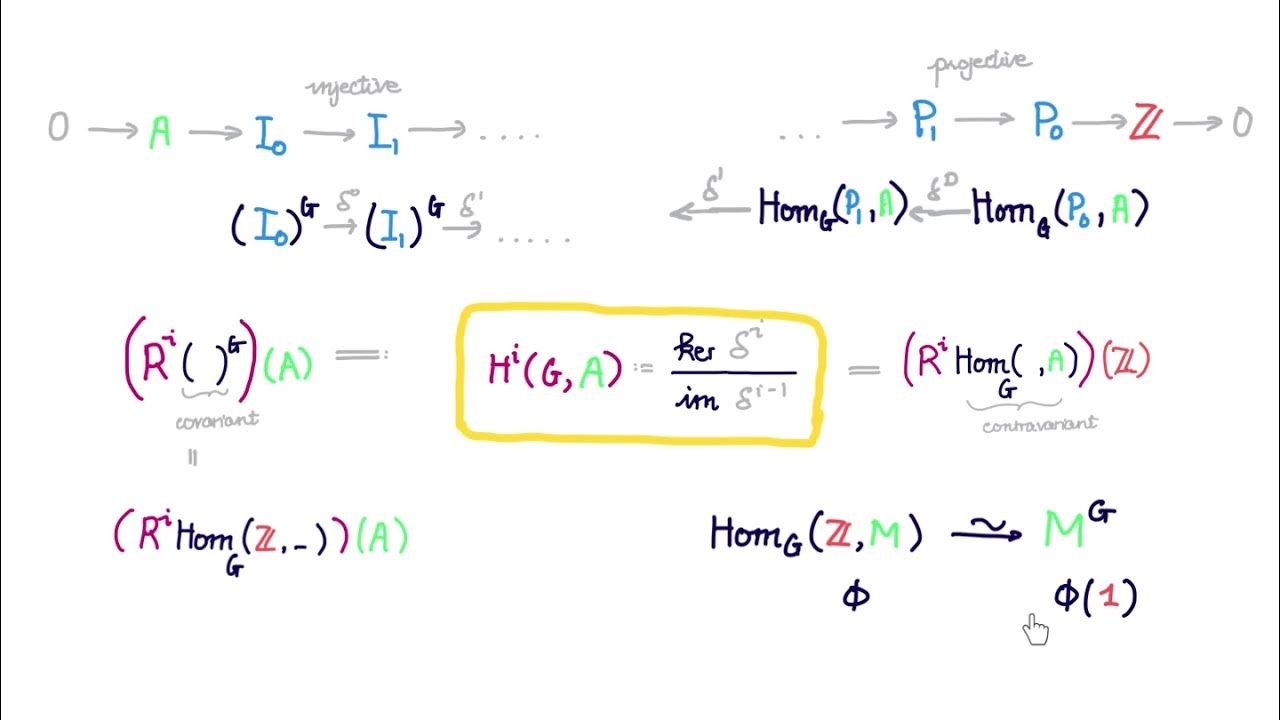
3. 03The first cohomology group, denoted ( H^1(G, M) ), classifies the extensions of a group ( G ) by a module ( M ).
4. 04Group cohomology can be used to study the actions of groups on various algebraic structures.
5. 05It has applications in number theory, particularly in the study of Galois cohomology.

Basic Concepts in Group Cohomology

Understanding the basic concepts is crucial for diving deeper into group cohomology. These concepts lay the foundation for more advanced topics.

6. 06A cochain is a function that assigns values to group elements in a consistent way.
7. 07The coboundary operator is a function that maps cochains to cochains, helping to define cohomology groups.
8. 08A cocycle is a cochain that satisfies a specific condition related to the coboundary operator.
9. 09A coboundary is a cochain that can be expressed as the coboundary of another cochain.
10. 10The nth cohomology group, ( H^n(G, M) ), is defined as the quotient of the group of n-cocycles by the group of n-coboundaries.

Applications of Group Cohomology

Group cohomology has a wide range of applications in various fields of mathematics and science. These applications demonstrate its versatility and importance.

11. 11In algebraic topology, group cohomology is used to study the properties of topological spaces.
12. 12It helps in the classification of fiber bundles.
13. 13Group cohomology is used in the study of algebraic groups and their representations.
14. 14It plays a role in the theory of Lie groups and Lie algebras.
15. 15In number theory, it is used to study the arithmetic properties of fields.

Advanced Topics in Group Cohomology

For those who want to delve deeper, advanced topics in group cohomology offer a more comprehensive understanding of the subject.

16. 16Spectral sequences are a tool used to compute cohomology groups in complex situations.
17. 17The Lyndon-Hochschild-Serre spectral sequence is a specific type of spectral sequence used in group cohomology.
18. 18Group cohomology can be generalized to the cohomology of topological groups.
19. 19The cohomology of profinite groups is an important area of study in number theory.
20. 20Continuous cohomology is a variant of group cohomology used for topological groups.

Historical Development of Group Cohomology

The history of group cohomology is rich and filled with contributions from many prominent mathematicians. Understanding its development provides context for its current state.

21. 21Henri Cartan and Samuel Eilenberg laid the foundations of group cohomology in the 1940s.
22. 22The concept was further developed by John Tate in the 1950s.
23. 23Michael Atiyah and Isadore Singer used group cohomology in their famous index theorem.
24. 24Jean-Pierre Serre made significant contributions to the field in the 1960s.
25. 25The development of spectral sequences revolutionized the computation of cohomology groups.

Key Theorems in Group Cohomology

Several key theorems form the backbone of group cohomology. These theorems provide essential tools and results used in the study of cohomology.

26. 26The Universal Coefficient Theorem relates the cohomology of a group to its homology.
27. 27Shapiro's Lemma provides a way to compute cohomology groups using induced modules.
28. 28The Eckmann-Shapiro Lemma is a generalization of Shapiro's Lemma.
29. 29The Five Lemma is a tool used in homological algebra to compare cohomology groups.
30. 30The Snake Lemma is used to derive long exact sequences in cohomology.

Computational Techniques in Group Cohomology

Computing cohomology groups can be challenging, but several techniques and tools have been developed to simplify the process.

31. 31The use of spectral sequences allows for the step-by-step computation of cohomology groups.
32. 32Computer algebra systems, such as GAP and SageMath, can be used to compute cohomology groups.
33. 33The cohomology ring of a group provides a way to organize and compute cohomology groups.
34. 34The use of simplicial complexes can simplify the computation of cohomology groups.
35. 35Homological algebra techniques, such as projective resolutions, are used to compute cohomology groups.

Future Directions in Group Cohomology

Group cohomology continues to evolve, with new research and applications emerging regularly. These future directions highlight the ongoing importance of the field.

36. 36The study of higher-dimensional cohomology groups is an active area of research.
37. 37Applications of group cohomology in quantum computing and cryptography are being explored.

The Final Word on Group Cohomology

Group cohomology, though complex, plays a crucial role in modern mathematics. It bridges algebra and topology, providing insights into group actions, extensions, and more. Understanding its basics can open doors to advanced studies in various fields. Remember, cohomology isn't just abstract theory; it has practical applications in coding theory, cryptography, and even physics. Whether you're a math enthusiast or a professional, grasping these concepts can be incredibly rewarding. Keep exploring, stay curious, and don't shy away from the challenging parts. With patience and practice, the intricate world of group cohomology will start to make sense, revealing its beauty and utility. So, dive in, and let your mathematical journey continue!