34 Facts About Partial Differential Equations

What are Partial Differential Equations?

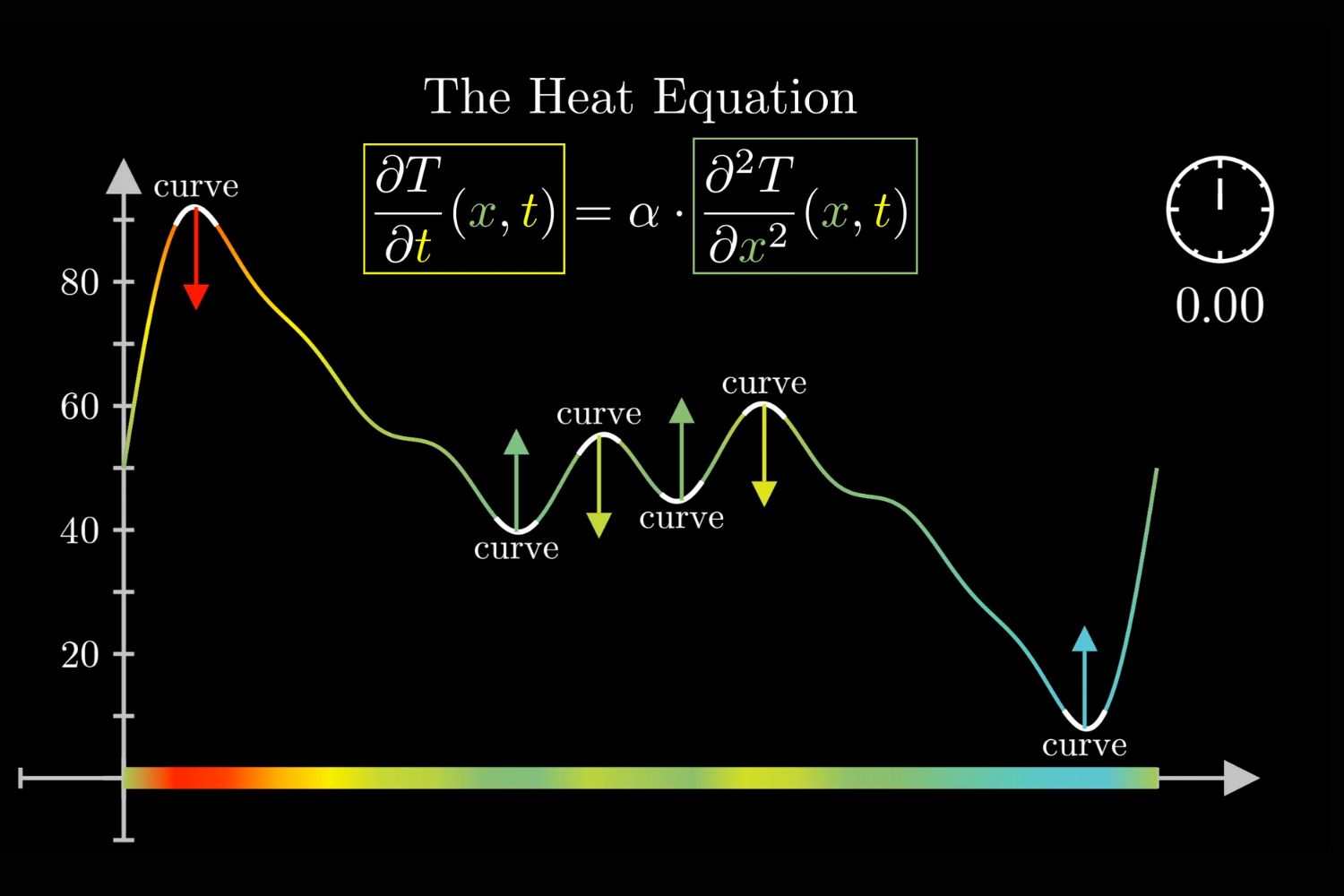
Partial Differential Equations (PDEs) are equations involving functions and their partial derivatives. They play a crucial role in various scientific fields, from physics to engineering.

1. PDEs describe how physical quantities change over space and time.
2. They are essential in modeling phenomena like heat conduction, wave propagation, and fluid dynamics.
3. The term "partial" refers to the fact that these equations involve partial derivatives, which are derivatives with respect to one variable while keeping others constant.
4. PDEs can be linear or nonlinear, with linear PDEs being easier to solve.
5. The study of PDEs dates back to the 18th century, with significant contributions from mathematicians like Euler and Lagrange.

Types of Partial Differential Equations

PDEs come in various forms, each suited for different types of problems. Understanding these types helps in selecting the right method for solving them.

6. Elliptic PDEs: These equations describe steady-state phenomena, like the distribution of temperature in a solid object.
7. Parabolic PDEs: Used for time-dependent processes, such as heat diffusion.
8. Hyperbolic PDEs: These equations model wave propagation, like sound waves or seismic waves.
9. Mixed-type PDEs: Some equations can change type depending on the region of the solution space.
10. Quasilinear PDEs: These involve linear terms but can have nonlinear coefficients.

Applications of Partial Differential Equations

PDEs are not just theoretical constructs; they have practical applications in various fields.

11. Physics: PDEs describe fundamental laws like Maxwell's equations for electromagnetism.
12. Engineering: Used in structural analysis, fluid mechanics, and aerodynamics.
13. Biology: Model population dynamics and the spread of diseases.
14. Economics: PDEs help in modeling financial markets and option pricing.
15. Meteorology: Weather prediction models rely heavily on PDEs.

Methods for Solving Partial Differential Equations

Solving PDEs can be challenging, but several methods have been developed to tackle this problem.

16. Separation of Variables: This technique simplifies a PDE into simpler, solvable ODEs.
17. Fourier Transform: Converts a PDE into an algebraic equation, making it easier to solve.
18. Finite Difference Method: Approximates derivatives using difference equations.
19. Finite Element Method: Breaks down a complex problem into smaller, simpler parts.
20. Spectral Methods: Use orthogonal polynomials to approximate solutions.

Famous Partial Differential Equations

Some PDEs have become famous due to their wide-ranging applications and the challenges they present.

21. Laplace's Equation: Describes steady-state heat distribution and electrostatics.
22. Heat Equation: Models the distribution of heat in a given region over time.
23. Wave Equation: Describes the propagation of waves, like sound or light waves.
24. Navier-Stokes Equations: Govern the motion of fluid substances.
25. Schrödinger Equation: Fundamental in quantum mechanics, describing how quantum states evolve.

Challenges in Solving Partial Differential Equations

Despite their importance, solving PDEs is not always straightforward.

26. Nonlinearity: Nonlinear PDEs are particularly challenging to solve.
27. Boundary Conditions: Solutions often depend heavily on the conditions at the boundaries of the domain.
28. Initial Conditions: For time-dependent PDEs, initial conditions can significantly affect the solution.
29. Computational Complexity: Numerical methods can be computationally intensive.
30. Existence and Uniqueness: Proving that a solution exists and is unique can be difficult.

Modern Developments in Partial Differential Equations

The field of PDEs continues to evolve, with new methods and applications emerging regularly.

31. Machine Learning: AI techniques are being used to approximate solutions to complex PDEs.
32. High-Performance Computing: Advances in computing power allow for the simulation of more complex systems.
33. Multiscale Modeling: Combines PDEs at different scales to model complex phenomena.
34. Fractional PDEs: These involve derivatives of non-integer order and have applications in various fields, including finance and biology.

The Final Word on Partial Differential Equations

Partial Differential Equations (PDEs) are the backbone of many scientific and engineering fields. They help us understand complex phenomena like heat transfer, wave propagation, and fluid dynamics. By solving PDEs, we can predict weather patterns, design better materials, and even simulate the behavior of financial markets.

Understanding the basics of PDEs opens up a world of possibilities. Whether you're a student, a researcher, or just curious, grasping these equations can be incredibly rewarding. They might seem daunting at first, but with practice, their patterns and solutions become clearer.

Remember, PDEs aren't just abstract math; they're tools that shape our world. So next time you see a weather forecast or marvel at a new technology, think about the partial differential equations working behind the scenes. Keep exploring, keep questioning, and let the power of PDEs inspire you.