What are circular functions? Circular functions, also known as trigonometric functions, are mathematical functions that relate angles of a triangle to the lengths of its sides. These functions include sine, cosine, and tangent, among others. Why are they important? They play a crucial role in various fields such as physics, engineering, and computer science. How do they work? Circular functions use the unit circle, a circle with a radius of one, to define the values of these functions for different angles. What are some interesting facts? From their historical origins in ancient civilizations to their modern applications in technology, circular functions have a rich and fascinating history. Why should you care? Understanding these functions can help you solve real-world problems, from calculating distances to designing electronic circuits.
What Are Circular Functions?
Circular functions, also known as trigonometric functions, are fundamental in mathematics. They describe relationships between angles and sides of triangles, especially right-angled ones. Let's dive into some fascinating facts about these functions.
-
Sine, Cosine, and Tangent are the primary circular functions. They are often abbreviated as sin, cos, and tan.
-
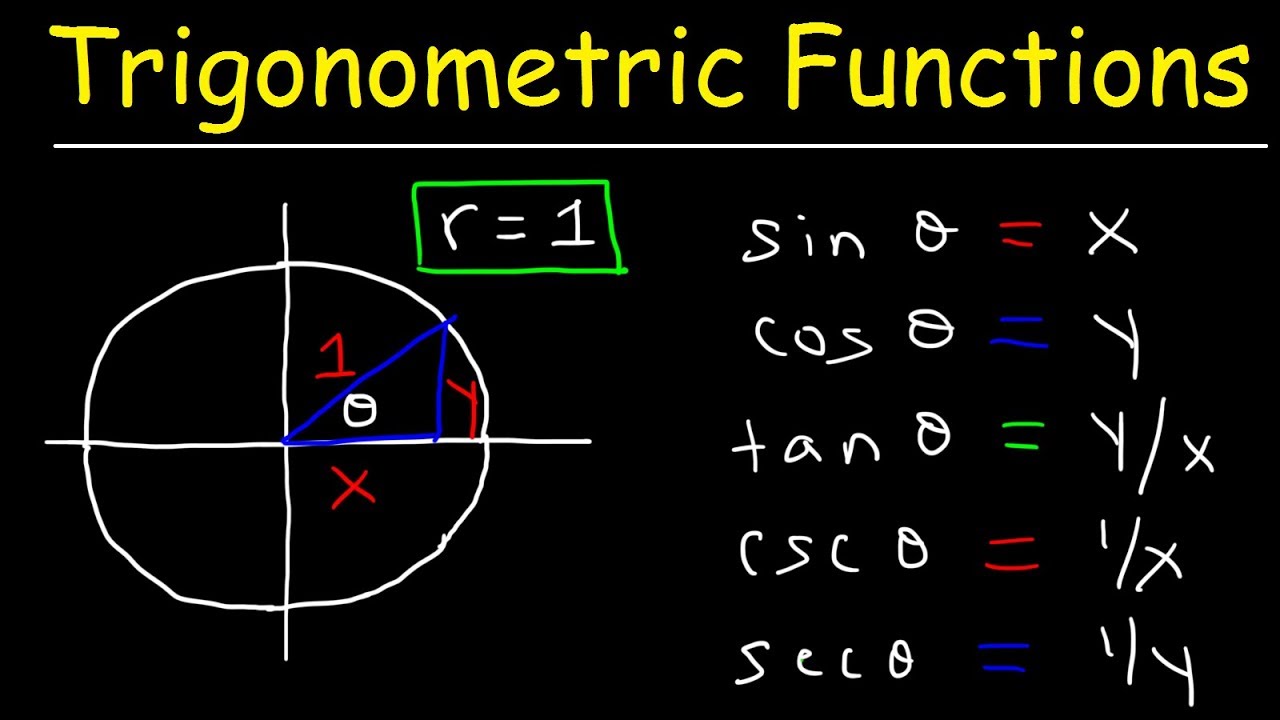
Unit Circle: Circular functions are defined using the unit circle, a circle with a radius of one centered at the origin of a coordinate plane.
-
Radians: Angles in circular functions are often measured in radians. One full circle is (2pi) radians.
-
Periodic Nature: Sine and cosine functions are periodic with a period of (2pi), meaning they repeat every (2pi) radians.
-
Amplitude: The maximum value of sine and cosine functions is 1, and the minimum is -1. This range is called the amplitude.
Historical Background
Understanding the history of circular functions can provide context for their development and use in various fields.
-
Ancient Origins: The study of trigonometric functions dates back to ancient civilizations like the Greeks and Indians.
-
Hipparchus: Often called the "father of trigonometry," Hipparchus created the first known trigonometric table.
-
Ptolemy: Ptolemy expanded on Hipparchus's work and developed the Ptolemaic system, which used trigonometry to describe planetary motions.
-
Indian Mathematicians: Indian scholars like Aryabhata and Brahmagupta made significant contributions to trigonometry, including early forms of sine and cosine.
Applications in Real Life
Circular functions are not just theoretical; they have practical applications in various fields.
-
Engineering: Engineers use trigonometric functions to design and analyze structures, from bridges to skyscrapers.
-
Physics: In physics, circular functions describe wave motion, oscillations, and harmonic motion.
-
Astronomy: Astronomers use trigonometry to calculate distances between celestial bodies and predict their movements.
-
Music: Sound waves are modeled using sine and cosine functions, helping in the analysis of musical tones.
Mathematical Properties
Circular functions have unique mathematical properties that make them useful in solving various problems.
-
Pythagorean Identity: One of the fundamental identities is (sin^2(x) + cos^2(x) = 1).
-
Even and Odd Functions: Cosine is an even function ((cos(-x) = cos(x))), while sine is an odd function ((sin(-x) = -sin(x))).
-
Inverse Functions: The inverse functions of sine, cosine, and tangent are arcsine, arccosine, and arctangent, respectively.
-
Addition Formulas: There are specific formulas for the sine and cosine of the sum of two angles, such as (sin(a + b) = sin(a)cos(b) + cos(a)sin(b)).
Graphical Representations
Visualizing circular functions helps in understanding their behavior and properties.
-
Sine Wave: The graph of the sine function is a smooth, continuous wave that oscillates between -1 and 1.
-
Cosine Wave: Similar to the sine wave, the cosine wave also oscillates between -1 and 1 but starts at its maximum value.
-
Tangent Curve: The tangent function has a different graph, with vertical asymptotes where the function is undefined.
-
Phase Shift: Circular function graphs can be shifted horizontally, known as phase shifts, which are crucial in signal processing.
Advanced Concepts
For those delving deeper into mathematics, circular functions offer more complex and intriguing aspects.
-
Fourier Series: Circular functions are used in Fourier series to represent periodic functions as sums of sines and cosines.
-
Complex Numbers: Euler's formula, (e^{ix} = cos(x) + isin(x)), connects circular functions with complex numbers.
-
Hyperbolic Functions: Hyperbolic sine and cosine functions, (sinh) and (cosh), are analogs of the circular functions but for hyperbolas.
-
Differential Equations: Solutions to many differential equations involve circular functions, especially in physics and engineering.
Fun Facts
Circular functions also have some quirky and fun aspects that make them interesting.
-
Mnemonics: "SOH-CAH-TOA" is a popular mnemonic to remember the definitions of sine, cosine, and tangent.
-
Pi Day: Celebrated on March 14th (3/14), Pi Day often involves activities related to circular functions and the number (pi).
-
Graphing Calculators: Modern graphing calculators can plot circular functions, making it easier for students to visualize and understand them.
The Final Word on Circular Functions
Circular functions, or trigonometric functions, are essential in mathematics and science. They help us understand angles, waves, and rotations. Sine, cosine, and tangent are the main players, each with unique properties and applications. These functions appear in geometry, physics, engineering, and even music. They help us model periodic phenomena like sound waves and light waves. Understanding them can make complex problems simpler and more intuitive. Whether you're a student, teacher, or just curious, knowing these functions opens up a world of possibilities. So, next time you see a wave or a circle, remember the math behind it. Circular functions are more than just numbers; they're a key to understanding the world around us. Keep exploring, keep questioning, and let these functions guide your way.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
