39 Facts About Geometric Phase

What is Geometric Phase?

Geometric phase, also known as Berry phase, is a fascinating concept in quantum mechanics and other areas of physics. It describes how a system's phase changes due to its geometric properties rather than its dynamic properties. Let's dive into some intriguing facts about this phenomenon.

1. Geometric phase was first introduced by Sir Michael Berry in 1984. He discovered that when a quantum system undergoes adiabatic (slow) evolution and returns to its initial physical state, its wave function can acquire a phase factor dependent on the path taken.

2. The concept isn't limited to quantum mechanics. It also appears in classical mechanics, optics, and even in the study of molecular structures.

3. Berry phase can be observed in polarized light. When light passes through a series of optical elements, its polarization state can acquire a geometric phase.

4. Geometric phase is a global property. Unlike dynamic phase, which depends on the time evolution of the system, geometric phase depends on the entire path taken by the system in its parameter space.

5. It plays a crucial role in quantum computing. Geometric phase can be used to create robust quantum gates that are less sensitive to errors.

6. Berry phase has applications in condensed matter physics. It helps explain phenomena like the quantum Hall effect and topological insulators.

7. The concept can be extended to non-adiabatic processes. This extension is known as the Aharonov-Anandan phase.

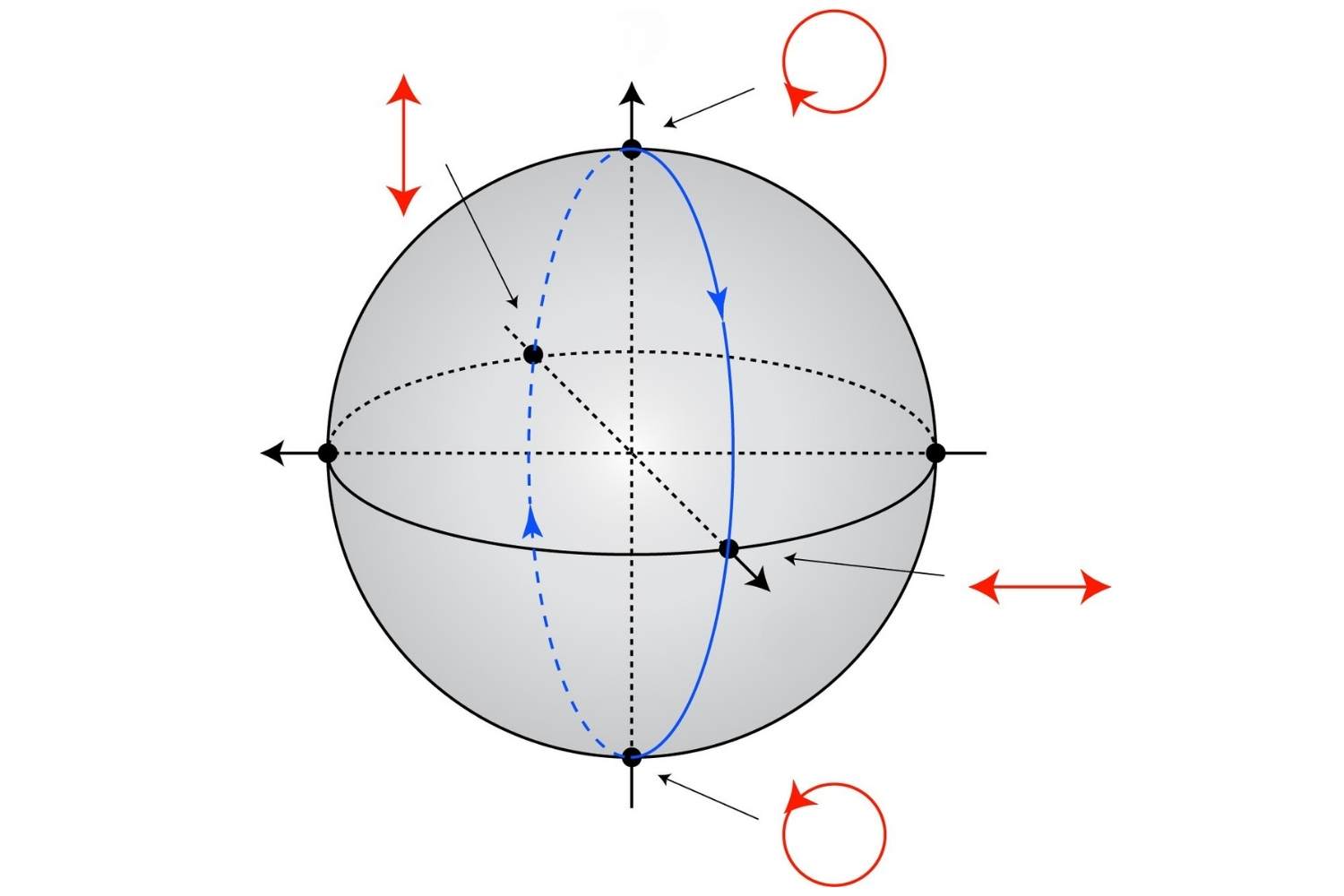
8. Geometric phase can be visualized using the Bloch sphere. For a two-level quantum system, the phase can be represented as the area enclosed by the path on the Bloch sphere.

9. It has a counterpart in classical mechanics called Hannay's angle. This describes the phase shift in classical systems undergoing cyclic adiabatic processes.

10. Geometric phase is gauge-invariant. This means it remains unchanged under certain transformations, making it a fundamental property of the system.

Historical Milestones in Geometric Phase

Understanding the historical context of geometric phase helps appreciate its significance. Here are some key milestones.

11. The concept of phase in wave mechanics dates back to the 19th century. Early studies focused on the dynamic phase associated with wave propagation.

12. In 1956, Pancharatnam introduced a similar concept in optics. He showed that the phase difference between two polarized light beams depends on their geometric arrangement.

13. Berry's 1984 paper was a breakthrough. It unified various observations under a single theoretical framework, sparking widespread interest.

14. The 1990s saw the development of non-adiabatic geometric phases. Researchers like Aharonov and Anandan extended Berry's ideas to more general settings.

15. In 2003, the concept of geometric phase was experimentally verified in quantum systems. This provided concrete evidence for its existence and practical relevance.

16. Recent advances have linked geometric phase to topological properties. This has opened new avenues in the study of topological phases of matter.

Applications of Geometric Phase

Geometric phase isn't just a theoretical curiosity; it has practical applications across various fields.

17. In quantum computing, geometric phase helps create fault-tolerant gates. These gates are less prone to errors, making them ideal for robust quantum computations.

18. Optical systems use geometric phase for beam shaping. Devices like q-plates can manipulate light beams based on their geometric phase properties.

19. Geometric phase plays a role in molecular chemistry. It helps explain the behavior of molecules during chemical reactions.

20. In condensed matter physics, it aids in understanding topological insulators. These materials have unique properties that are protected by their geometric phase.

21. Geometric phase is used in interferometry. It enhances the precision of measurements in devices like gyroscopes and accelerometers.

22. In acoustics, geometric phase helps design better sound systems. It can be used to control the phase of sound waves for improved audio quality.

23. Geometric phase has applications in robotics. It helps in the control and stabilization of robotic systems.

24. In electronics, it aids in the design of phase shifters. These components are crucial for communication systems.

25. Geometric phase is used in the study of biological systems. It helps understand processes like protein folding and DNA replication.

Mathematical Foundations of Geometric Phase

The mathematical framework behind geometric phase is both elegant and complex. Here are some key aspects.

26. Geometric phase is described using differential geometry. This branch of mathematics deals with curves, surfaces, and their properties.

27. The concept of holonomy is central to geometric phase. Holonomy describes how vectors change when transported around a closed loop.

28. Berry phase can be calculated using the Berry connection. This mathematical object encodes information about the system's geometric properties.

29. The Berry curvature is another important concept. It describes how the geometric phase changes with respect to the system's parameters.

30. Geometric phase can be represented using path integrals. This approach sums over all possible paths the system can take, providing a comprehensive description.

31. In quantum mechanics, geometric phase is related to the wave function's phase. This phase can be extracted using techniques like interferometry.

32. Geometric phase has a topological interpretation. It can be linked to topological invariants, which are quantities that remain unchanged under continuous deformations.

33. The mathematical formalism of geometric phase is closely related to gauge theory. Gauge theory describes how fields interact with particles, providing a unified framework for various physical phenomena.

Experimental Observations of Geometric Phase

Experimental verification of geometric phase has been crucial in establishing its validity. Here are some notable experiments.

34. In 1986, the first experimental observation of Berry phase was reported. This involved neutron interferometry, where the phase shift of neutrons was measured.

35. Experiments with polarized light have demonstrated geometric phase. These experiments use optical elements to manipulate the polarization state of light.

36. In 2003, geometric phase was observed in superconducting qubits. This provided evidence for its relevance in quantum computing.

37. Experiments with cold atoms have shown geometric phase effects. These systems allow precise control over the atoms' parameters, making them ideal for studying geometric phase.

38. Geometric phase has been observed in molecular systems. Techniques like nuclear magnetic resonance (NMR) have been used to measure the phase shift in molecules.

39. Recent experiments have linked geometric phase to topological properties. These studies have provided new insights into the behavior of topological materials.

Final Thoughts on Geometric Phases

Geometric phases might seem complex, but they’re fascinating once you get the hang of them. These phases pop up in various fields like physics, chemistry, and even computer science. They help explain phenomena like the Aharonov-Bohm effect and the Berry phase, which are crucial for understanding quantum mechanics.

Knowing about geometric phases can deepen your appreciation for the natural world and the intricate dance of particles and waves. They’re not just theoretical; they have practical applications in technologies like quantum computing and molecular dynamics.

So, next time you hear about geometric phases, you’ll know they’re more than just abstract concepts. They’re a key part of the puzzle that makes up our universe. Keep exploring, and who knows what other amazing facts you’ll uncover?