38 Facts About Kronig-Penney Model

What is the Kronig-Penney Model?

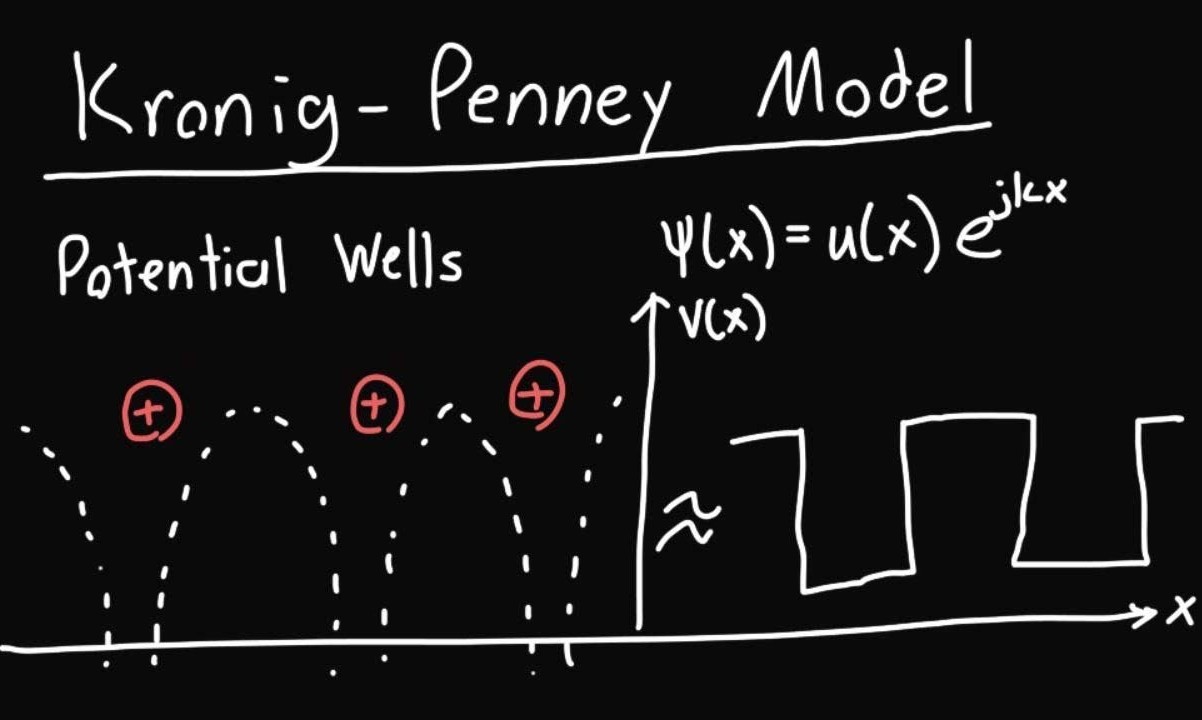
The Kronig-Penney model is a simplified, yet powerful, quantum mechanical model used to describe the behavior of electrons in a periodic potential. It helps explain the electronic band structure of crystalline solids, which is crucial for understanding semiconductors and insulators.

1. The Kronig-Penney model was introduced by Ralph Kronig and William Penney in 1931.
2. It simplifies the complex potential in a crystal lattice to a series of square potential wells.
3. This model is a one-dimensional representation, making it easier to solve mathematically.
4. It provides insight into the formation of energy bands and band gaps in solids.
5. The model assumes an infinite periodic potential, which is not entirely realistic but useful for theoretical purposes.

Importance in Solid-State Physics

Understanding the Kronig-Penney model is essential for anyone studying solid-state physics or materials science. It lays the groundwork for more complex theories and applications.

6. It helps explain why materials can be conductors, semiconductors, or insulators.
7. The model shows how electrons can move through a crystal lattice.
8. It introduces the concept of allowed and forbidden energy bands.
9. The Kronig-Penney model is often the first step in learning about more complex band structure calculations.
10. It provides a basis for understanding the behavior of electrons in various materials.

Mathematical Foundation

The Kronig-Penney model relies on solving Schrödinger's equation for a periodic potential. This involves some intricate mathematics, but the results are highly informative.

11. Schrödinger's equation is a fundamental equation in quantum mechanics.
12. The periodic potential in the model is represented by a series of delta functions or square wells.
13. Solving the equation involves applying boundary conditions at the edges of the potential wells.
14. The solutions to the equation are wave functions that describe the probability of finding an electron in a given position.
15. These wave functions must be continuous and differentiable at the boundaries of the potential wells.

Energy Bands and Band Gaps

One of the most significant outcomes of the Kronig-Penney model is the formation of energy bands and band gaps, which are crucial for understanding electronic properties of materials.

16. Energy bands are ranges of energy that electrons can occupy in a solid.
17. Band gaps are ranges of energy where no electron states can exist.
18. The width of the band gap determines whether a material is a conductor, semiconductor, or insulator.
19. In conductors, the valence band overlaps with the conduction band, allowing free movement of electrons.
20. In semiconductors, there is a small band gap that can be overcome by thermal energy or doping.
21. Insulators have a large band gap, preventing electron flow under normal conditions.

Applications in Modern Technology

The principles derived from the Kronig-Penney model have numerous applications in modern technology, particularly in the development of electronic devices.

22. It is fundamental in the design of semiconductors used in computers and smartphones.
23. The model helps in understanding the behavior of transistors, which are the building blocks of modern electronics.
24. It aids in the development of photovoltaic cells used in solar panels.
25. The principles are applied in the creation of light-emitting diodes (LEDs).
26. It is also used in the study of nanomaterials and quantum dots.

Limitations and Extensions

While the Kronig-Penney model is highly useful, it has its limitations. However, these limitations have led to the development of more advanced models.

27. The model assumes a one-dimensional lattice, which is an oversimplification of real crystals.
28. It does not account for electron-electron interactions.
29. The potential wells are assumed to be infinitely deep, which is not realistic.
30. Despite these limitations, the model provides a good approximation for many purposes.
31. More advanced models, like the nearly free electron model and tight-binding model, build on the principles of the Kronig-Penney model.

Historical Context and Impact

The introduction of the Kronig-Penney model marked a significant milestone in the field of quantum mechanics and solid-state physics.

32. It was one of the first models to successfully explain the electronic properties of solids.
33. The model played a crucial role in the development of quantum theory.
34. It has been cited in numerous scientific papers and textbooks.
35. The principles of the model are still taught in physics and engineering courses today.
36. It has inspired further research and development in the field of condensed matter physics.

Fun Facts

Here are some interesting tidbits about the Kronig-Penney model that you might find intriguing.

37. Ralph Kronig was a student of the famous physicist Arnold Sommerfeld.
38. William Penney later became a key figure in the development of the British atomic bomb.

The Kronig-Penney model, despite its simplicity, remains a cornerstone in the understanding of electronic properties in materials. Its impact on both theoretical and applied physics continues to be profound.

Final Thoughts on the Kronig-Penney Model

The Kronig-Penney model is a cornerstone in solid-state physics. It simplifies complex quantum mechanics problems, making it easier to understand electron behavior in crystal lattices. This model has paved the way for advancements in semiconductor technology, quantum computing, and material science. By breaking down potential barriers into a series of square wells, it provides a clear framework for studying band structures and energy gaps.

Understanding this model isn't just for physicists; it has practical applications in everyday technology, from smartphones to solar panels. The Kronig-Penney model continues to be a valuable tool for researchers and engineers alike. Whether you're a student, a professional, or just curious, grasping the basics of this model can offer deeper insights into the quantum world and its impact on modern technology.