37 Facts About Renormalization Group Theory

What is Renormalization Group Theory?

Renormalization Group Theory (RGT) is a mathematical framework used in physics to study changes in physical systems as they are observed at different scales. It has applications in quantum field theory, statistical mechanics, and condensed matter physics. Here are some fascinating facts about this theory.

1. Origin: RGT was developed in the 1950s and 1960s by physicists like Murray Gell-Mann, Kenneth Wilson, and Leo Kadanoff.

2. Scale Invariance: The theory helps explain why certain physical systems exhibit the same behavior at different scales.

3. Critical Phenomena: RGT is crucial for understanding critical phenomena, such as phase transitions in materials.

4. Quantum Field Theory: It plays a significant role in quantum field theory, helping to make sense of infinite quantities that arise in calculations.

5. Condensed Matter Physics: RGT is used to study properties of materials, including superconductors and magnets.

Key Concepts in Renormalization Group Theory

Understanding the core concepts of RGT can be complex, but breaking them down makes it easier to grasp.

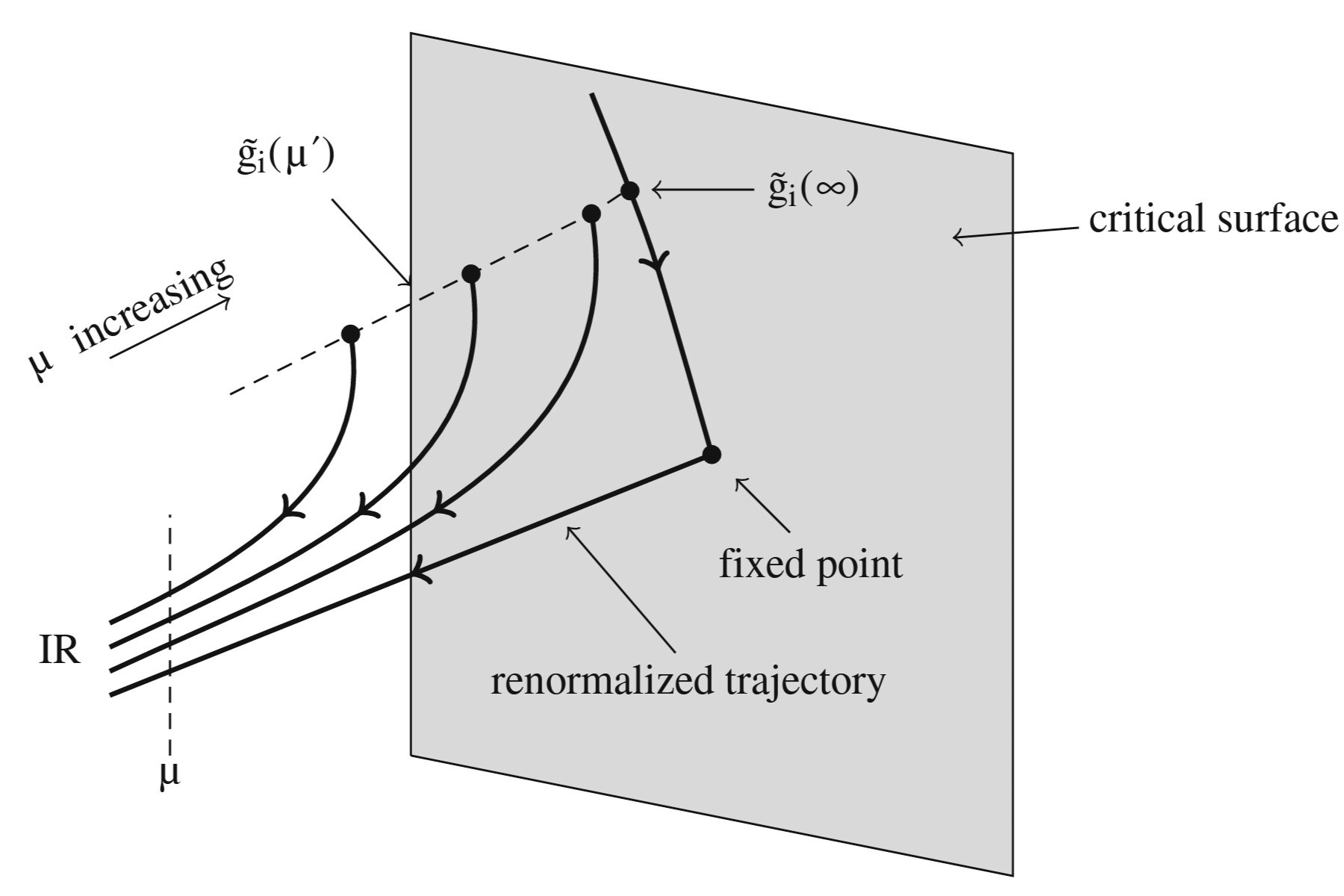
6. Fixed Points: These are points in the parameter space where the system's behavior does not change under scale transformations.

7. Flow Equations: These equations describe how parameters change as the scale changes.

8. Universality: Different systems can exhibit the same critical behavior, a concept known as universality.

9. Dimensional Analysis: RGT often involves dimensional analysis to understand how physical quantities scale.

10. Effective Field Theory: This is a related concept where only relevant degrees of freedom are considered at a given scale.

Applications of Renormalization Group Theory

RGT is not just a theoretical construct; it has practical applications in various fields of physics.

11. Particle Physics: Helps in understanding the behavior of fundamental particles at different energy scales.

12. Statistical Mechanics: Used to study systems with a large number of degrees of freedom, like gases and liquids.

13. Critical Exponents: RGT helps calculate critical exponents, which describe how physical quantities diverge near critical points.

14. Lattice Models: Used in the study of lattice models in condensed matter physics.

15. Quantum Chromodynamics: RGT is essential for understanding the strong force in quantum chromodynamics.

Historical Milestones

The development of RGT has been marked by several key milestones.

16. 1950s: Initial ideas about scale invariance and critical phenomena began to take shape.

17. 1960s: Leo Kadanoff introduced the concept of block spins, a precursor to modern RGT.

18. 1971: Kenneth Wilson formulated the modern RGT, earning him a Nobel Prize in Physics in 1982.

19. 1980s: RGT became a standard tool in theoretical physics, with applications expanding to various fields.

20. 2000s: Advances in computational methods have allowed for more precise calculations using RGT.

Mathematical Foundations

The mathematical underpinnings of RGT are both intricate and fascinating.

21. Differential Equations: RGT often involves solving complex differential equations.

22. Perturbation Theory: Used to handle small deviations from known solutions.

23. Functional Integrals: These integrals are used to sum over all possible configurations of a system.

24. Scaling Laws: Mathematical expressions that describe how physical quantities change with scale.

25. Eigenvalues and Eigenvectors: Important in understanding the stability of fixed points.

Challenges and Limitations

Despite its power, RGT has its challenges and limitations.

26. Computational Complexity: Calculations can be extremely complex and require significant computational resources.

27. Approximation Methods: Often, approximations are needed, which can introduce errors.

28. Non-perturbative Effects: Some phenomena cannot be captured by perturbative methods.

29. High-Dimensional Systems: RGT can be less effective for systems with many interacting components.

30. Experimental Verification: Some predictions of RGT are difficult to verify experimentally.

Future Directions

The future of RGT looks promising, with ongoing research and new applications emerging.

31. Machine Learning: Combining RGT with machine learning to analyze complex systems.

32. Quantum Computing: Using quantum computers to perform RGT calculations more efficiently.

33. Biological Systems: Applying RGT to understand complex biological systems.

34. Cosmology: Using RGT to study the early universe and cosmic inflation.

35. Material Science: Developing new materials with desired properties using insights from RGT.

Fun Facts

Here are some lighter, intriguing tidbits about RGT.

36. Nobel Prize: Kenneth Wilson's Nobel Prize in 1982 highlighted the importance of RGT in modern physics.

37. Interdisciplinary: RGT's concepts are so versatile they are used in fields as diverse as economics and sociology.

The Power of Renormalization Group Theory

Renormalization Group Theory (RGT) is a cornerstone in modern physics. It helps scientists understand how physical systems behave at different scales. From quantum field theory to statistical mechanics, RGT provides a framework for tackling complex problems. Its applications extend beyond physics, influencing areas like chemistry and even finance.

Understanding RGT can be challenging, but its impact is undeniable. It has revolutionized our approach to studying critical phenomena and phase transitions. By simplifying complex interactions, RGT allows for more accurate predictions and deeper insights.

Whether you're a student, researcher, or just curious, grasping the basics of RGT can open up new perspectives. It's a powerful tool that continues to shape our understanding of the universe. So, dive in, explore, and let the wonders of Renormalization Group Theory expand your horizons.