37 Facts About Aharonov-Anandan Phase

What is the Aharonov-Anandan Phase?

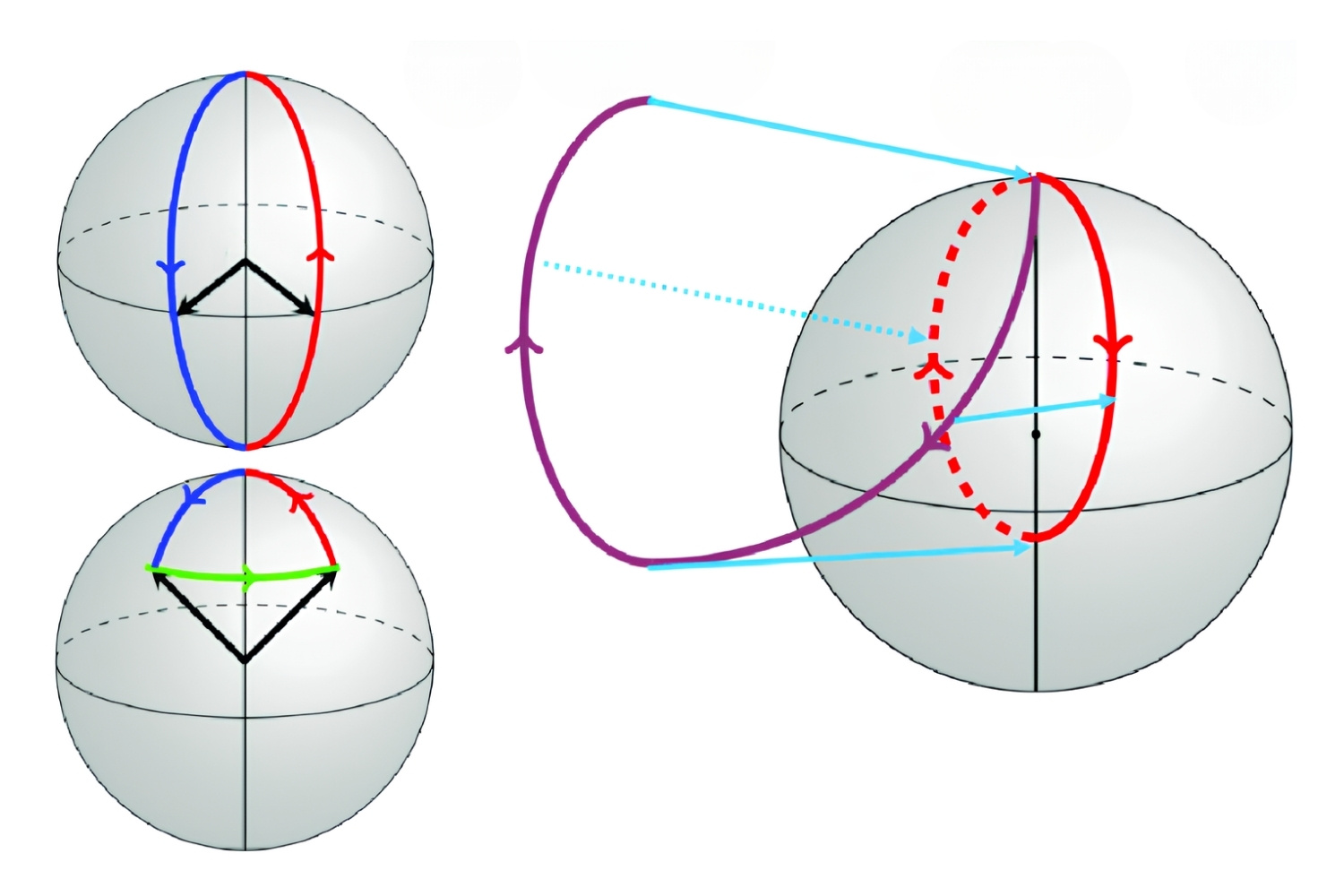
The Aharonov-Anandan phase is a concept in quantum mechanics that extends the idea of the geometric phase. It was introduced by Yakir Aharonov and Jeeva Anandan in 1987. This phase is observed when a quantum system undergoes cyclic evolution, even if the evolution is not adiabatic.

1. The Aharonov-Anandan phase generalizes the Berry phase, which is limited to adiabatic processes.
2. It is a geometric phase, meaning it depends only on the path taken by the system's state in its projective Hilbert space.
3. Unlike the Berry phase, the Aharonov-Anandan phase does not require the system to be in a slowly changing Hamiltonian.
4. This phase can be observed in systems with cyclic evolution, where the system returns to its initial state after some time.
5. The concept is crucial for understanding quantum systems that do not adhere to adiabatic conditions.

Historical Background

Understanding the historical context of the Aharonov-Anandan phase helps appreciate its significance in quantum mechanics.

6. Yakir Aharonov and Jeeva Anandan introduced this phase in a 1987 paper published in Physical Review Letters.
7. The idea was inspired by the earlier work of Michael Berry, who introduced the Berry phase in 1984.
8. Aharonov and Anandan aimed to generalize Berry's work to non-adiabatic processes.
9. Their work has since been cited in numerous studies, highlighting its importance in quantum mechanics.
10. The Aharonov-Anandan phase has applications in various fields, including quantum computing and quantum information theory.

Mathematical Formulation

The mathematical formulation of the Aharonov-Anandan phase provides a rigorous framework for understanding this concept.

11. The phase is given by the integral of the connection one-form over a closed loop in the projective Hilbert space.
12. Mathematically, it can be expressed as (gamma = oint_C langle psi | dpsi rangle), where (|psirangle) is the state vector.
13. This integral is path-dependent, meaning the phase depends on the trajectory taken by the state vector.
14. The phase is gauge-invariant, implying it remains unchanged under local gauge transformations.
15. The Aharonov-Anandan phase can be calculated for any cyclic evolution, regardless of the Hamiltonian's nature.

Physical Interpretation

Understanding the physical interpretation of the Aharonov-Anandan phase helps in grasping its implications in real-world systems.

16. The phase represents a shift in the quantum state's phase due to its geometric properties.
17. It can be observed in systems undergoing cyclic evolution, such as particles in a magnetic field.
18. The phase is independent of the time taken for the evolution, focusing solely on the path in the projective Hilbert space.
19. This phase can lead to observable effects, such as shifts in interference patterns in quantum experiments.
20. The Aharonov-Anandan phase has been experimentally verified in various systems, including optical and atomic setups.

Applications in Quantum Computing

The Aharonov-Anandan phase has significant applications in the field of quantum computing, offering new avenues for research and development.

21. It can be used to design fault-tolerant quantum gates, essential for robust quantum computing.
22. The phase provides a way to implement geometric quantum computation, which is less sensitive to certain types of errors.
23. Quantum algorithms can leverage this phase to perform specific tasks more efficiently.
24. The Aharonov-Anandan phase can help in developing new quantum error correction codes.
25. Researchers are exploring its use in topological quantum computing, which aims to create more stable qubits.

Experimental Observations

Experimental observations of the Aharonov-Anandan phase have validated its theoretical predictions and expanded our understanding of quantum mechanics.

26. The phase has been observed in optical systems using polarized light.
27. Experiments with trapped ions have demonstrated the phase in atomic systems.
28. Superconducting qubits have been used to study the Aharonov-Anandan phase in solid-state systems.
29. The phase has been measured in interferometry experiments, where it causes shifts in interference patterns.
30. These observations confirm the phase's existence and its dependence on the geometric properties of the quantum system.

Future Research Directions

Future research on the Aharonov-Anandan phase promises to uncover new insights and applications in quantum mechanics and beyond.

31. Researchers are exploring its role in quantum entanglement and coherence.
32. The phase could provide new ways to manipulate quantum states for advanced technologies.
33. Studies are investigating its implications for quantum thermodynamics and energy transfer.
34. The Aharonov-Anandan phase may offer new perspectives on the foundations of quantum mechanics.
35. Ongoing research aims to develop practical applications, such as quantum sensors and communication systems.
36. The phase's geometric nature could inspire new mathematical frameworks for quantum theory.
37. Collaborative efforts between theorists and experimentalists will continue to push the boundaries of our understanding of the Aharonov-Anandan phase.

Final Thoughts on Aharonov-Anandan Phase

The Aharonov-Anandan phase is a fascinating concept in quantum mechanics. It reveals how a system's state can evolve over time, even without a traditional path. This phase helps scientists understand quantum systems better, offering insights into quantum computing and quantum communication.

Understanding this phase isn't just for physicists. It has practical applications in technology, potentially leading to advancements in quantum computers. These computers could solve problems much faster than classical ones, revolutionizing fields like cryptography and complex simulations.

The Aharonov-Anandan phase shows how quantum mechanics continues to surprise and challenge our understanding of the universe. By grasping these concepts, we can appreciate the intricate dance of particles and waves that make up our reality. Keep exploring, and who knows what other quantum mysteries we'll uncover next!