35 Facts About Friedmann Equations

What Are Friedmann Equations?

Friedmann equations are fundamental in cosmology, describing how the universe expands. Named after Alexander Friedmann, these equations stem from Einstein's field equations of general relativity. They help scientists understand the dynamics of the cosmos.

1. Origin: Alexander Friedmann, a Russian physicist, derived these equations in 1922 and 1924.

2. Einstein's Reluctance: Initially, Einstein doubted Friedmann's work, believing the universe was static.

3. Two Equations: There are two main Friedmann equations, both crucial for cosmological models.

4. General Relativity: These equations are solutions to Einstein's field equations in general relativity.

5. Cosmological Constant: The equations can include a cosmological constant, representing dark energy.

Components of Friedmann Equations

Understanding the components of these equations helps grasp their significance. They involve various parameters that describe the universe's expansion.

6. Scale Factor: This factor measures how distances in the universe change over time.

7. Hubble Parameter: It describes the rate of expansion of the universe.

8. Density Parameters: These parameters include matter density, radiation density, and dark energy density.

9. Curvature Parameter: Indicates whether the universe is open, closed, or flat.

10. Pressure: The pressure of different components like radiation and matter affects the universe's expansion.

Importance in Cosmology

Friedmann equations are pivotal in modern cosmology, providing insights into the universe's past, present, and future.

11. Big Bang Theory: They support the Big Bang theory, explaining the universe's origin from a singularity.

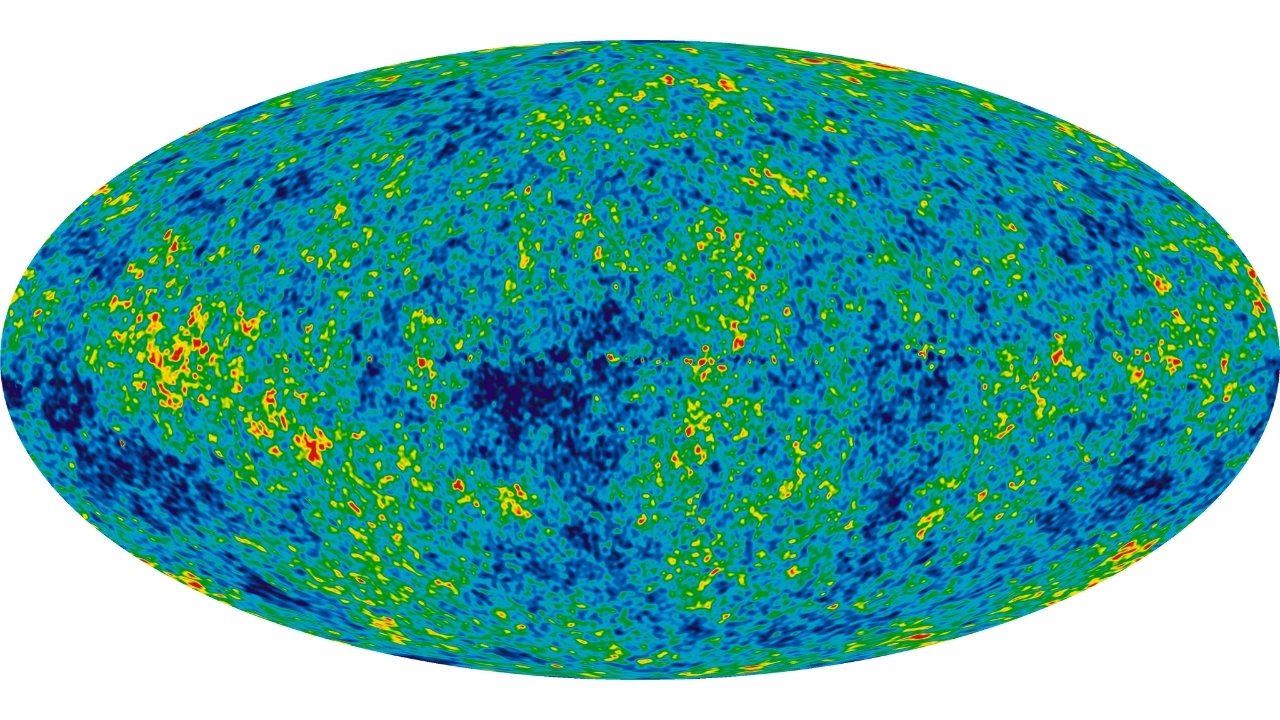
12. Cosmic Microwave Background: These equations help interpret the cosmic microwave background radiation.

13. Dark Energy: They offer a framework to study dark energy's role in accelerating the universe's expansion.

14. Structure Formation: The equations explain how galaxies and large-scale structures form over time.

15. Cosmic Age: They help estimate the age of the universe.

Observational Evidence

Observations and experiments validate the predictions made by Friedmann equations, reinforcing their importance.

16. Redshift: Observations of redshift in distant galaxies support the universe's expansion.

17. Supernovae: Type Ia supernovae observations confirm the accelerating expansion of the universe.

18. Cosmic Microwave Background: Measurements of the cosmic microwave background align with predictions from these equations.

19. Galaxy Clusters: The distribution and movement of galaxy clusters provide evidence for the equations.

20. Gravitational Lensing: Observations of gravitational lensing support the universe's expansion described by these equations.

Mathematical Formulation

The mathematical formulation of Friedmann equations involves complex calculations, but they can be broken down into simpler terms.

21. First Equation: The first equation relates the universe's expansion rate to its energy content.

22. Second Equation: The second equation describes how the expansion rate changes over time.

23. Energy Density: The equations include terms for different energy densities like matter, radiation, and dark energy.

24. Curvature Term: A term in the equations accounts for the universe's curvature.

25. Cosmological Constant: The equations can include a cosmological constant, representing dark energy.

Historical Context

The historical context of Friedmann equations highlights their development and acceptance in the scientific community.

26. Initial Skepticism: Einstein initially rejected Friedmann's work, but later accepted it after further analysis.

27. Lemaître's Contribution: Georges Lemaître independently derived similar equations, supporting Friedmann's findings.

28. Hubble's Discovery: Edwin Hubble's discovery of the expanding universe provided observational support for these equations.

29. Cold War Era: During the Cold War, Soviet scientists further developed cosmological models based on Friedmann equations.

30. Nobel Prize: Although Friedmann never received a Nobel Prize, his work laid the foundation for future discoveries that did.

Modern Applications

Friedmann equations continue to be relevant in modern cosmology, influencing various research areas.

31. Dark Matter: They help study dark matter's role in the universe's structure and evolution.

32. Inflation Theory: The equations support inflation theory, explaining rapid expansion in the early universe.

33. Multiverse Theory: Some interpretations of these equations suggest the possibility of a multiverse.

34. Quantum Cosmology: They provide a framework for exploring quantum effects in the early universe.

35. Future Predictions: The equations help predict the universe's future, including potential scenarios like the Big Freeze or Big Crunch.

Final Thoughts on Friedmann Equations

Friedmann equations, born from Einstein's general relativity, are key to understanding our universe's expansion. These equations, named after Alexander Friedmann, describe how the universe evolves over time. They help scientists predict the past and future of cosmic expansion, shedding light on phenomena like the Big Bang and dark energy.

Understanding these equations isn't just for physicists. They offer a glimpse into the universe's grand design, showing how everything from galaxies to cosmic microwave background radiation fits together. Whether you're a student, a science enthusiast, or just curious about the cosmos, knowing a bit about Friedmann equations can deepen your appreciation for the universe's complexity.

So next time you gaze at the stars, remember there's a mathematical framework explaining their dance. Friedmann equations are a testament to human curiosity and our quest to understand the cosmos.