35 Facts About Ensemble Theory

What is Ensemble Theory?

Ensemble theory is a fundamental concept in statistical mechanics, a branch of physics that deals with large systems of particles. It helps scientists understand and predict the behavior of systems in equilibrium. Here are some fascinating facts about ensemble theory.

1. Ensemble theory involves studying a large collection of microstates, each representing a possible state of the system.

2. Microstates are specific configurations of particles, including their positions and velocities.

3. Macrostates are defined by macroscopic properties like temperature, pressure, and volume.

4. Ensemble theory bridges the gap between microscopic and macroscopic descriptions of systems.

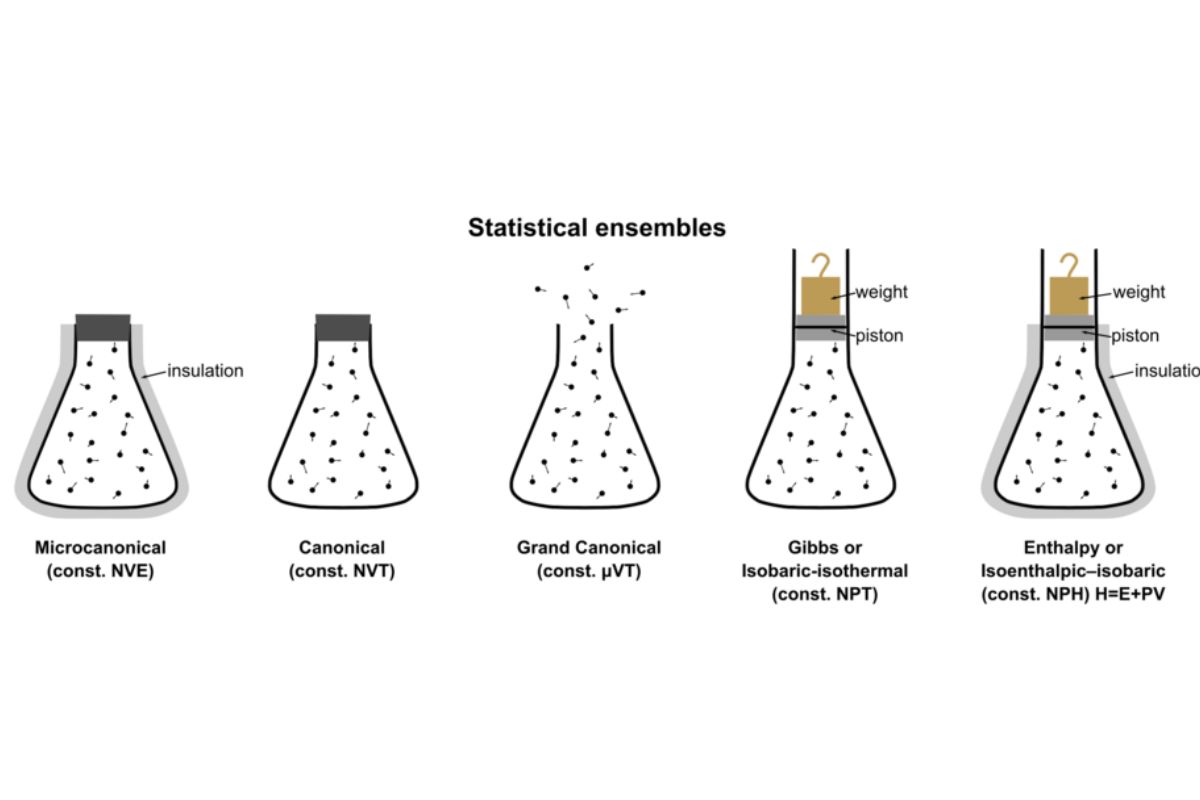
Types of Ensembles

Different types of ensembles are used depending on the conditions of the system being studied. Each type has unique characteristics and applications.

5. Microcanonical Ensemble: This type is used for isolated systems with fixed energy, volume, and particle number.

6. Canonical Ensemble: Used for systems in thermal equilibrium with a heat bath, having fixed temperature, volume, and particle number.

7. Grand Canonical Ensemble: Suitable for systems in contact with a reservoir that can exchange both energy and particles, with fixed temperature, volume, and chemical potential.

8. Isothermal-Isobaric Ensemble: This type is used for systems at constant temperature and pressure, often applied in chemical reactions.

Historical Background

Understanding the history of ensemble theory provides context for its development and significance in modern science.

9. Josiah Willard Gibbs: He introduced the concept of ensembles in the late 19th century, laying the foundation for statistical mechanics.

10. Ludwig Boltzmann: His work on statistical mechanics and entropy paved the way for ensemble theory.

11. James Clerk Maxwell: Contributed to the kinetic theory of gases, which is closely related to ensemble theory.

12. Albert Einstein: Applied statistical mechanics to explain the photoelectric effect and Brownian motion.

Applications in Physics

Ensemble theory has numerous applications in various fields of physics, making it a versatile and powerful tool.

13. Thermodynamics: Helps in understanding the laws of thermodynamics and predicting the behavior of thermodynamic systems.

14. Quantum Mechanics: Used to study quantum systems and predict the behavior of particles at the quantum level.

15. Condensed Matter Physics: Applied to study properties of solids and liquids, including phase transitions and critical phenomena.

16. Astrophysics: Helps in modeling the behavior of stars, galaxies, and other celestial bodies.

Applications in Other Fields

Beyond physics, ensemble theory finds applications in diverse fields, showcasing its wide-ranging utility.

17. Chemistry: Used to study chemical reactions, molecular dynamics, and properties of substances.

18. Biology: Helps in understanding biological systems, including protein folding and cellular processes.

19. Economics: Applied in modeling economic systems and predicting market behavior.

20. Computer Science: Used in algorithms and simulations, particularly in machine learning and artificial intelligence.

Key Concepts in Ensemble Theory

Several key concepts are central to understanding and applying ensemble theory effectively.

21. Partition Function: A mathematical function that encodes information about the statistical properties of a system.

22. Boltzmann Distribution: Describes the probability distribution of particles in different energy states.

23. Ergodic Hypothesis: Assumes that over long periods, a system will explore all accessible microstates.

24. Liouville's Theorem: States that the density of states in phase space remains constant over time.

Challenges and Limitations

Despite its power, ensemble theory has some challenges and limitations that researchers must navigate.

25. Complexity: Analyzing large systems with many particles can be computationally intensive.

26. Approximations: Often requires simplifying assumptions that may not always be accurate.

27. Non-equilibrium Systems: Difficult to apply to systems far from equilibrium, where traditional ensembles may not be valid.

28. Quantum Effects: Incorporating quantum mechanics can add layers of complexity to the analysis.

Future Directions

Ensemble theory continues to evolve, with ongoing research exploring new frontiers and applications.

29. Advanced Simulations: Improved computational methods are enabling more accurate and detailed simulations.

30. Quantum Computing: Potential to revolutionize ensemble theory by solving complex problems more efficiently.

31. Interdisciplinary Research: Increasing collaboration between fields like physics, chemistry, biology, and computer science.

32. Machine Learning: Integration with machine learning techniques to enhance predictive capabilities.

Fun Facts

Here are some lighter, fun facts about ensemble theory that highlight its intriguing aspects.

33. Ensemble Theory in Pop Culture: Concepts from ensemble theory have appeared in science fiction, including movies and TV shows.

34. Educational Tools: Interactive simulations and games are being developed to teach ensemble theory concepts.

35. Nobel Prizes: Several Nobel Prizes in Physics have been awarded for work related to statistical mechanics and ensemble theory.

Final Thoughts on Ensemble Theory

Ensemble theory offers a fascinating glimpse into the world of statistical mechanics and thermodynamics. It helps scientists understand how large systems behave by considering all possible states they can occupy. This approach has practical applications in fields like physics, chemistry, and even computer science. By using ensembles, researchers can predict the properties of materials, understand phase transitions, and develop new technologies.

Understanding the basics of microcanonical, canonical, and grand canonical ensembles can deepen your appreciation for how the microscopic world influences the macroscopic one. These concepts might seem complex at first, but they provide a powerful framework for solving real-world problems.

So, whether you're a student, a researcher, or just someone curious about how the universe works, ensemble theory is a valuable tool. Keep exploring, keep questioning, and who knows? You might just uncover the next big breakthrough.