32 Facts About Period Doubling Bifurcation

What is Period Doubling Bifurcation?

Period doubling bifurcation is a fascinating concept in the field of dynamical systems and chaos theory. It describes a process where a system's periodic behavior changes, leading to a doubling of the period. This phenomenon often serves as a precursor to chaotic behavior.

1. Period doubling bifurcation occurs when a system's periodic orbit splits into two, resulting in a new orbit with twice the period of the original.

2. Mitchell Feigenbaum discovered the universal constants related to period doubling bifurcations in the 1970s, which are now known as Feigenbaum constants.

3. Feigenbaum constants are approximately 4.669 and 2.5029, representing the rate at which period doubling occurs and the scaling factor for the bifurcation intervals.

4. Period doubling can be observed in various systems, including fluid dynamics, electrical circuits, and even biological populations.

5. Chaos theory often begins with period doubling bifurcations, marking the transition from predictable to unpredictable behavior.

How Does Period Doubling Bifurcation Work?

Understanding the mechanics behind period doubling bifurcation can be complex, but breaking it down into simpler facts helps.

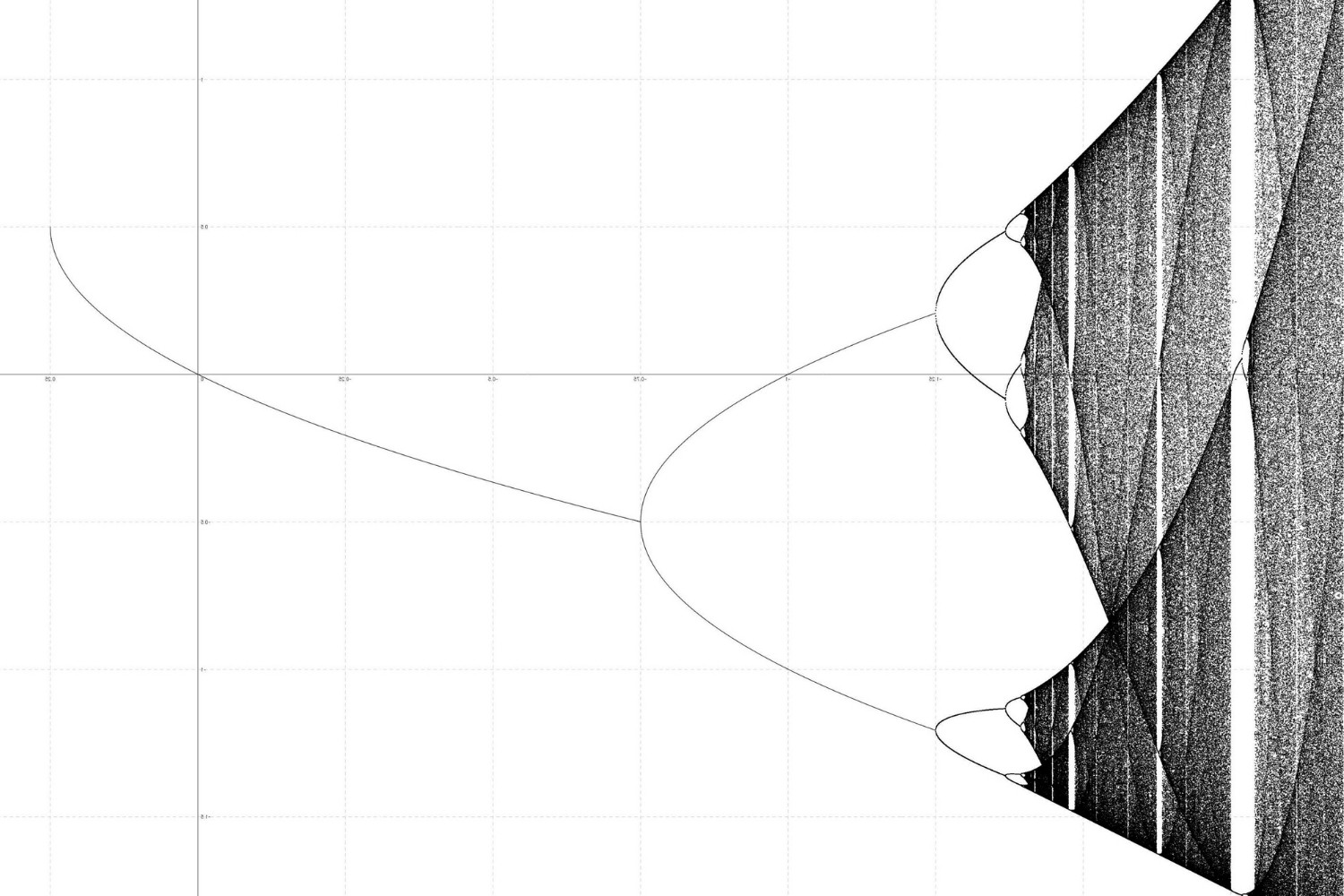
6. Bifurcation diagram is a visual representation showing how a system's behavior changes as a parameter is varied, often revealing period doubling sequences.

7. Logistic map is a common mathematical model used to study period doubling bifurcations, illustrating how population growth can lead to chaotic behavior.

8. Fixed points in a system become unstable during a period doubling bifurcation, leading to the emergence of new periodic orbits.

9. Nonlinear systems are typically where period doubling bifurcations occur, as linear systems do not exhibit such complex behavior.

10. Stability analysis helps determine when a period doubling bifurcation will occur by examining the eigenvalues of the system's Jacobian matrix.

Real-World Examples of Period Doubling Bifurcation

Period doubling bifurcation isn't just a theoretical concept; it has practical applications and can be observed in real-world systems.

11. Heart rhythms can exhibit period doubling bifurcations, leading to arrhythmias and other cardiac issues.

12. Electrical circuits with nonlinear components, such as diodes and transistors, can show period doubling behavior under certain conditions.

13. Fluid dynamics often display period doubling bifurcations, particularly in turbulent flows and convection patterns.

14. Biological populations can experience period doubling bifurcations in their growth cycles, leading to complex population dynamics.

15. Laser systems can exhibit period doubling bifurcations, affecting the stability and output of the laser.

Mathematical Foundations of Period Doubling Bifurcation

The mathematical underpinnings of period doubling bifurcation are crucial for understanding its behavior and implications.

16. Feigenbaum's route to chaos describes the sequence of period doubling bifurcations leading to chaotic behavior in a system.

17. Lyapunov exponents measure the rate of separation of infinitesimally close trajectories, indicating the presence of chaos following period doubling bifurcations.

18. Bifurcation theory studies changes in the qualitative or topological structure of a given family of dynamical systems.

19. Renormalization group theory helps explain the universality of period doubling bifurcations across different systems.

20. Eigenvalues and eigenvectors of the Jacobian matrix are used to analyze the stability of fixed points and periodic orbits in a system.

Historical Context and Discoveries

The history of period doubling bifurcation is rich with discoveries and contributions from various scientists.

21. Mitchell Feigenbaum was a pioneer in the study of period doubling bifurcations, discovering the Feigenbaum constants in the 1970s.

22. Benoît Mandelbrot contributed to the understanding of fractals and chaos, which are closely related to period doubling bifurcations.

23. Edward Lorenz discovered the Lorenz attractor, a chaotic system that exhibits period doubling bifurcations.

24. Henri Poincaré laid the groundwork for modern chaos theory and bifurcation analysis with his studies on dynamical systems.

25. Robert May used the logistic map to study population dynamics, revealing period doubling bifurcations and chaotic behavior.

Applications and Implications

Period doubling bifurcation has numerous applications and implications across various fields of study.

26. Climate models use period doubling bifurcations to understand and predict complex weather patterns and climate changes.

27. Engineering systems often need to account for period doubling bifurcations to ensure stability and avoid chaotic behavior.

28. Economics can exhibit period doubling bifurcations in models of market dynamics and economic cycles.

29. Neuroscience studies period doubling bifurcations to understand brain activity and the onset of epileptic seizures.

30. Robotics uses period doubling bifurcations to improve the stability and performance of autonomous systems.

31. Quantum mechanics explores period doubling bifurcations in the behavior of quantum systems and particles.

32. Artificial intelligence can leverage period doubling bifurcations to enhance machine learning algorithms and optimize performance.

The Fascinating World of Period Doubling Bifurcation

Period doubling bifurcation isn't just a mouthful; it's a gateway to understanding chaos theory. This phenomenon shows how simple systems can evolve into complex, unpredictable behaviors. From the fluttering of a butterfly's wings to stock market fluctuations, period doubling bifurcation helps explain the transition from order to chaos.

Grasping these concepts can deepen your appreciation for the intricate patterns in nature and technology. Whether you're a student, a researcher, or just curious, knowing about period doubling bifurcation can open your eyes to the hidden complexities around us.

So next time you see something that seems random, remember, there might be a fascinating pattern behind it. Dive into the world of chaos theory, and you'll never look at the world the same way again.