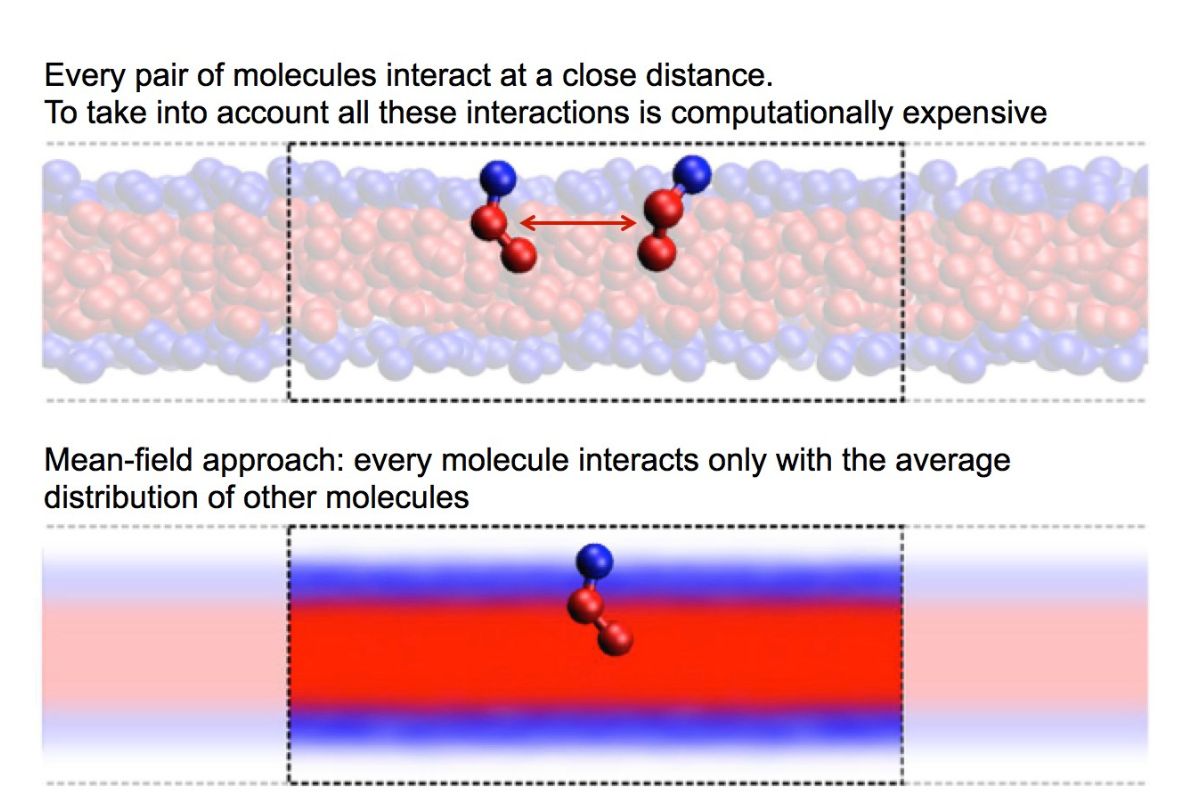
Mean Field Theory is a powerful tool in physics and mathematics used to simplify complex systems by averaging the effects of all individual components. But what exactly is Mean Field Theory? In essence, it approximates the behavior of large, interconnected systems by considering the average effect of all particles or agents, rather than tracking each one individually. This approach helps in understanding phenomena in fields like statistical mechanics, neuroscience, and even economics. Why is it important? Because it allows scientists to make sense of intricate systems that would otherwise be too complicated to analyze. Dive into these 31 fascinating facts about Mean Field Theory to grasp its significance and applications.
What is Mean Field Theory?
Mean Field Theory (MFT) is a mathematical approach used in physics and probability theory to study complex systems. It simplifies the many-body problem by averaging the effect of all other particles on any given particle. This theory has applications in various fields, including physics, biology, and economics. Let's dive into some fascinating facts about Mean Field Theory.
-
Origin in Physics: Mean Field Theory originated in physics, particularly in the study of phase transitions and critical phenomena.
-
Pierre Curie: The theory was first introduced by Pierre Curie in 1895 to explain magnetic properties.
-
Simplification: MFT simplifies complex systems by averaging the interactions, making calculations more manageable.
-
Ising Model: One of the most famous applications is the Ising model, which describes ferromagnetism in statistical mechanics.
-
Phase Transitions: MFT helps in understanding phase transitions, such as the change from liquid to gas or from a magnetized to a non-magnetized state.
-
Critical Temperature: It predicts the critical temperature at which phase transitions occur.
-
Mean Field Approximation: The theory uses a mean field approximation to replace the effect of all other particles with an average effect.
-
Self-Consistent Field: MFT involves solving self-consistent field equations to find the average effect.
-
Applications in Biology: In biology, MFT is used to model the behavior of large populations of interacting organisms.
-
Neural Networks: It is applied in neural networks to understand how neurons interact and process information.
-
Economics: Economists use MFT to model market behavior and predict economic trends.
-
Spin Glasses: MFT is used to study spin glasses, which are disordered magnetic systems.
-
Quantum Field Theory: It has applications in quantum field theory, particularly in understanding particle interactions.
-
Polymer Physics: In polymer physics, MFT helps in studying the behavior of polymer chains.
-
Epidemiology: It is used in epidemiology to model the spread of diseases in large populations.
-
Network Theory: MFT is applied in network theory to study the behavior of large networks, such as social networks or the internet.
-
Computational Simulations: It is often used in computational simulations to reduce the complexity of the system.
-
Mean Field Games: MFT has led to the development of mean field games, which model the behavior of large numbers of interacting agents.
-
Statistical Mechanics: It is a fundamental tool in statistical mechanics for studying many-body systems.
-
Thermodynamics: MFT helps in understanding thermodynamic properties of materials.
-
Critical Exponents: The theory predicts critical exponents, which describe how physical quantities change near the critical point.
-
Landau Theory: It is closely related to Landau theory, which describes phase transitions using an order parameter.
-
Renormalization Group: MFT is a starting point for more advanced techniques like the renormalization group.
-
High-Dimensional Systems: It works particularly well for high-dimensional systems where interactions are averaged out.
-
Finite-Size Effects: MFT can be extended to study finite-size effects in small systems.
-
Stochastic Processes: It is used to model stochastic processes, where randomness plays a significant role.
-
Lattice Models: MFT is applied to lattice models, which describe particles arranged in a regular grid.
-
Percolation Theory: It helps in understanding percolation theory, which studies the movement of fluids through porous materials.
-
Glassy Dynamics: MFT is used to study glassy dynamics, which describe the slow relaxation of disordered systems.
-
Complex Systems: It is a powerful tool for studying complex systems with many interacting components.
-
Future Research: Ongoing research continues to expand the applications and improve the accuracy of Mean Field Theory.
The Final Word on Mean Field Theory
Mean Field Theory (MFT) simplifies complex systems by averaging the effects of all particles, making it easier to study large-scale behaviors. This approach has applications in physics, chemistry, biology, and even economics. By reducing the complexity of interactions, MFT provides insights into phenomena like phase transitions, magnetism, and neural networks.
Understanding MFT helps in grasping how individual components contribute to the overall behavior of a system. It’s a powerful tool for scientists and researchers, offering a clearer picture of intricate processes. While not perfect, MFT remains a cornerstone in theoretical studies, bridging the gap between microscopic interactions and macroscopic observations.
Whether you’re a student, researcher, or just curious, diving into MFT opens up a world of understanding about how the universe operates on both small and large scales. Keep exploring, and you'll uncover even more fascinating aspects of this theory.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
