29 Facts About Tensor Network States

What Are Tensor Network States?

Tensor Network States (TNS) are mathematical structures used in quantum physics and computer science. They help simplify complex quantum systems by breaking them down into smaller, more manageable parts. Let's dive into some fascinating facts about these intriguing constructs.

1. TNS are used to represent quantum states in a more compact form, making calculations easier.

2. They are particularly useful in studying many-body quantum systems, where interactions between particles are complex.

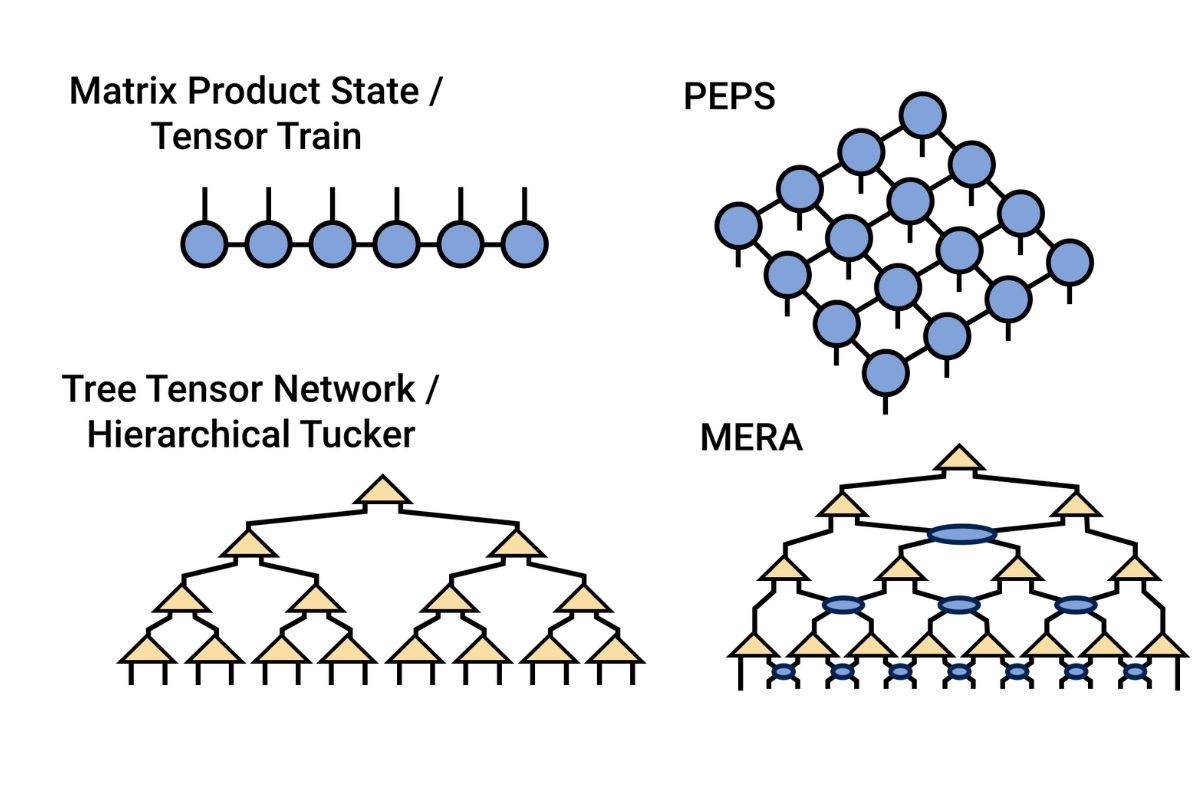
3. TNS can be visualized as networks of interconnected tensors, each representing a small part of the overall system.

4. The most common types of TNS include Matrix Product States (MPS) and Projected Entangled Pair States (PEPS).

5. MPS are often used to study one-dimensional quantum systems, while PEPS are better suited for two-dimensional systems.

6. TNS have applications in quantum computing, where they help optimize algorithms for solving complex problems.

Historical Background of Tensor Network States

Understanding the history of TNS can provide context for their current applications and importance in scientific research.

7. The concept of TNS originated in the 1980s with the development of Density Matrix Renormalization Group (DMRG) methods.

8. DMRG was initially used to study one-dimensional quantum systems, laying the groundwork for modern TNS.

9. In the early 2000s, researchers extended these ideas to higher dimensions, leading to the development of PEPS.

10. The field has grown rapidly, with new types of TNS being proposed and studied regularly.

11. TNS have become a crucial tool in condensed matter physics, helping scientists understand phenomena like superconductivity and quantum phase transitions.

Applications of Tensor Network States

TNS are not just theoretical constructs; they have practical applications in various fields. Here are some ways they are used today.

12. In quantum chemistry, TNS help simulate the behavior of molecules, aiding in the design of new materials and drugs.

13. They are used in machine learning to improve the efficiency of algorithms, particularly in handling large datasets.

14. TNS play a role in quantum error correction, which is essential for building reliable quantum computers.

15. In statistical mechanics, TNS help model systems at thermal equilibrium, providing insights into phase transitions and critical phenomena.

16. They are also used in the study of topological phases of matter, which have potential applications in quantum computing.

Advantages of Using Tensor Network States

Why are TNS so popular in scientific research? Here are some of their key advantages.

17. TNS provide a more efficient representation of quantum states, reducing the computational resources needed for simulations.

18. They allow for the study of larger systems than would be possible with traditional methods.

19. TNS can be adapted to different types of quantum systems, making them versatile tools for researchers.

20. They offer a way to systematically improve approximations, leading to more accurate results.

21. TNS can be used to identify and study emergent phenomena in complex systems.

Challenges and Limitations of Tensor Network States

Despite their many advantages, TNS are not without challenges. Here are some limitations researchers face.

22. Constructing TNS for higher-dimensional systems can be computationally intensive.

23. The accuracy of TNS approximations depends on the specific system being studied, and may not always be reliable.

24. Developing new types of TNS requires a deep understanding of both quantum physics and advanced mathematics.

25. Integrating TNS with other computational methods can be complex and time-consuming.

26. There is ongoing research to improve the scalability of TNS for larger and more complex systems.

Future Directions in Tensor Network States Research

The field of TNS is continually evolving, with new discoveries and applications emerging regularly. Here are some exciting future directions.

27. Researchers are exploring the use of TNS in quantum machine learning, where they could help develop more powerful algorithms.

28. There is interest in using TNS to study non-equilibrium systems, which are not well understood with current methods.

29. Advances in quantum computing may lead to new ways of constructing and using TNS, opening up new possibilities for research and applications.

Final Thoughts on Tensor Network States

Tensor Network States are a powerful tool in quantum physics and computer science. They simplify complex systems, making them easier to understand and manipulate. These states help in solving problems related to quantum entanglement, which is crucial for advancements in quantum computing. By breaking down large systems into smaller, manageable parts, Tensor Network States provide a clearer picture of how particles interact on a quantum level. This has significant implications for developing new technologies and improving existing ones. Researchers continue to explore their potential, aiming to unlock even more applications. Whether you're a student, a professional, or just curious about quantum mechanics, understanding Tensor Network States can offer valuable insights. They represent a fascinating intersection of mathematics, physics, and computer science, opening doors to future innovations. Keep an eye on this field; it's bound to shape the future in exciting ways.