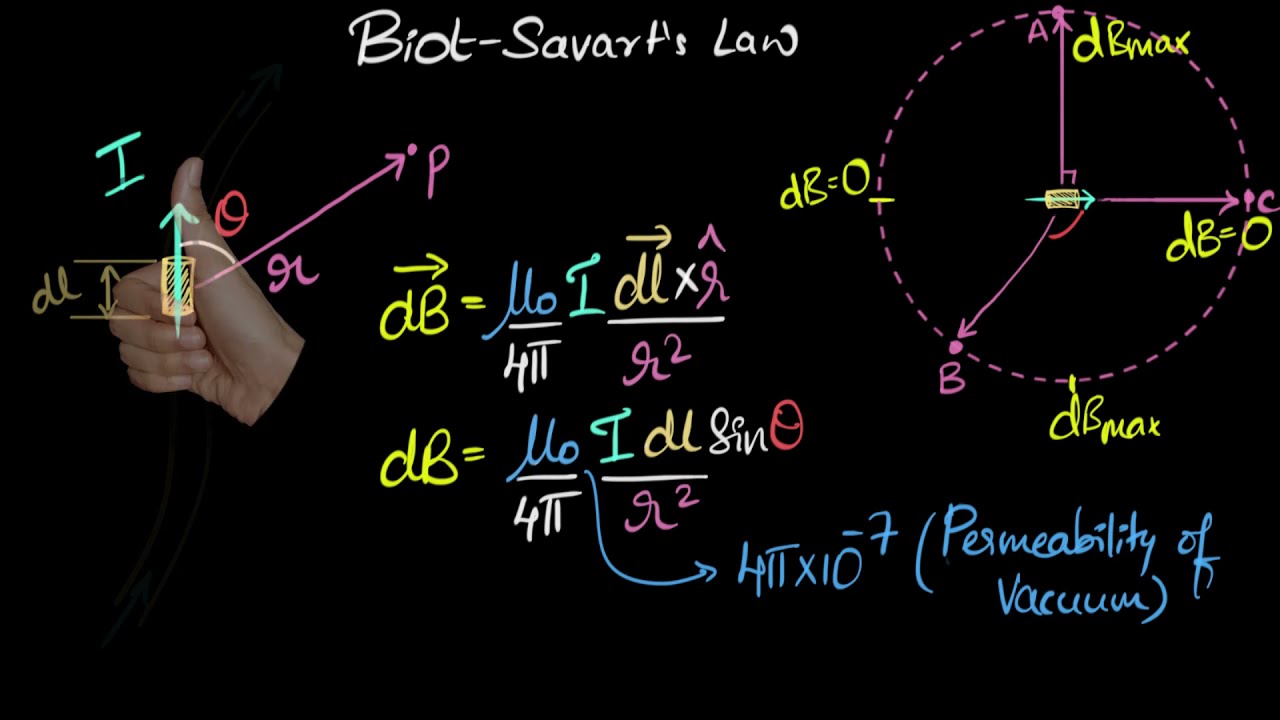
The Biot-Savart Law is a fundamental principle in physics that describes the magnetic field generated by an electric current. Named after the French physicists Jean-Baptiste Biot and Félix Savart, this law has significant applications in various fields such as electromagnetism, magnetostatics, and even astrophysics.
In this article, we will explore 12 extraordinary facts about the Biot-Savart Law, unveiling its importance and shedding light on its fascinating aspects. From its historical origins to its mathematical representation, we will delve into the intricate details of this law and how it governs the behavior of magnetic fields caused by electric currents.
So, whether you are a physics enthusiast or simply curious about the wonders of the universe, join us on this captivating journey as we uncover the intricacies of the Biot-Savart Law and discover why it continues to be an essential part of our understanding of electromagnetism.
Key Takeaways:
- The Biot-Savart Law is a fundamental principle in physics that helps us understand how electric currents create magnetic fields. It’s like a secret code that reveals the hidden magnetism around us!
- By using the Biot-Savart Law, scientists and engineers can unlock the mysteries of magnetic fields and apply this knowledge to power our modern world with devices like transformers, motors, and generators.
Basis of Electromagnetic Theory
The Biot-Savart Law is one of the foundational principles behind electromagnetic theory. It provides a mathematical expression for calculating the magnetic field generated by a small segment of current-carrying wire. This law forms the backbone of many electromagnetism concepts, including Ampere’s law and the principles of inductance.
The Role of Electric Current
One fascinating fact about the Biot-Savart Law is that it revolves around the concept of electric current. The law states that the magnetic field produced at a specific point in space is directly proportional to the magnitude of the current flowing through the wire and inversely proportional to the square of the distance from the wire.
It Applies to Any Current-Carrying Wire
Another extraordinary aspect of the Biot-Savart Law is its universality. It is applicable to any configuration of current-carrying wires, whether straight or curved, infinite or finite in length. This versatility enables physicists and engineers to analyze intricate systems and gain insights into the behavior of magnetic fields.
The Magnetic Field Direction
The Biot-Savart Law reveals that the direction of the magnetic field produced by a current-carrying wire depends on the direction of the current. The field forms concentric circles around the wire, with the clockwise or counterclockwise orientation determined by the direction of the current flow.
The Superposition Principle
The Biot-Savart Law adheres to the principle of superposition, meaning that the total magnetic field at a specific point due to multiple current segments can be determined by summing the contributions from each segment individually. This principle allows for the analysis of complex systems with multiple currents.
Magnetic Field of a Solenoid
The Biot-Savart Law offers insights into the magnetic field produced by a current-carrying solenoid, which is essentially a tightly wound coil of wire. By applying the law, it is possible to calculate the field strength and direction inside and outside the solenoid, contributing to the understanding of electromagnetic devices like transformers and inductors.
Support for Ampere’s Circuital Law
The Biot-Savart Law provides the theoretical foundation for Ampere’s Circuital Law, which relates the magnetic field along a closed loop to the net current enclosed by the loop. By combining these two principles, scientists have been able to unravel the beautiful connection between currents, magnetic fields, and their interplay.
Integration for Complex Geometries
When dealing with complex geometries of current-carrying wires, the Biot-Savart Law can be elegant yet intricately challenging. By utilizing calculus and integration techniques, physicists and engineers can extend the application of the law to more intricate systems, such as curved wires and three-dimensional configurations.
Magnetic Field of a Straight Wire
A straight wire carrying current is a simple yet intriguing scenario to analyze using the Biot-Savart Law. The law reveals that the magnetic field around the wire exhibits a circular pattern perpendicular to the wire, with the field strength decreasing as the distance from the wire increases.
Continuous Current Distribution
The Biot-Savart Law can also be employed to analyze systems with continuous current distributions, such as a uniform current density flowing through a thin wire. This application demonstrates the law’s versatility in handling different scenarios and provides valuable insights into the magnetic field produced by such distributions.
Contributions to Inductance
Inductance, a key property in electrical circuits, relies on the principles governed by the Biot-Savart Law. Inductors, devices designed to store energy in the form of a magnetic field, utilize the law to determine the relationship between the current flowing through a wire coil and the induced magnetic flux.
Validity in Practical Applications
The Biot-Savart Law’s validity extends beyond theoretical physics, finding applications in various fields. Engineers rely on this law to analyze the behavior of magnetic fields in transformers, motors, generators, and many other electromagnetic devices that power our modern world.
In conclusion, the 12 extraordinary facts about the Biot-Savart Law shed light on its significance and practical applications in understanding the magnetic fields produced by current-carrying wires. From its foundational role in electromagnetism to its universal applicability and support for other laws and principles, the Biot-Savart Law continues to fascinate researchers, engineers, and physicists alike, unraveling the secrets of the magnetism that surrounds us.
Conclusion
The Biot-Savart Law is a fundamental principle in physics that describes the magnetic field generated by a current-carrying wire. Understanding this law is crucial for comprehending the behavior of magnetic fields and their effects on electric currents. In this article, we have explored 12 extraordinary facts about the Biot-Savart Law.We learned that the law was discovered by two prominent physicists, Biot and Savart, in the early 19th century. It states that the magnetic field at any point in space is directly proportional to the current flowing through a small segment of wire and inversely proportional to the distance from that segment.We also discovered that the Biot-Savart Law is applicable to any shape of current-carrying wire, making it a versatile tool for calculating magnetic fields. Moreover, it serves as the foundation for understanding complex electromagnetic phenomena, such as Ampere’s Law and the concept of magnetic flux.In conclusion, the Biot-Savart Law is a fundamental concept that allows us to analyze and predict the behavior of magnetic fields generated by electric currents. Its applications span various areas of physics and engineering, making it a crucial principle to grasp for anyone interested in the world of electromagnetism.
FAQs
1. What is the Biot-Savart Law?
The Biot-Savart Law is a fundamental principle in physics that describes the magnetic field generated by a current-carrying wire.
2. Who discovered the Biot-Savart Law?
The law was discovered by two prominent physicists, Biot and Savart, in the early 19th century.
3. What does the Biot-Savart Law state?
The law states that the magnetic field at any point in space is directly proportional to the current flowing through a small segment of wire and inversely proportional to the distance from that segment.
4. Is the Biot-Savart Law applicable to all shapes of current-carrying wires?
Yes, the law is applicable to any shape of current-carrying wire, making it a versatile tool for calculating magnetic fields.
5. What are some applications of the Biot-Savart Law?
The Biot-Savart Law serves as the foundation for understanding complex electromagnetic phenomena, such as Ampere’s Law and the concept of magnetic flux. It is widely used in various areas of physics and engineering.
6. Why is it important to understand the Biot-Savart Law?
Understanding the Biot-Savart Law is crucial for comprehending the behavior of magnetic fields and their effects on electric currents. It allows for the analysis and prediction of magnetic field behavior in various physical systems.
Biot-Savart Law's extraordinary facts captivate physics enthusiasts, but there's more to explore! Unravel enigmatic aspects of this magnetic field law, mind-blowing magnetostatics revelations await. Satisfy your curiosity - keep reading to expand your knowledge!
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.


