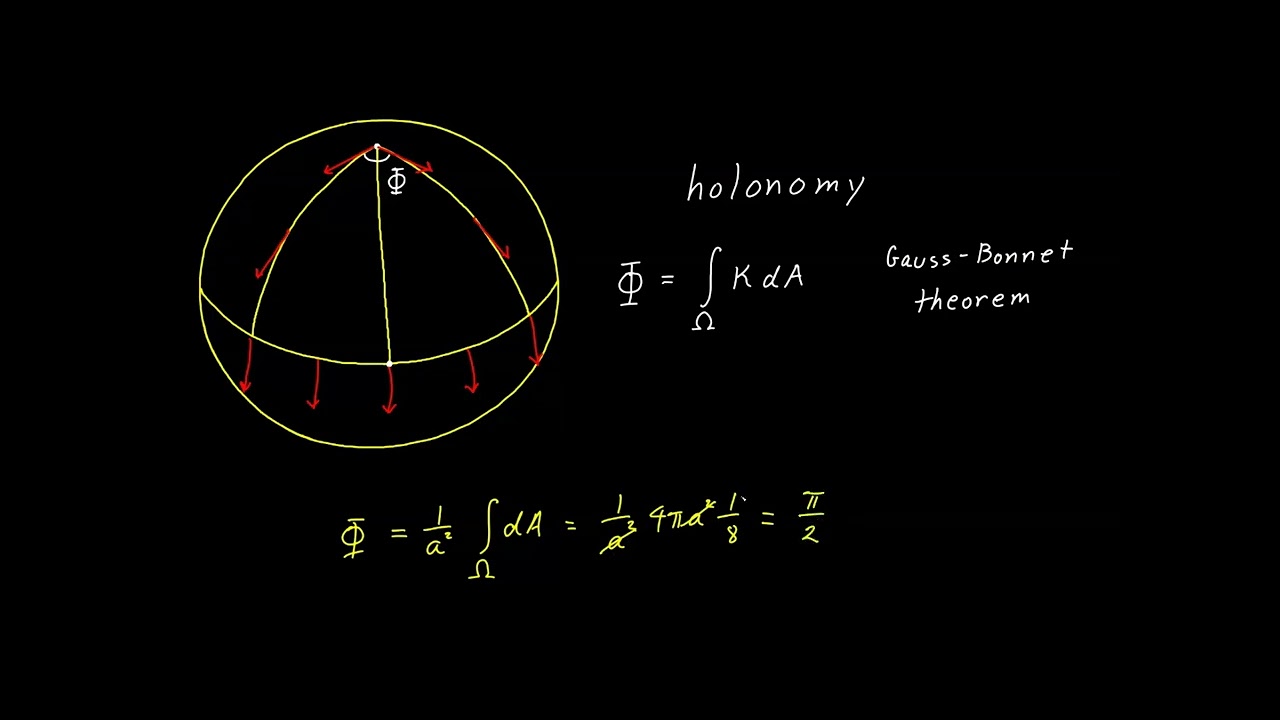
Holonomy might sound like a complex term, but it's a fascinating concept in mathematics and physics. Holonomy refers to how much a vector changes when it is parallel transported around a closed loop in a curved space. Imagine walking around a mountain with a compass; when you return to your starting point, the compass needle might point in a different direction. This change is what holonomy measures. It's crucial in understanding the geometry of spaces, especially in general relativity and gauge theory. Ready to dive into 40 intriguing facts about holonomy? Let's get started!
What is Holonomy?
Holonomy is a concept from differential geometry that deals with how vectors change as they are parallel transported around a loop. It has applications in physics, especially in the theory of general relativity and gauge theory. Here are some fascinating facts about holonomy.
-
Holonomy comes from the Greek words "holos" (whole) and "nomos" (law), meaning it deals with the laws governing whole loops.
-
Parallel transport is the process of moving a vector along a curve while keeping it parallel to itself according to a given connection.
-
Connections in differential geometry provide a way to differentiate vector fields along curves on a manifold.
-
Manifolds are mathematical spaces that locally resemble Euclidean space and are the primary objects of study in differential geometry.
-
Holonomy group is the group of all transformations obtained by parallel transporting vectors around all possible loops based at a point.
Holonomy in Physics
Holonomy isn't just a mathematical curiosity; it has real-world applications, especially in physics.
-
General relativity uses holonomy to describe how spacetime curvature affects the motion of particles and light.
-
Gauge theory applies holonomy to describe how fields like the electromagnetic field change as particles move through space.
-
Yang-Mills theory, a cornerstone of particle physics, relies on holonomy to understand the behavior of fundamental particles.
-
Fiber bundles are used in physics to describe fields and forces, with holonomy playing a key role in their structure.
-
Aharonov-Bohm effect demonstrates how holonomy can affect quantum particles, showing that electromagnetic potentials have physical significance.
Mathematical Properties of Holonomy
Holonomy has rich mathematical properties that make it a fascinating subject of study.
-
Ambrose-Singer theorem relates the holonomy group of a connection to its curvature.
-
Curvature measures how much a geometric object deviates from being flat, and it directly influences holonomy.
-
Riemannian manifolds are manifolds equipped with a way to measure distances and angles, and their holonomy groups provide important geometric information.
-
Symmetric spaces have holonomy groups that are often simpler to study, making them important in geometry and physics.
-
Holonomy reduction occurs when the holonomy group of a manifold is a proper subgroup of the general linear group, leading to special geometric structures.
Special Holonomy Groups
Certain holonomy groups are particularly important in both mathematics and physics.
-
SU(2) and SU(3) are special unitary groups that appear in the study of holonomy in quantum field theory.
-
Spin(7) is a special holonomy group that appears in the study of 8-dimensional manifolds with exceptional geometric structures.
-
G2 is another exceptional holonomy group, important in the study of 7-dimensional manifolds.
-
Calabi-Yau manifolds have holonomy groups that are special unitary groups, making them important in string theory.
-
Kähler manifolds have holonomy groups that are unitary groups, leading to rich geometric and physical properties.
Holonomy and Topology
Holonomy also has deep connections with topology, the study of the properties of space that are preserved under continuous deformations.
-
Fundamental group of a manifold is related to its holonomy group, providing insights into the manifold's topological structure.
-
Covering spaces can simplify the study of holonomy by lifting loops to simpler spaces.
-
Flat connections have trivial holonomy, meaning parallel transport around any loop returns the vector to its original position.
-
Holonomy and homotopy are related, as homotopy classes of loops can influence the holonomy group.
-
Chern-Simons theory uses holonomy to study 3-dimensional manifolds and their topological properties.
Applications of Holonomy
Holonomy has a wide range of applications beyond pure mathematics and theoretical physics.
-
Robotics uses holonomy to understand the motion of robots and their ability to navigate complex environments.
-
Computer graphics applies holonomy to simulate realistic motion and deformation of objects.
-
Control theory uses holonomy to design systems that can follow desired paths and trajectories.
-
Cryptography can use holonomy to create secure communication protocols based on geometric properties.
-
Mechanical engineering applies holonomy to design systems with precise motion control, such as robotic arms and CNC machines.
Holonomy in Higher Dimensions
Holonomy becomes even more interesting in higher-dimensional spaces, leading to new mathematical and physical phenomena.
-
Higher-dimensional manifolds have more complex holonomy groups, leading to richer geometric structures.
-
String theory uses holonomy in higher dimensions to describe the behavior of fundamental particles and forces.
-
M-theory extends string theory to 11 dimensions, with holonomy playing a key role in its mathematical structure.
-
Mirror symmetry in string theory relates holonomy groups of different manifolds, leading to deep mathematical insights.
-
Special holonomy in higher dimensions can lead to new types of geometric structures, such as G2 and Spin(7) manifolds.
Holonomy and Quantum Mechanics
Holonomy also has important implications for quantum mechanics and the behavior of quantum systems.
-
Berry phase is a quantum mechanical phenomenon where holonomy affects the phase of a particle's wavefunction.
-
Quantum holonomy describes how quantum states change as they are transported around loops in parameter space.
-
Topological quantum computing uses holonomy to create robust quantum bits that are resistant to errors.
-
Quantum field theory applies holonomy to understand the behavior of fields and particles in curved spacetime.
-
Quantum gravity theories, such as loop quantum gravity, use holonomy to describe the quantum properties of spacetime itself.
Holonomy: A Fascinating Concept
Holonomy, a concept from differential geometry, offers a unique way to understand the curvature of space. It’s all about how vectors change as they move around a loop. This idea has applications in physics, particularly in general relativity and gauge theory. By studying holonomy, scientists can gain insights into the fundamental nature of the universe.
Understanding holonomy isn’t just for mathematicians and physicists. It’s a concept that can spark curiosity and wonder in anyone interested in the mysteries of space and time. Whether you’re a student, a teacher, or just someone who loves learning new things, holonomy has something to offer.
So next time you think about the universe, remember holonomy. It’s a small but powerful piece of the puzzle that helps us understand the world around us. Keep exploring, keep questioning, and keep learning.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
