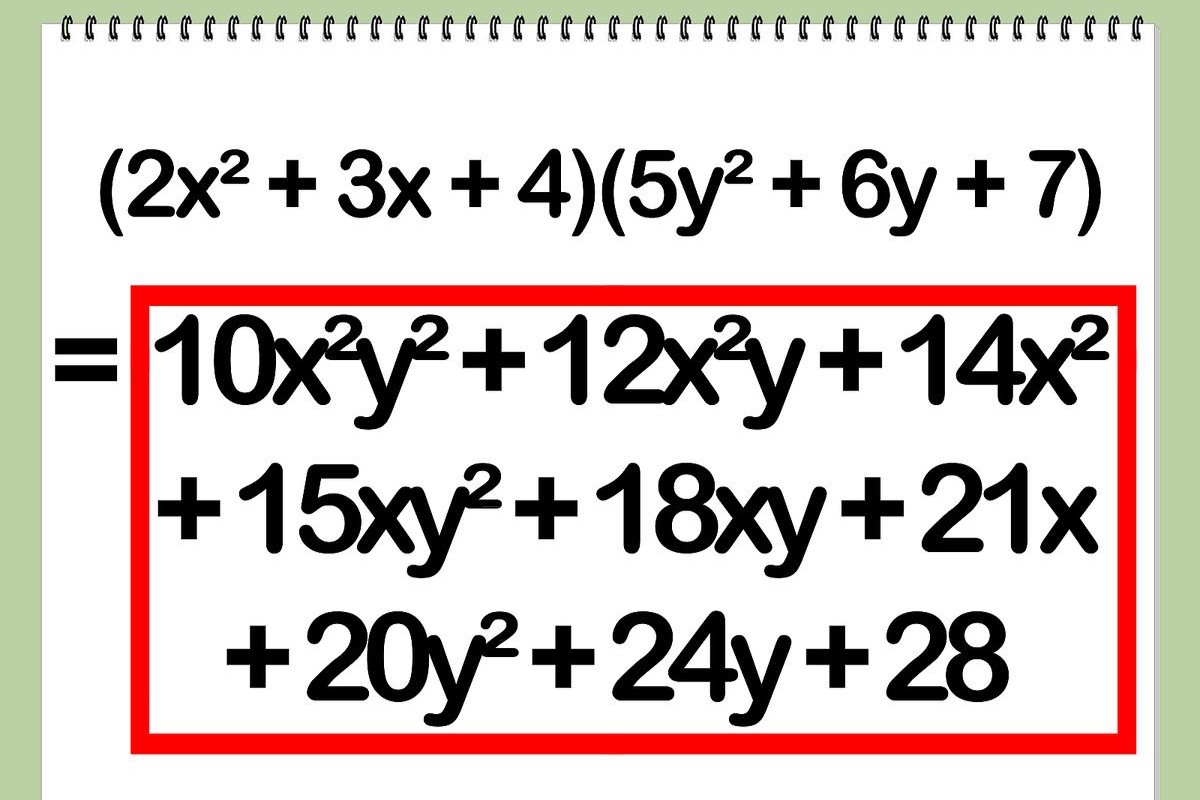
Polynomials are everywhere in math, from simple algebra to advanced calculus. But what exactly are they? Polynomials are expressions made up of variables and coefficients, involving operations like addition, subtraction, and multiplication. They can be as simple as (x + 2) or as complex as (4x^3 – 3x^2 + 2x – 1). These mathematical expressions are fundamental in solving equations, modeling real-world scenarios, and even in computer algorithms. Curious about how they work or why they matter? Here are 39 intriguing facts about polynomials that will help you understand their importance and versatility. Whether you're a student, a teacher, or just a math enthusiast, these facts will give you a deeper appreciation for these powerful mathematical tools.
What Are Polynomials?
Polynomials are mathematical expressions involving variables and coefficients. They are used in various fields like physics, engineering, and economics. Let's dive into some fascinating facts about polynomials.
-
Polynomials can have one or more terms. Each term includes a variable raised to a power and a coefficient.
-
The degree of a polynomial is the highest power of the variable in the expression. For example, in (3x^4 + 2x^3 – x + 7), the degree is 4.
-
Polynomials can be classified based on their degree. A polynomial of degree 1 is called linear, degree 2 is quadratic, degree 3 is cubic, and so on.
-
The term "polynomial" comes from the Greek words "poly," meaning many, and "nomial," meaning terms.
-
A polynomial with only one term is called a monomial. Examples include (5x) and (7y^3).
-
A polynomial with two terms is called a binomial. Examples include (x + 1) and (3x^2 – 4).
-
A polynomial with three terms is called a trinomial. Examples include (x^2 + 2x + 1) and (4y^3 – y + 5).
-
Polynomials are closed under addition, subtraction, and multiplication. This means adding, subtracting, or multiplying two polynomials results in another polynomial.
-
Polynomials are not closed under division. Dividing two polynomials can result in a rational function, which is not always a polynomial.
-
The coefficients in a polynomial can be any real number, including zero.
Applications of Polynomials
Polynomials are not just abstract mathematical concepts. They have practical applications in various fields.
-
In physics, polynomials are used to describe the motion of objects. For example, the equation of motion for a freely falling object is a quadratic polynomial.
-
In economics, polynomials can model cost functions and revenue functions, helping businesses maximize profit.
-
In engineering, polynomials are used in control systems to design stable and efficient systems.
-
Polynomials are used in computer graphics to draw curves and surfaces. Bezier curves, which are used in graphic design, are defined by polynomials.
-
In statistics, polynomial regression is used to model the relationship between variables.
-
Polynomials are used in coding theory to detect and correct errors in data transmission.
-
In chemistry, polynomials can describe the relationship between the concentration of reactants and the rate of reaction.
-
Polynomials are used in cryptography to create secure communication systems.
-
In biology, polynomials can model population growth and the spread of diseases.
-
Polynomials are used in finance to model the growth of investments and the behavior of stock prices.
Interesting Properties of Polynomials
Polynomials have some unique properties that make them interesting to study.
-
The Fundamental Theorem of Algebra states that every non-zero polynomial has at least one complex root.
-
A polynomial equation of degree (n) has exactly (n) roots, counting multiplicities.
-
The roots of a polynomial are the values of the variable that make the polynomial equal to zero.
-
Polynomials can be factored into linear factors if all their roots are known.
-
The Remainder Theorem states that the remainder of the division of a polynomial by a linear polynomial (x – a) is equal to the value of the polynomial at (a).
-
The Factor Theorem states that (x – a) is a factor of a polynomial if and only if the polynomial evaluates to zero at (a).
-
Polynomials can be differentiated and integrated like other functions. The derivative of a polynomial is another polynomial.
-
The graph of a polynomial function is a smooth, continuous curve.
-
Polynomials are used to approximate more complex functions. Taylor and Maclaurin series are examples of polynomial approximations.
-
The coefficients of a polynomial can be determined if its roots are known, using Vieta's formulas.
Famous Polynomials
Some polynomials have special names and properties that make them famous in mathematics.
-
The quadratic polynomial (ax^2 + bx + c) is one of the most studied polynomials. Its roots can be found using the quadratic formula.
-
The cubic polynomial (ax^3 + bx^2 + cx + d) has a more complex formula for its roots, discovered by mathematicians in the 16th century.
-
The quartic polynomial (ax^4 + bx^3 + cx^2 + dx + e) also has a formula for its roots, but it is even more complicated than the cubic formula.
-
The polynomial (x^n – 1) is called a cyclotomic polynomial. Its roots are the (n)th roots of unity.
-
Chebyshev polynomials are used in approximation theory and numerical analysis. They have special properties that make them useful for minimizing errors.
-
Legendre polynomials are used in physics, particularly in solving problems involving spherical coordinates.
-
Hermite polynomials are used in probability theory and combinatorics.
-
Laguerre polynomials are used in quantum mechanics, particularly in the study of the hydrogen atom.
-
Bernoulli polynomials are used in number theory and the study of special functions.
The Power of Polynomials
Polynomials are more than just a bunch of numbers and variables. They’re the backbone of algebra, helping us solve equations, model real-world situations, and understand complex concepts in math and science. From simple linear equations to intricate polynomial functions, these expressions play a crucial role in various fields like engineering, physics, and economics.
Understanding polynomials can boost your problem-solving skills and open doors to advanced mathematical studies. They’re not just academic exercises; they’re tools that can help you make sense of the world around you. Whether you’re calculating the trajectory of a rocket or figuring out the best deal at the grocery store, polynomials are there, working behind the scenes.
So next time you encounter a polynomial, remember its importance and the many ways it impacts our daily lives. Keep exploring, keep learning, and let the power of polynomials guide you.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
