39 Facts About Goldbach

39 Facts about Goldbach's Conjecture

Goldbach's Conjecture is one of the oldest unsolved problems in number theory. It has fascinated mathematicians for centuries. Let's dive into some intriguing facts about this mathematical mystery.

The Origin of Goldbach's Conjecture

Goldbach's Conjecture has a rich history that dates back to the 18th century. Here are some key points about its origin.

1. 01

   Goldbach's Letter: In 1742, Christian Goldbach wrote a letter to Leonhard Euler, proposing that every even number greater than 2 can be expressed as the sum of two prime numbers.

2. 02

   Euler's Interest: Euler, one of the greatest mathematicians of all time, took a keen interest in Goldbach's conjecture and included it in his correspondence with other mathematicians.

3. 03

   Original Formulation: Goldbach's original statement was slightly different. He suggested that every integer greater than 2 can be written as the sum of three primes. Euler reformulated it to the version we know today.

4. 04

   Historical Context: The conjecture emerged during a period of intense mathematical exploration and discovery in Europe.

Mathematical Significance

Goldbach's Conjecture holds a special place in the world of mathematics due to its simplicity and the challenge it presents.

5. 05

   Simple Statement: Despite its simple formulation, proving the conjecture has proven to be extremely difficult.

6. 06

   Prime Numbers: The conjecture highlights the unique properties of prime numbers, which are the building blocks of number theory.

7. 07

   Unsolved Problem: It remains one of the oldest unsolved problems in mathematics, attracting the attention of both amateur and professional mathematicians.

8. 08

   Computational Efforts: Modern computers have verified the conjecture for even numbers up to very large limits, but a general proof remains elusive.

Attempts to Prove the Conjecture

Over the years, many mathematicians have tried to prove Goldbach's Conjecture. Here are some notable efforts.

9. 09

   Hardy and Littlewood: In the early 20th century, G.H. Hardy and J.E. Littlewood made significant progress using analytical methods.

10. 10

    Vinogradov's Theorem: In 1937, Ivan Vinogradov proved that every sufficiently large odd number can be expressed as the sum of three primes, which is related to Goldbach's original statement.

11. 11

    Computer Verification: Extensive computational efforts have verified the conjecture for even numbers up to 4 x 10^18.

12. 12

    Terence Tao: In 2013, Terence Tao made progress by showing that every odd number greater than 1 can be expressed as the sum of at most five primes.

Interesting Properties

Goldbach's Conjecture has some fascinating properties and implications.

13. 13

    Symmetry: The conjecture implies a certain symmetry in the distribution of prime numbers.

14. 14

    Prime Pairs: It suggests that prime pairs exist for every even number, which has implications for the study of prime gaps.

15. 15

    Additive Number Theory: The conjecture is a central problem in additive number theory, which studies the properties of numbers under addition.

16. 16

    Related Conjectures: It has inspired other conjectures, such as the Twin Prime Conjecture and the Polignac's Conjecture.

Computational Advances

Advancements in computing have played a crucial role in exploring Goldbach's Conjecture.

17. 17

    Supercomputers: Supercomputers have been used to verify the conjecture for very large even numbers.

18. 18

    Distributed Computing: Projects like the Great Internet Mersenne Prime Search (GIMPS) have utilized distributed computing to test the conjecture.

19. 19

    Algorithm Development: New algorithms have been developed to efficiently test large numbers for primality and verify the conjecture.

20. 20

    Record-Breaking Verifications: The largest even number verified to satisfy the conjecture is currently 4 x 10^18.

Cultural Impact

Goldbach's Conjecture has also made its way into popular culture and inspired various works.

21. 21

    Books: It has been featured in several books on mathematics and number theory.

22. 22

    Documentaries: Documentaries and TV shows have explored the mystery and history of the conjecture.

23. 23

    Mathematical Art: Artists have created works inspired by the beauty and complexity of the conjecture.

24. 24

    Educational Material: It is often included in educational material to introduce students to the wonders of number theory.

Modern Research

Research on Goldbach's Conjecture continues to this day, with mathematicians exploring new approaches and techniques.

25. 25

    Analytical Methods: Researchers are developing new analytical methods to tackle the conjecture.

26. 26

    Probabilistic Approaches: Some mathematicians are using probabilistic approaches to gain insights into the distribution of prime numbers.

27. 27

    Collaborative Efforts: International collaborations are bringing together mathematicians from around the world to work on the problem.

28. 28

    Workshops and Conferences: Workshops and conferences dedicated to number theory often feature discussions on Goldbach's Conjecture.

Fun Facts

Here are some fun and quirky facts about Goldbach's Conjecture.

29. 29

    Goldbach's Prime: A prime number that can be paired with another prime to form an even number is sometimes called a "Goldbach prime."

30. 30

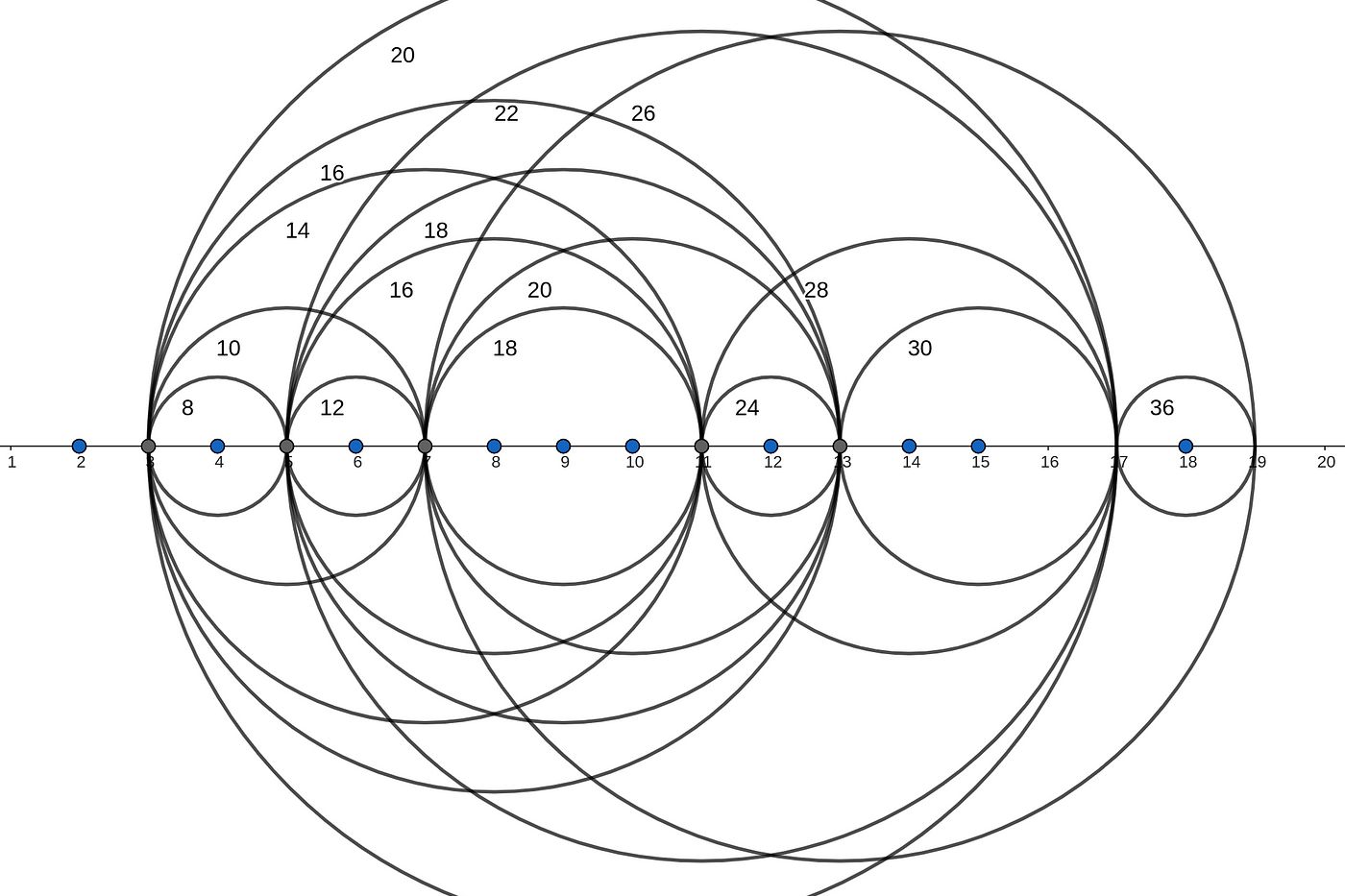
    Goldbach Partitions: The different ways an even number can be expressed as the sum of two primes are called "Goldbach partitions."

31. 31

    Mathematical Puzzles: The conjecture has inspired numerous mathematical puzzles and challenges.

32. 32

    Amateur Mathematicians: Many amateur mathematicians have contributed to the study of the conjecture.

Challenges and Controversies

Goldbach's Conjecture has faced its share of challenges and controversies over the years.

33. 33

    False Proofs: Numerous false proofs have been proposed, only to be later debunked.

34. 34

    Mathematical Rigor: Ensuring mathematical rigor in proofs is a significant challenge in tackling the conjecture.

35. 35

    Publication Issues: Some researchers have faced difficulties in getting their work on the conjecture published.

36. 36

    Skepticism: There is some skepticism in the mathematical community about whether a proof will ever be found.

Future Prospects

What does the future hold for Goldbach's Conjecture? Here are some possibilities.

37. 37

    Breakthroughs: A breakthrough in number theory could potentially lead to a proof of the conjecture.

38. 38

    New Techniques: Advances in mathematical techniques and computational power may bring us closer to a solution.

39. 39

    Continued Fascination: Regardless of whether it is ever proven, Goldbach's Conjecture will continue to fascinate and inspire mathematicians for generations to come.

The Enigma of Goldbach's Conjecture

Goldbach's Conjecture remains one of mathematics' most intriguing puzzles. Despite centuries of effort, no one has definitively proven or disproven it. This simple yet profound statement about prime numbers has captivated mathematicians and enthusiasts alike. Its allure lies in its elegance and the challenge it presents.

Understanding the conjecture's history and the efforts to solve it gives us a glimpse into the world of mathematical discovery. From Euler's early work to modern computational attempts, each step brings us closer to unraveling this mystery.

Whether you're a math whiz or just curious, Goldbach's Conjecture offers a fascinating journey into the heart of number theory. Who knows? Maybe one day, someone will crack the code, and we'll finally have an answer to this age-old question. Until then, the quest continues, inspiring new generations of thinkers.