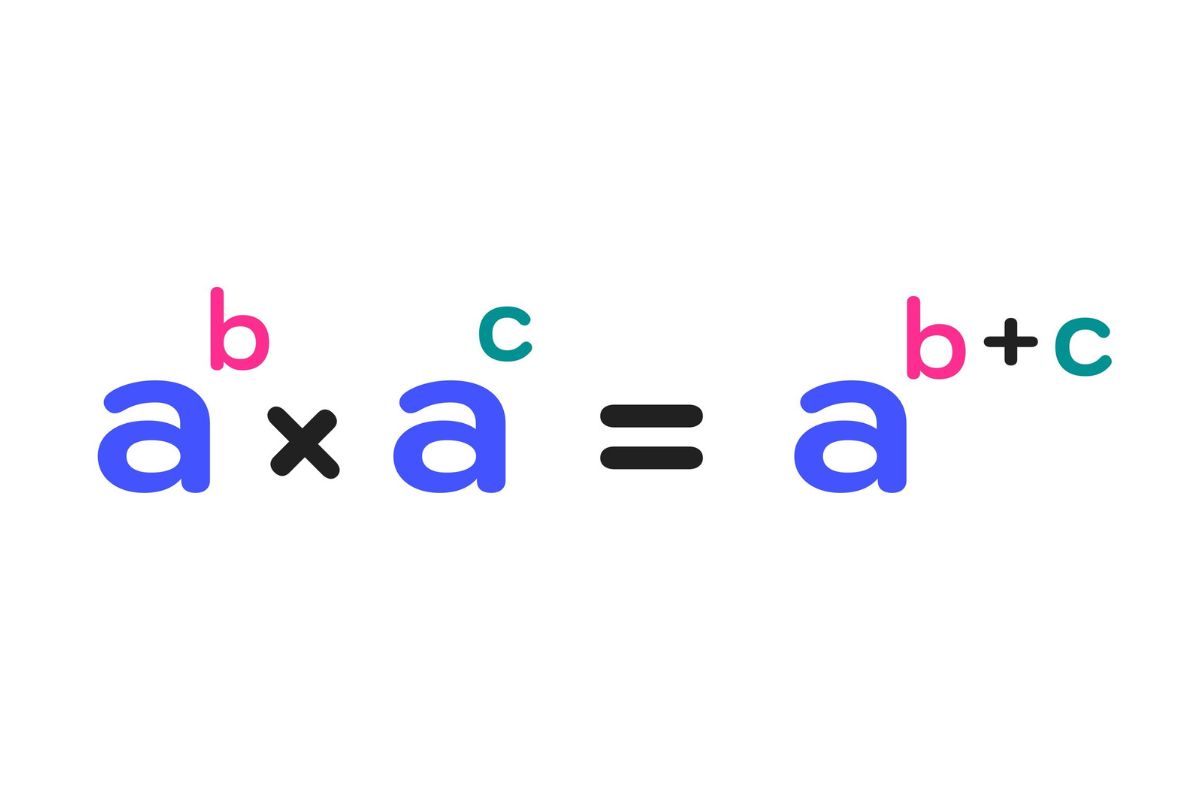
Exponents might seem tricky at first, but they’re just a way to show repeated multiplication. For example, (2^3) means (2 \times 2 \times 2). Why are exponents important? They help simplify large numbers and make calculations easier. Imagine trying to write out (10^{10}) without exponents! They also play a big role in science, engineering, and computer science. Did you know that exponents can be negative or even fractions? Negative exponents represent division, while fractional exponents relate to roots. Understanding exponents can unlock new math skills and make complex problems simpler. Ready to learn some cool facts about exponents? Let’s dive in!
What Are Exponents?
Exponents are a way to express repeated multiplication of the same number. They are used in various fields, from mathematics to computer science. Here are some fascinating facts about exponents.
-
Exponents are also called powers. When you see a number like 2^3, it means 2 is raised to the power of 3.
-
The base is the number being multiplied. In 2^3, 2 is the base.
-
The exponent tells how many times to multiply the base. In 2^3, the exponent is 3, meaning 2 * 2 * 2.
-
Any number to the power of 1 is itself. For example, 5^1 equals 5.
-
Any number to the power of 0 is 1. This rule applies to all numbers except zero itself.
-
Negative exponents represent division. For instance, 2^-3 equals 1/(2^3) or 1/8.
Exponents in Real Life
Exponents aren't just for math class. They have practical applications in everyday life and various scientific fields.
-
Exponential growth describes rapid increase. This concept is used in population studies and finance.
-
Exponential decay describes rapid decrease. It's often used in radioactive decay and depreciation of assets.
-
Compound interest uses exponents. The formula for compound interest involves raising the base to the power of the number of periods.
-
Computer algorithms use exponents. Many algorithms, especially those involving data encryption, rely on exponents.
-
Scientific notation uses exponents. This notation helps express very large or very small numbers, like the distance between stars.
Mathematical Properties of Exponents
Understanding the properties of exponents can make solving problems easier. Here are some key properties.
-
Product of powers property. When multiplying like bases, add the exponents: a^m * a^n = a^(m+n).
-
Quotient of powers property. When dividing like bases, subtract the exponents: a^m / a^n = a^(m-n).
-
Power of a power property. When raising a power to another power, multiply the exponents: (a^m)^n = a^(m*n).
-
Power of a product property. Distribute the exponent to each factor: (ab)^n = a^n * b^n.
-
Power of a quotient property. Distribute the exponent to both the numerator and the denominator: (a/b)^n = a^n / b^n.
Fun Facts About Exponents
Exponents can be fun and surprising. Here are some interesting tidbits.
-
Exponents can be fractions. A fractional exponent like 2^(1/2) is the same as the square root of 2.
-
Exponents can be irrational numbers. For example, e^π is an irrational number.
-
Exponents can be complex numbers. Complex exponents involve imaginary numbers, like i, where i^2 = -1.
-
Exponents are used in fractals. Fractals are complex patterns that repeat at different scales, often described using exponents.
-
Exponents are used in logarithms. Logarithms are the inverse of exponents, helping solve equations involving exponents.
Historical Facts About Exponents
Exponents have a rich history, dating back to ancient times. Here are some historical facts.
-
The concept of exponents dates back to ancient India. Mathematicians like Aryabhata used them in their work.
-
Rene Descartes popularized exponents in Europe. He introduced the notation we use today in the 17th century.
-
Isaac Newton used exponents in calculus. His work on calculus involved extensive use of exponents.
-
Leonhard Euler expanded the use of exponents. Euler's work in the 18th century included many applications of exponents.
Exponents in Technology
Exponents play a crucial role in modern technology. Here are some ways they are used.
-
Exponents are used in computer graphics. They help create realistic images and animations.
-
Exponents are used in data encryption. Many encryption algorithms rely on the properties of exponents.
-
Exponents are used in machine learning. Algorithms that power AI often involve exponents.
-
Exponents are used in signal processing. They help analyze and manipulate signals in telecommunications.
Exponents in Nature
Exponents can be found in natural phenomena. Here are some examples.
-
Exponential growth in bacteria. Bacteria can multiply rapidly, showing exponential growth.
-
Exponential decay in radioactive materials. Radioactive substances decay at an exponential rate.
-
Fractals in nature. Many natural patterns, like snowflakes and coastlines, can be described using exponents.
The Power of Exponents
Exponents play a huge role in math and science. They simplify complex calculations, making it easier to handle large numbers. From calculating compound interest to understanding scientific notation, exponents are everywhere. Knowing how to use them can make a big difference in solving problems quickly and accurately.
Understanding exponents also helps in fields like computer science, physics, and engineering. They’re not just for math class; they’re tools for real-world applications. Whether you’re coding, designing circuits, or studying the universe, exponents are essential.
So, next time you see a tiny number floating above another, remember it’s not just a number. It’s a powerful tool that can unlock a world of possibilities. Keep practicing, and you’ll find that exponents are not as intimidating as they seem. They’re just another way to make math work for you.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
