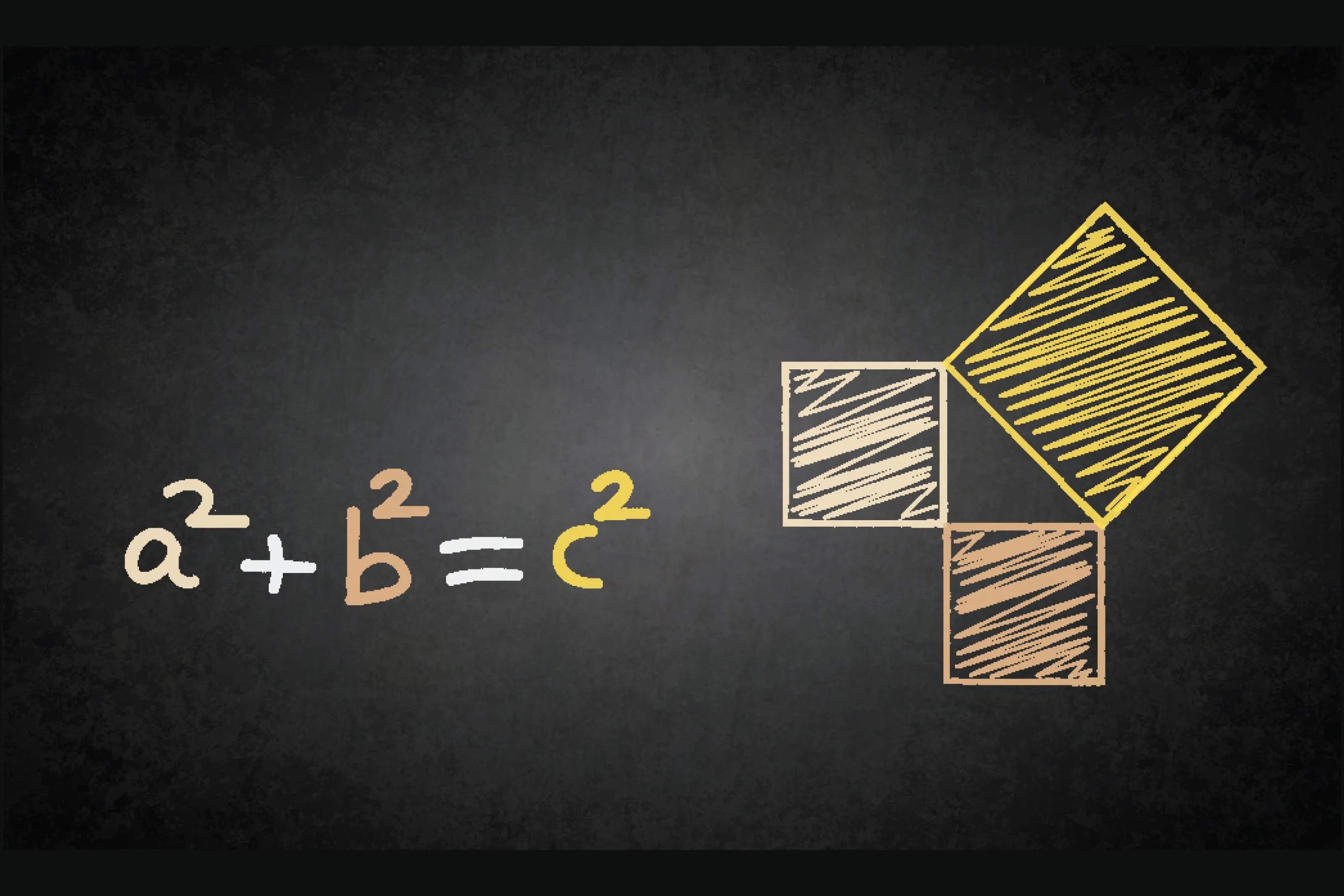
What is a theorem? A theorem is a statement or proposition that has been proven to be true through a logical sequence of reasoning. In mathematics, theorems are the backbone of understanding complex concepts and solving intricate problems. They often start as conjectures—ideas that seem true but need proof. Once proven, they become the building blocks for further discoveries. Think of the Pythagorean Theorem, which helps us understand the relationship between the sides of a right triangle. Theorems aren't just limited to math; they can be found in physics, computer science, and even philosophy. Understanding theorems can open up a world of knowledge and problem-solving skills.
What is a Theorem?
A theorem is a statement that has been proven to be true based on previously established statements, such as other theorems, axioms, and postulates. Theorems are fundamental in mathematics and logic, providing a foundation for further study and application.
- Theorem comes from the Greek word "theorema," meaning "speculation" or "looking at."
- A theorem must be proven through a logical sequence of statements, starting from axioms and previously proven theorems.
- The Pythagorean Theorem is one of the most famous theorems, stating that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Famous Theorems in History
Throughout history, many theorems have shaped the course of mathematics and science. Here are some of the most notable ones:
- Euclid's Elements contains many important theorems, including the proof that there are infinitely many prime numbers.
- Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation (a^n + b^n = c^n) for any integer value of n greater than 2. It was proven by Andrew Wiles in 1994.
- Gödel's Incompleteness Theorems show that in any consistent formal system, there are statements that are true but cannot be proven within the system.
- The Fundamental Theorem of Calculus links the concept of the derivative of a function with the concept of the integral.
Theorems in Geometry
Geometry is rich with theorems that help us understand shapes, sizes, and the properties of space.
- Thales' Theorem states that if A, B, and C are points on a circle where the line segment AC is a diameter, then the angle ABC is a right angle.
- Pascal's Theorem involves a hexagon inscribed in a conic section, stating that the points of intersection of opposite sides lie on a straight line.
- Ceva's Theorem provides a criterion for three cevians (lines from the vertices of a triangle to the opposite sides) to be concurrent.
Theorems in Algebra
Algebraic theorems help us solve equations and understand the relationships between numbers.
- The Fundamental Theorem of Algebra states that every non-constant polynomial equation has at least one complex root.
- Vieta's Formulas relate the coefficients of a polynomial to sums and products of its roots.
- The Binomial Theorem describes the algebraic expansion of powers of a binomial.
Theorems in Number Theory
Number theory explores the properties and relationships of numbers, especially integers.
- The Prime Number Theorem describes the asymptotic distribution of prime numbers among positive integers.
- Wilson's Theorem states that a natural number n > 1 is a prime number if and only if ((n-1)! + 1) is divisible by n.
- Lagrange's Four Square Theorem states that every natural number can be represented as the sum of four integer squares.
Theorems in Calculus
Calculus theorems are essential for understanding change and motion.
- Taylor's Theorem provides an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
- Stokes' Theorem generalizes several theorems from vector calculus, relating surface integrals of vector fields to line integrals.
- Green's Theorem relates the double integral over a plane region to a line integral around its boundary.
Theorems in Probability and Statistics
Probability and statistics use theorems to predict outcomes and analyze data.
- Bayes' Theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event.
- The Central Limit Theorem states that the distribution of the sum (or average) of a large number of independent, identically distributed variables approaches a normal distribution.
- The Law of Large Numbers states that as a sample size grows, its mean gets closer to the average of the whole population.
Theorems in Computer Science
Computer science also relies on theorems to understand algorithms and computational limits.
- The Halting Theorem states that there is no general algorithm that can determine whether any given program will finish running or continue to run forever.
- The Cook-Levin Theorem proves that the Boolean satisfiability problem (SAT) is NP-complete.
- Kleene's Theorem provides a characterization of regular languages in terms of regular expressions and finite automata.
Miscellaneous Theorems
Some theorems don't fit neatly into one category but are still incredibly important.
- Arrow's Impossibility Theorem states that no rank-order voting system can be designed that always satisfies a set of fairness criteria.
- The Noether Theorem links symmetries and conservation laws in physics.
- The Banach-Tarski Paradox states that a solid ball can be split into a finite number of pieces, which can then be reassembled into two solid balls identical to the original.
Theorems in Modern Mathematics
Modern mathematics continues to evolve, with new theorems being proven regularly.
- The Poincaré Conjecture, proven by Grigori Perelman in 2003, states that every simply connected, closed 3-manifold is homeomorphic to a 3-sphere.
Final Thoughts on Theorems
Theorems are the backbone of mathematics. They provide a solid foundation for understanding complex concepts. From Pythagoras' theorem to Fermat's Last Theorem, these mathematical statements have shaped the way we see the world. They aren't just abstract ideas; they have practical applications in engineering, physics, and even computer science. Knowing these facts can deepen your appreciation for the subject. Whether you're a student, a teacher, or just a curious mind, understanding theorems can open up new avenues of thought. So next time you encounter a theorem, remember its significance and the centuries of thought that went into proving it. Keep exploring, keep questioning, and who knows? You might just stumble upon a new theorem yourself.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
