What are Jacobians? Jacobians are mathematical tools used in calculus to describe how functions change when their input variables change. They are especially useful in multivariable calculus and vector calculus. Why are Jacobians important? They help in understanding transformations between different coordinate systems, which is crucial in fields like physics, engineering, and computer graphics. How do Jacobians work? By using partial derivatives, Jacobians form a matrix that represents the rate of change of each function with respect to each variable. This matrix, known as the Jacobian matrix, can be used to analyze and solve complex problems involving multiple variables. Want to learn more? Keep reading to uncover 26 fascinating facts about Jacobians that will deepen your understanding of this essential mathematical concept.
What is a Jacobian?
The Jacobian is a matrix of all first-order partial derivatives of a vector-valued function. It plays a crucial role in various fields, including mathematics, physics, and engineering. Here are some fascinating facts about Jacobians.
-
Named After Mathematician Carl Gustav Jacob Jacobi
The Jacobian matrix is named after Carl Gustav Jacob Jacobi, a German mathematician who made significant contributions to the theory of determinants and matrix algebra. -
Used in Multivariable Calculus
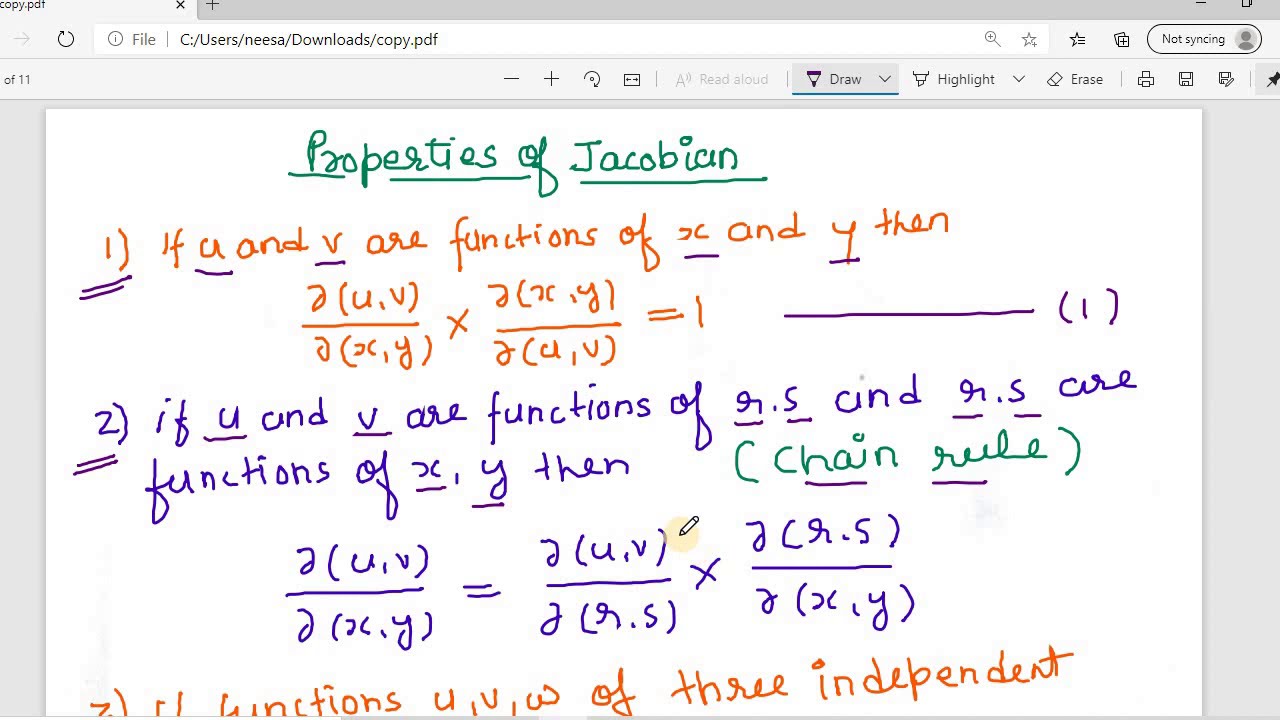
Jacobians are essential in multivariable calculus for transforming coordinates and changing variables in multiple integrals. -
Jacobian Determinant
The determinant of the Jacobian matrix, known as the Jacobian determinant, helps determine whether a transformation is invertible and measures how much a function stretches or shrinks volumes.
Applications in Physics
Jacobians are not just theoretical constructs; they have practical applications in physics. Here are some examples.
-
Fluid Dynamics
In fluid dynamics, Jacobians help describe the flow of fluids by relating different coordinate systems. -
Electromagnetism
Jacobians are used in electromagnetism to transform fields between different coordinate systems, such as Cartesian to spherical coordinates. -
General Relativity
In general relativity, Jacobians help describe how spacetime coordinates change under different reference frames.
Importance in Engineering
Engineers also rely on Jacobians for various applications, from robotics to structural analysis.
-
Robotics
In robotics, Jacobians are used to relate joint velocities to end-effector velocities, crucial for controlling robotic arms. -
Structural Analysis
Engineers use Jacobians in structural analysis to understand how forces and displacements transform under different conditions. -
Control Systems
Jacobians help design control systems by linearizing nonlinear systems around operating points.
Role in Computer Graphics
Jacobians have a significant role in computer graphics, particularly in rendering and animation.
-
Texture Mapping
Jacobians are used in texture mapping to transform textures accurately onto 3D models. -
Animation
In animation, Jacobians help simulate realistic movements by transforming joint angles to end-effector positions. -
Ray Tracing
Jacobians assist in ray tracing algorithms to calculate how light interacts with surfaces in a 3D environment.
Mathematical Properties
Jacobians have several interesting mathematical properties that make them useful in various calculations.
-
Chain Rule
The Jacobian matrix plays a crucial role in the multivariable chain rule, allowing the composition of functions to be differentiated easily. -
Inverse Function Theorem
The inverse function theorem uses the Jacobian determinant to determine if a function has a locally invertible function. -
Implicit Function Theorem
The implicit function theorem relies on the Jacobian matrix to solve equations involving multiple variables.
Jacobians in Economics
Economists use Jacobians to analyze complex economic models and systems.
-
Input-Output Models
Jacobians help describe how changes in one sector of the economy affect others in input-output models. -
Optimization
In optimization problems, Jacobians are used to find the best solutions by analyzing the gradients of objective functions. -
Game Theory
Jacobians help analyze strategic interactions in game theory by studying how players' strategies affect outcomes.
Computational Aspects
Computing Jacobians efficiently is crucial for various applications, from scientific computing to machine learning.
-
Automatic Differentiation
Automatic differentiation techniques use Jacobians to compute derivatives efficiently, essential for training neural networks. -
Finite Element Analysis
In finite element analysis, Jacobians help transform local element coordinates to global coordinates, simplifying calculations. -
Numerical Methods
Jacobians are used in numerical methods to solve systems of nonlinear equations and optimize functions.
Historical Context
Understanding the historical context of Jacobians provides insight into their development and significance.
-
19th Century Development
Jacobians were developed in the 19th century as part of the broader study of determinants and matrix theory. -
Influence on Modern Mathematics
The development of Jacobians influenced modern mathematics, particularly in the fields of linear algebra and differential equations. -
Pioneers in the Field
Besides Carl Jacobi, other mathematicians like Augustin-Louis Cauchy and James Clerk Maxwell contributed to the development of Jacobians.
Fun Facts
Here are some fun and lesser-known facts about Jacobians.
-
Used in Video Games
Jacobians are used in video game physics engines to simulate realistic movements and interactions. -
Space Missions
NASA uses Jacobians in space missions to calculate trajectories and ensure accurate navigation.
The Final Word on Jacobians
Jacobians might sound complex, but they’re super useful in math and engineering. They help us understand how functions change and interact. From robotics to computer graphics, Jacobians play a big role in making things work smoothly. They’re not just for math geeks; anyone interested in how things move and change can benefit from knowing about them.
Understanding Jacobians can open doors to new ways of thinking and problem-solving. Whether you’re a student, a professional, or just curious, diving into the world of Jacobians can be rewarding. They’re a key tool in many fields, making complex problems easier to handle.
So, next time you see a robot moving or a computer game running smoothly, remember the Jacobians working behind the scenes. They’re more than just numbers; they’re the magic that makes things happen.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
