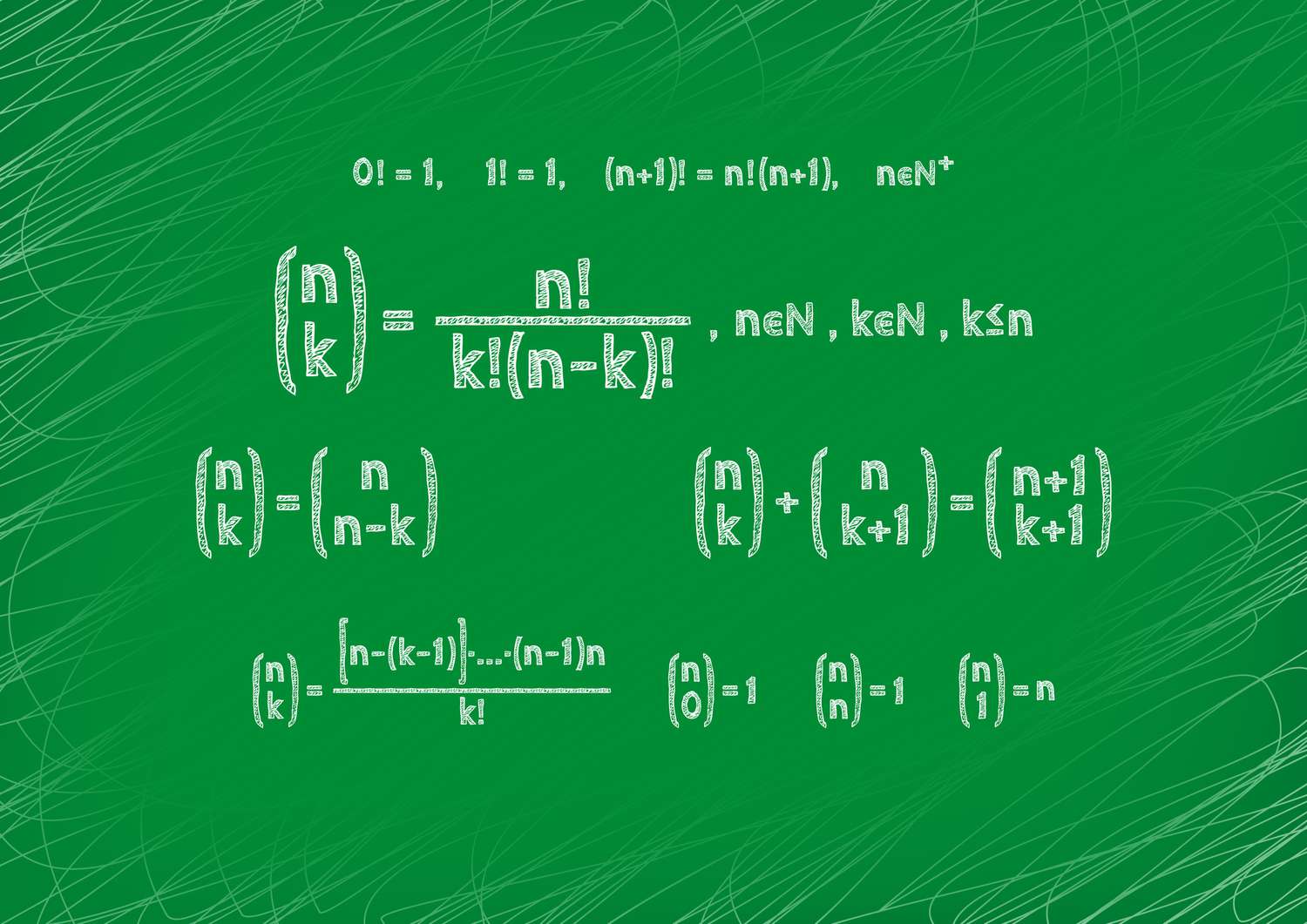
What is a factorial? A factorial, symbolized by an exclamation mark (!), is the product of all positive integers up to a given number. For example, 5! equals 5 × 4 × 3 × 2 × 1, which is 120. Factorials are fundamental in mathematics, especially in permutations, combinations, and probability. They help solve problems involving arrangements and sequences. Factorials grow incredibly fast; even 10! equals a whopping 3,628,800! Understanding factorials can make complex math problems simpler and more manageable. Ready to dive into the world of factorials? Let's explore 34 fascinating facts about this mathematical marvel!
What is Factorial?
Factorials are a fundamental concept in mathematics, often represented by an exclamation mark (!). They play a crucial role in various fields, including algebra, calculus, and computer science. Let's dive into some fascinating facts about factorials.
-
The factorial of a non-negative integer ( n ) is the product of all positive integers less than or equal to ( n ). For example, ( 5! = 5 times 4 times 3 times 2 times 1 = 120 ).
-
The factorial of zero is 1. This might seem strange, but ( 0! = 1 ) by definition, which helps in simplifying many mathematical expressions.
-
Factorials grow incredibly fast. For instance, ( 10! = 3,628,800 ), while ( 20! ) is a 19-digit number: 2,432,902,008,176,640,000.
Historical Background
Understanding the history of factorials can provide insight into their importance and development over time.
-
The concept of factorials dates back to ancient Indian mathematicians. They used it in permutations and combinations as early as the 12th century.
-
The notation ( n! ) was introduced by Christian Kramp in 1808. Before this, factorials were written out in long form, making calculations cumbersome.
-
Factorials were initially studied in the context of combinatorics, particularly in counting arrangements and permutations.
Applications in Mathematics
Factorials are not just theoretical; they have practical applications in various branches of mathematics.
-
In combinatorics, factorials are used to calculate permutations. For example, the number of ways to arrange ( n ) distinct objects is ( n! ).
-
Factorials are essential in binomial coefficients, which are used in binomial expansions. The binomial coefficient ( binom{n}{k} ) is calculated as ( frac{n!}{k!(n-k)!} ).
-
Factorials appear in calculus, particularly in the Taylor series expansion of functions. The general term of the Taylor series involves ( n! ) in the denominator.
Factorials in Computer Science
Factorials also have significant applications in computer science, especially in algorithms and data structures.
-
Recursive algorithms often use factorials as a classic example. A simple recursive function to compute ( n! ) calls itself with ( n-1 ) until it reaches 1.
-
Factorials are used in sorting algorithms, particularly in generating permutations. Heap's algorithm, for instance, generates all possible permutations of a given list.
-
In complexity theory, factorials help in understanding the growth rates of algorithms. They provide a benchmark for comparing the efficiency of different algorithms.
Interesting Properties
Factorials have some unique and interesting properties that make them a fascinating topic of study.
-
Stirling's approximation provides an approximate value for large factorials. It states that ( n! approx sqrt{2pi n} left(frac{n}{e}right)^n ).
-
Factorials are closely related to the Gamma function, which generalizes the factorial to non-integer values. For positive integers, ( Gamma(n) = (n-1)! ).
-
Factorials can be used to solve Diophantine equations, which are polynomial equations with integer solutions.
Fun Facts
Factorials can be fun and surprising in many ways. Here are some quirky facts about them.
-
The sum of the reciprocals of all factorials converges to a constant known as the Euler-Mascheroni constant, approximately 0.57721.
-
Factorions are numbers that equal the sum of the factorials of their digits. For example, 145 is a factorion because ( 1! + 4! + 5! = 145 ).
-
Factorials can be used to create magic squares, where the sum of numbers in each row, column, and diagonal is the same.
Factorials in Probability
Factorials play a significant role in probability theory, helping to calculate various probabilities and distributions.
-
Factorials are used in calculating probabilities in permutations and combinations. For example, the probability of drawing a specific hand in poker involves factorials.
-
The Poisson distribution, which models the number of events occurring within a fixed interval, uses factorials in its probability mass function.
-
Factorials are essential in the multinomial distribution, which generalizes the binomial distribution to more than two outcomes.
Factorials in Real Life
Factorials are not just confined to textbooks; they have real-life applications too.
-
Factorials are used in scheduling problems, such as determining the number of ways to schedule tasks or events.
-
In genetics, factorials help in calculating the number of possible genetic combinations.
-
Factorials are used in cryptography, particularly in generating keys and codes.
Factorials in Art and Music
Believe it or not, factorials have found their way into art and music as well.
-
Factorials are used in creating fractals, which are complex geometric shapes that can be split into parts, each of which is a reduced-scale copy of the whole.
-
In music theory, factorials help in understanding the permutations of notes and rhythms.
-
Factorials are used in algorithmic composition, where music is generated using mathematical algorithms.
Factorials in Puzzles and Games
Factorials make puzzles and games more challenging and interesting.
-
Sudoku puzzles often use factorials to determine the number of possible solutions.
-
Factorials are used in Rubik's Cube algorithms to calculate the number of possible configurations.
-
In chess, factorials help in calculating the number of possible moves and positions.
Factorials in Science
Factorials have applications in various scientific fields, including physics and chemistry.
-
In physics, factorials are used in statistical mechanics to calculate the number of possible microstates of a system.
-
Factorials are used in quantum mechanics, particularly in the calculation of wave functions and probabilities.
-
In chemistry, factorials help in understanding reaction rates and the number of possible products in a chemical reaction.
Factorials in Finance
Factorials also have applications in finance, particularly in risk management and investment strategies.
- Factorials are used in calculating the number of possible outcomes in financial models, such as option pricing and portfolio optimization.
The Final Countdown
Factorials might seem like just another math concept, but they’re everywhere. From combinatorics to probability, they play a huge role in solving complex problems. They even pop up in computer algorithms and statistical models. Knowing how to calculate and use them can give you an edge in understanding more advanced topics.
Remember, the factorial of a number is the product of all positive integers up to that number. It’s denoted by an exclamation mark, like 5!. This simple yet powerful tool can help you tackle a variety of challenges.
So next time you see a factorial, don’t just brush it off. Think about how it connects to the bigger picture. Whether you’re a student, a teacher, or just a curious mind, understanding factorials can open up new doors in your learning journey. Keep exploring, keep questioning, and most importantly, keep learning.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
