40 Facts About Basis Theory

What is Basis Theory?

Basis Theory is a fundamental concept in linear algebra and vector spaces. It helps us understand how vectors can be represented and manipulated. Here are some interesting facts about Basis Theory:

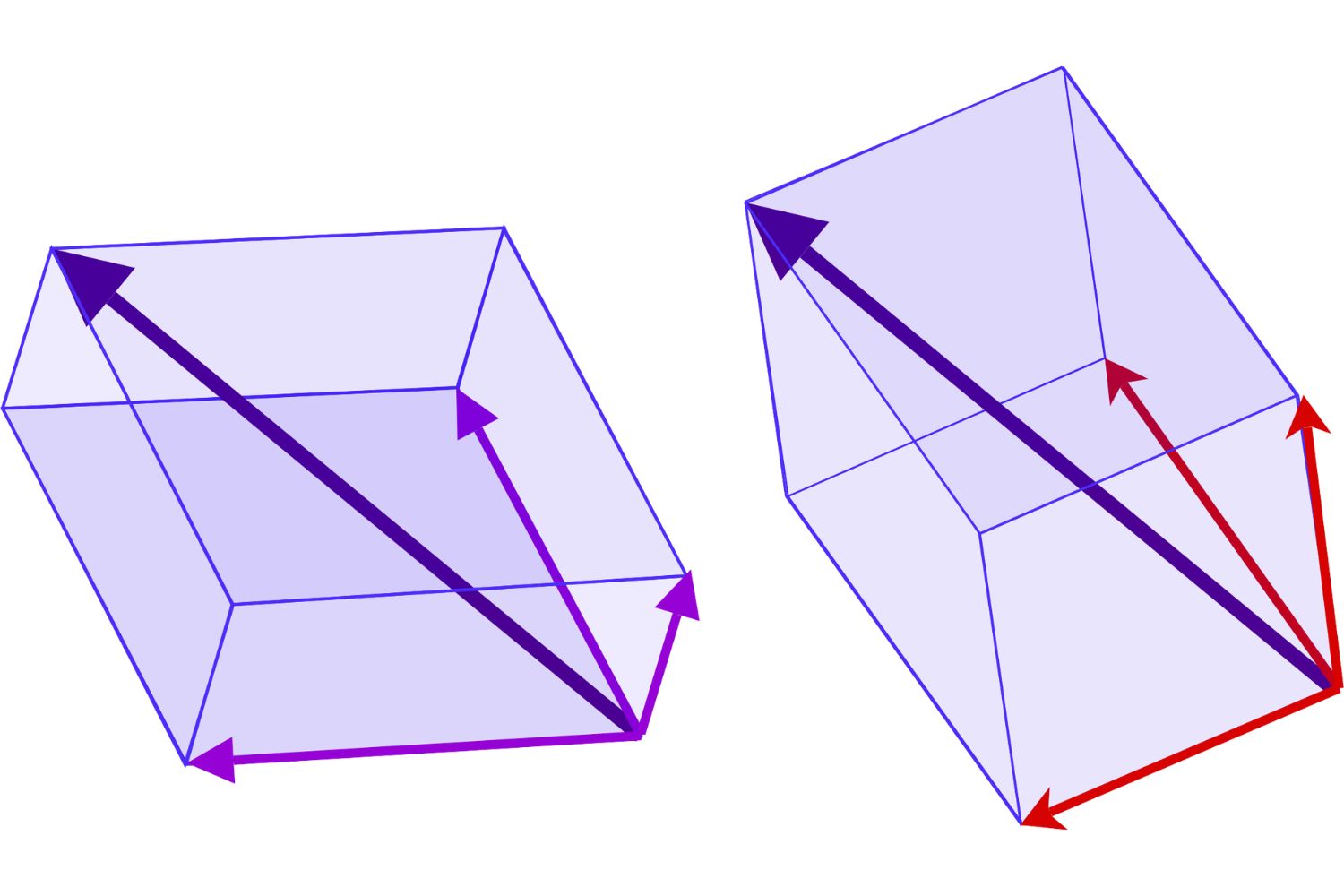
1. Basis Definition: A basis of a vector space is a set of vectors that are linearly independent and span the entire space.

2. Unique Representation: Every vector in a vector space can be uniquely represented as a linear combination of basis vectors.

3. Minimum Set: The basis is the smallest set of vectors needed to span the vector space.

4. Dimension: The number of vectors in a basis is called the dimension of the vector space.

5. Standard Basis: In Euclidean space, the standard basis consists of unit vectors along each axis.

6. Change of Basis: Vectors can be transformed from one basis to another using a change of basis matrix.

7. Orthonormal Basis: An orthonormal basis consists of vectors that are both orthogonal and normalized.

8. Gram-Schmidt Process: This process converts any basis into an orthonormal basis.

9. Eigenbasis: A basis formed by the eigenvectors of a matrix is called an eigenbasis.

10. Coordinate System: A basis provides a coordinate system for the vector space.

Applications of Basis Theory

Basis Theory isn't just a theoretical concept; it has practical applications in various fields. Let's explore some of these applications:

11. Computer Graphics: Basis vectors are used to represent 3D objects and transformations.

12. Quantum Mechanics: States of quantum systems are represented using basis vectors in Hilbert spaces.

13. Data Compression: Techniques like Principal Component Analysis (PCA) use basis vectors to reduce data dimensions.

14. Signal Processing: Fourier transforms use basis functions to analyze signals.

15. Robotics: Basis vectors help in defining the movement and orientation of robots.

16. Economics: Basis Theory is used in econometrics for modeling and analysis.

17. Cryptography: Lattice-based cryptography relies on basis vectors for security.

18. Machine Learning: Feature spaces in machine learning models are defined using basis vectors.

19. Control Systems: State-space representation of control systems uses basis vectors.

20. Image Processing: Basis functions are used in techniques like wavelet transforms for image compression and enhancement.

Historical Background of Basis Theory

Understanding the history of Basis Theory can provide context to its development and significance. Here are some historical facts:

21. Early Concepts: The idea of a basis can be traced back to the work of mathematicians like Euler and Lagrange.

22. Formal Definition: The formal definition of a basis was introduced by Giuseppe Peano in the late 19th century.

23. Vector Spaces: The concept of vector spaces and bases was further developed by Hermann Grassmann.

24. Linear Independence: The notion of linear independence, crucial to Basis Theory, was explored by Augustin-Louis Cauchy.

25. Modern Development: Basis Theory was rigorously formalized in the 20th century by mathematicians like David Hilbert and John von Neumann.

26. Applications in Physics: Basis Theory found applications in quantum mechanics through the work of Paul Dirac.

27. Computational Methods: The development of computational methods in the mid-20th century expanded the practical use of Basis Theory.

28. Educational Impact: Basis Theory is now a fundamental part of the curriculum in mathematics and engineering courses worldwide.

29. Nobel Prize: Some applications of Basis Theory in quantum mechanics contributed to Nobel Prize-winning research.

30. Interdisciplinary Influence: Basis Theory has influenced various fields, including computer science, economics, and engineering.

Fun and Surprising Facts about Basis Theory

Basis Theory can be fascinating and sometimes surprising. Here are some fun facts:

31. Infinite Dimensions: Some vector spaces, like function spaces, can have an infinite number of dimensions.

32. Fractals: Basis Theory helps in understanding the structure of fractals.

33. Music: Basis vectors can be used to analyze musical compositions and sounds.

34. Art: Artists use basis vectors to create and manipulate digital art.

35. Nature: Basis Theory can describe natural phenomena like wave patterns and crystal structures.

36. Games: Video game physics engines use basis vectors for realistic simulations.

37. Space Exploration: Basis Theory aids in the navigation and control of spacecraft.

38. Artificial Intelligence: AI algorithms use basis vectors for pattern recognition and data analysis.

39. Virtual Reality: Basis vectors help in creating immersive virtual reality experiences.

40. Sports Analytics: Basis Theory is used to analyze and improve athletic performance through data modeling.

Final Thoughts on Basis Theory

Basis Theory offers a fascinating glimpse into the world of mathematics and its applications. From its roots in linear algebra to its impact on computer science, this concept is more than just numbers and equations. It helps us understand complex systems, optimize processes, and even solve real-world problems. Whether you're a student, a professional, or just someone curious about how things work, knowing a bit about Basis Theory can be incredibly rewarding. It’s not just about abstract ideas; it’s about seeing the connections and patterns that shape our world. So next time you encounter a complex problem, remember that Basis Theory might just hold the key to unlocking a solution. Keep exploring, keep questioning, and who knows? You might discover something amazing.