Fourier Analysis might sound like a complex mathematical concept, but it's actually a powerful tool used in many fields, from engineering to music. Ever wondered how your favorite songs get compressed into MP3 files or how MRI machines create detailed images of your brain? Fourier Analysis is the magic behind these technologies. By breaking down complex signals into simpler components, it helps us understand and manipulate data in ways that would otherwise be impossible. Whether you're a student, a tech enthusiast, or just curious, these 39 facts will give you a clearer picture of why Fourier Analysis is so important. Buckle up for a journey through the fascinating world of waves, frequencies, and transformations!
Key Takeaways:
- Fourier Analysis breaks down complex functions into simpler components using sine and cosine terms. It's used in engineering, physics, and mathematics to solve problems and understand the world around us.
- From analyzing music and restoring art to predicting earthquakes and studying stock market trends, Fourier Analysis has diverse and fascinating applications. However, it also faces challenges with non-stationary signals and computational complexity.
What is Fourier Analysis?
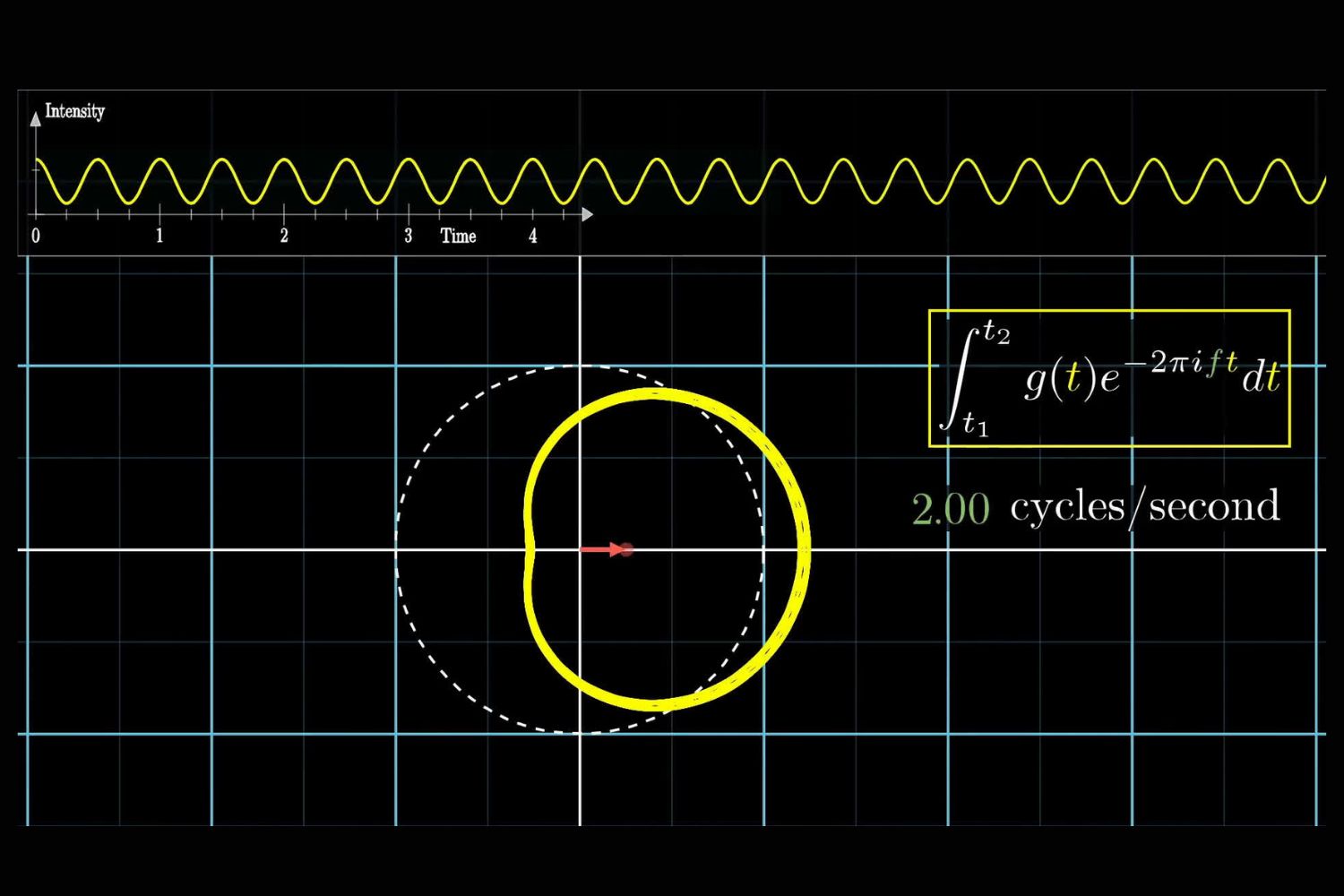
Fourier Analysis is a mathematical method used to break down complex functions into simpler components. This technique is widely used in various fields, including engineering, physics, and signal processing. Let's dive into some fascinating facts about Fourier Analysis.
-
Named After Joseph Fourier: The method is named after French mathematician Joseph Fourier, who introduced the concept in the early 19th century.
-
Decomposes Functions: Fourier Analysis decomposes a function into a sum of sine and cosine terms, making it easier to analyze.
-
Fourier Series: The Fourier Series represents periodic functions as a sum of sine and cosine functions.
-
Fourier Transform: The Fourier Transform extends the Fourier Series to non-periodic functions, converting them from the time domain to the frequency domain.
-
Inverse Fourier Transform: This process converts a function back from the frequency domain to the time domain.
Applications in Engineering
Fourier Analysis has numerous applications in engineering, from signal processing to system design. Here are some key facts about its engineering applications.
-
Signal Processing: It's used to analyze and filter signals, removing noise and enhancing important features.
-
Image Compression: JPEG compression uses Fourier Analysis to reduce file sizes without significant loss of quality.
-
Audio Engineering: Fourier Analysis helps in equalizing sound frequencies and removing unwanted noise.
-
Electrical Engineering: It's used to design and analyze circuits, particularly in the study of alternating current (AC) signals.
-
Mechanical Vibrations: Engineers use it to study and control vibrations in mechanical systems.
Importance in Physics
Fourier Analysis plays a crucial role in understanding various physical phenomena. Here are some intriguing facts about its importance in physics.
-
Quantum Mechanics: It's used to solve the Schrödinger equation, which describes how quantum states evolve over time.
-
Heat Transfer: Fourier's Law of Heat Conduction is a fundamental principle in thermodynamics.
-
Wave Propagation: It helps in analyzing how waves propagate through different media.
-
Optics: Fourier Analysis is used in the study of light diffraction and interference patterns.
-
Astronomy: Astronomers use it to analyze the light spectra from stars and galaxies.
Role in Mathematics
In mathematics, Fourier Analysis is a powerful tool for solving differential equations and other complex problems. Here are some notable facts.
-
Partial Differential Equations: It's used to solve partial differential equations, which describe various physical systems.
-
Harmonic Analysis: This branch of mathematics studies the representation of functions as sums of basic waves.
-
Probability Theory: Fourier transforms are used in probability theory to study characteristic functions.
-
Number Theory: It's applied in number theory to study the distribution of prime numbers.
-
Functional Analysis: Fourier Analysis is a key concept in functional analysis, which studies spaces of functions.
Historical Development
The development of Fourier Analysis has a rich history, with contributions from many mathematicians. Here are some historical facts.
-
Joseph Fourier's Work: Fourier's 1822 book "The Analytical Theory of Heat" laid the foundation for Fourier Analysis.
-
Euler's Contributions: Leonhard Euler made early contributions to the theory of trigonometric series.
-
Dirichlet's Conditions: Johann Peter Gustav Lejeune Dirichlet formulated conditions under which a function can be represented by a Fourier series.
-
Riemann's Insights: Bernhard Riemann extended Fourier's ideas to more general functions.
-
Lebesgue Integration: Henri Lebesgue's work on integration theory provided a rigorous foundation for Fourier Analysis.
Modern Applications
Today, Fourier Analysis is used in a wide range of modern applications. Here are some fascinating facts about its contemporary uses.
-
Medical Imaging: MRI and CT scans use Fourier transforms to create detailed images of the human body.
-
Cryptography: It's used in cryptographic algorithms to secure digital communications.
-
Weather Forecasting: Meteorologists use it to analyze atmospheric data and predict weather patterns.
-
Economics: Economists use Fourier Analysis to study cyclical patterns in economic data.
-
Machine Learning: It's used in machine learning algorithms to process and analyze large datasets.
Fun Facts
Fourier Analysis isn't just for scientists and engineers; it has some fun and surprising aspects too. Here are some fun facts.
-
Music Analysis: Musicians use it to analyze and synthesize musical sounds.
-
Art Restoration: Art conservators use it to analyze and restore paintings.
-
Speech Recognition: It's used in speech recognition software to convert spoken words into text.
-
Seismology: Seismologists use it to analyze earthquake waves and predict future quakes.
-
Stock Market: Traders use it to analyze stock market trends and make investment decisions.
Challenges and Limitations
Despite its many uses, Fourier Analysis has some challenges and limitations. Here are some key facts.
-
Non-Stationary Signals: It struggles with non-stationary signals, which change over time.
-
Computational Complexity: The calculations can be computationally intensive, especially for large datasets.
-
Gibbs Phenomenon: This phenomenon causes overshoots near discontinuities in the function being analyzed.
-
Approximation Errors: The accuracy of the analysis depends on the number of terms used in the Fourier series or transform.
Fourier Analysis: A Fascinating World
Fourier Analysis isn't just for math geeks. It's a powerful tool used in everything from music to medical imaging. This method breaks down complex signals into simpler components, making it easier to analyze and understand. Whether you're tuning a guitar or diagnosing a heart condition, Fourier Analysis plays a crucial role.
Understanding its basics can open doors to new insights and applications. From its origins with Joseph Fourier to its modern-day uses, this mathematical marvel continues to impact our daily lives. So next time you listen to your favorite song or get an MRI scan, remember the math behind the magic. Fourier Analysis is more than just numbers; it's a bridge connecting theory with real-world solutions. Dive in, explore, and see how this fascinating field can change your perspective.
Frequently Asked Questions
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
