34 Facts About Hyperbolic Geometry

What is Hyperbolic Geometry?

Hyperbolic geometry is a fascinating branch of mathematics that explores the properties of spaces with constant negative curvature. Unlike the familiar Euclidean geometry, hyperbolic geometry offers a unique perspective on shapes, lines, and angles.

1. Hyperbolic geometry was first discovered by Nikolai Lobachevsky and János Bolyai independently in the early 19th century.
2. In hyperbolic geometry, the sum of the angles of a triangle is always less than 180 degrees.
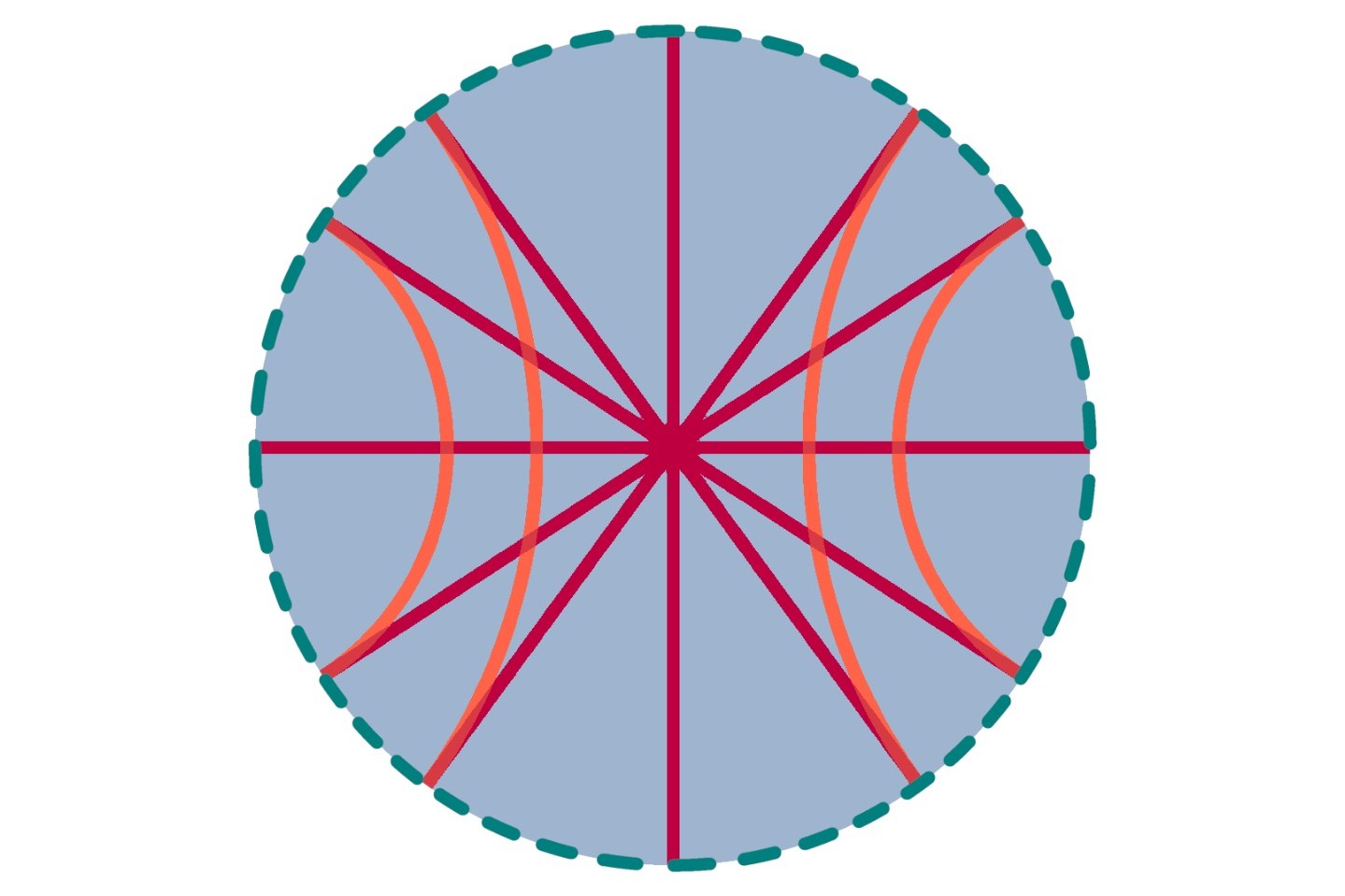
3. Parallel lines in hyperbolic geometry can diverge away from each other, unlike in Euclidean geometry where they remain equidistant.
4. The Poincaré disk model is a common way to visualize hyperbolic geometry, where the entire hyperbolic plane is represented inside a circle.
5. Hyperbolic geometry is used in the theory of special relativity to describe the geometry of spacetime.

Unique Properties of Hyperbolic Geometry

Hyperbolic geometry has several unique properties that set it apart from other types of geometry. These properties lead to interesting and sometimes counterintuitive results.

6. In hyperbolic geometry, there are infinitely many lines that can pass through a point and not intersect a given line.
7. Circles in hyperbolic geometry have a different relationship between their radius and circumference compared to Euclidean circles.
8. The area of a triangle in hyperbolic geometry is proportional to the deficit of its angle sum from 180 degrees.
9. Hyperbolic planes can be tiled with regular polygons in ways that are impossible in Euclidean geometry.
10. The concept of distance in hyperbolic geometry is different, with distances increasing exponentially as you move away from a point.

Applications of Hyperbolic Geometry

Hyperbolic geometry isn't just a theoretical curiosity; it has practical applications in various fields, including physics, computer science, and art.

11. Hyperbolic geometry is used in the design of certain types of networks, such as the internet, to optimize data routing.
12. In art, hyperbolic geometry has inspired many works, including the famous "Circle Limit" series by M.C. Escher.
13. The study of hyperbolic geometry has led to advances in understanding the shape and structure of the universe.
14. Hyperbolic geometry is used in the field of complex analysis, particularly in the study of Riemann surfaces.
15. The principles of hyperbolic geometry are applied in the design of certain types of optical systems.

Historical Development of Hyperbolic Geometry

The development of hyperbolic geometry was a significant milestone in the history of mathematics, challenging long-held assumptions and opening up new areas of study.

16. Before the discovery of hyperbolic geometry, Euclidean geometry was considered the only possible geometry.
17. The discovery of hyperbolic geometry showed that the parallel postulate of Euclidean geometry is not a necessary truth.
18. Gauss, one of the greatest mathematicians, also worked on hyperbolic geometry but did not publish his findings.
19. The development of hyperbolic geometry led to the creation of non-Euclidean geometries, expanding the scope of mathematical research.
20. Hyperbolic geometry played a crucial role in the development of modern geometry and topology.

Visualizing Hyperbolic Geometry

Visualizing hyperbolic geometry can be challenging due to its non-intuitive properties, but several models and tools help make it more accessible.

21. The Poincaré half-plane model is another way to represent hyperbolic geometry, using the upper half of the complex plane.
22. Hyperbolic tessellations, or tilings, are a popular way to visualize the properties of hyperbolic space.
23. Software tools like Hyperbolic Geometry Explorer allow users to interact with and explore hyperbolic spaces.
24. The Klein model represents hyperbolic geometry in a way that preserves straight lines but distorts angles.
25. Hyperbolic crochet is a craft technique that creates physical models of hyperbolic planes, making the concepts more tangible.

Challenges and Misconceptions

Despite its many fascinating properties, hyperbolic geometry is often misunderstood or overlooked. Addressing these challenges can help more people appreciate its beauty and importance.

26. One common misconception is that hyperbolic geometry is purely theoretical and has no practical applications.
27. Some people mistakenly believe that hyperbolic geometry contradicts Euclidean geometry, rather than complementing it.
28. The abstract nature of hyperbolic geometry can make it difficult for students to grasp without proper visualization tools.
29. There is a misconception that hyperbolic geometry is only relevant to mathematicians, when in fact it has applications in many fields.
30. Understanding hyperbolic geometry requires a shift in thinking, as many of its properties are counterintuitive compared to Euclidean geometry.

Future Directions in Hyperbolic Geometry

The study of hyperbolic geometry continues to evolve, with new discoveries and applications emerging regularly. These future directions promise to further expand our understanding of this intriguing field.

31. Researchers are exploring the connections between hyperbolic geometry and quantum computing.
32. Advances in virtual reality technology are providing new ways to visualize and interact with hyperbolic spaces.
33. The study of hyperbolic geometry is contributing to new insights in the field of cosmology.
34. Ongoing research is investigating the potential applications of hyperbolic geometry in materials science and engineering.

Hyperbolic Geometry: A World of Wonders

Hyperbolic geometry isn't just a bunch of fancy math terms. It’s a whole new way to look at shapes, spaces, and the universe. From the way parallel lines behave to the unique properties of triangles, this branch of geometry breaks all the rules we learned in school. It’s got real-world applications too, like in navigation systems and even in the way we understand the cosmos.

Understanding hyperbolic geometry can open up a new perspective on how we see the world around us. It’s not just for mathematicians; anyone curious about the universe can appreciate its beauty and complexity. So next time you hear about hyperbolic geometry, remember it’s more than just numbers and equations. It’s a fascinating journey into the unknown, showing us that there’s always more to learn and explore.