28 Facts About Analytic Continuation

What is Analytic Continuation?

Analytic continuation is a method in complex analysis used to extend the domain of a given analytic function. This technique allows mathematicians to define functions beyond their initial boundaries.

1. 01Analytic continuation helps extend the domain of functions beyond their original limits.
2. 02It is a powerful tool in complex analysis, a branch of mathematics dealing with complex numbers and functions of complex variables.
3. 03The process involves finding a new function that matches the original function within its initial domain but extends beyond it.

Historical Background

Understanding the history of analytic continuation provides context for its development and importance.

4. 04The concept dates back to the 19th century, with significant contributions from mathematicians like Bernhard Riemann.
5. 05Riemann used analytic continuation to study Riemann surfaces, which are complex structures that help visualize multi-valued functions.
6. 06Karl Weierstrass also played a crucial role by formalizing the theory of analytic continuation and developing related concepts.

Applications in Mathematics

Analytic continuation has numerous applications across various fields of mathematics.

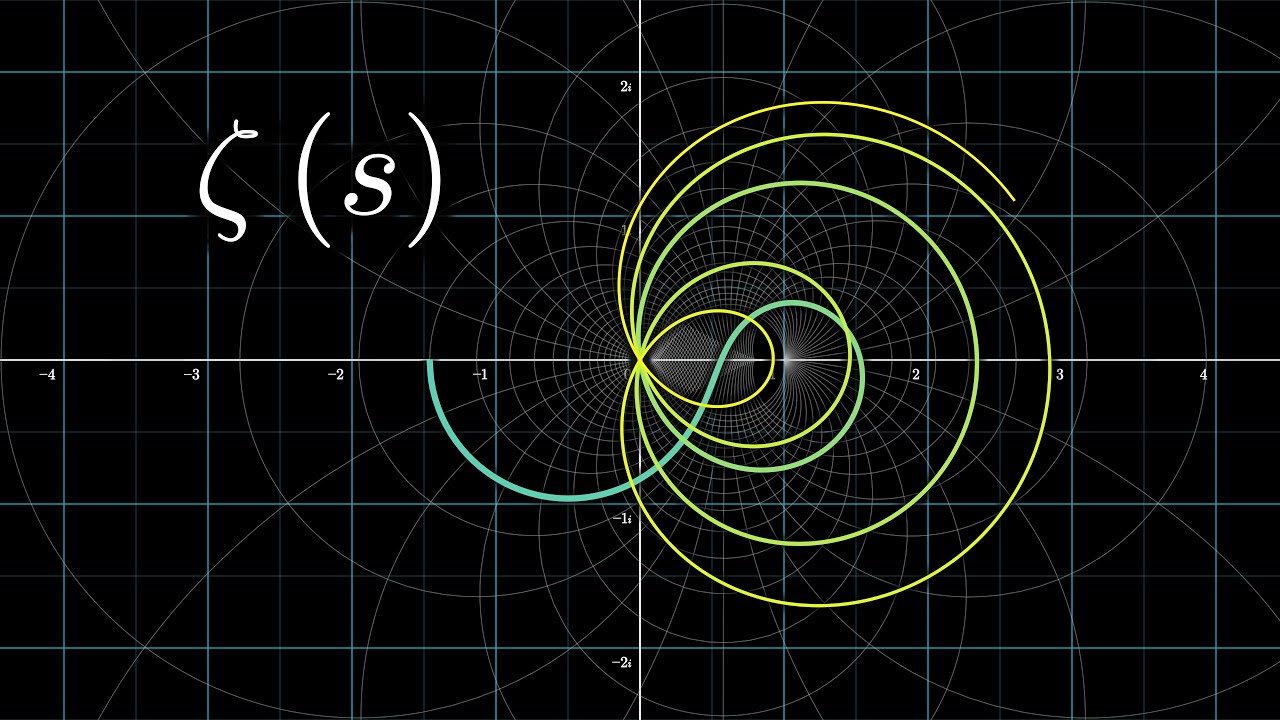
7. 07It is used in number theory to study properties of functions like the Riemann zeta function.
8. 08In differential equations, analytic continuation helps find solutions that extend beyond the initial conditions.
9. 09Quantum mechanics employs analytic continuation to solve problems related to wave functions and energy levels.

Techniques and Methods

Several techniques are used to achieve analytic continuation, each with its own advantages and limitations.

10. 10Power series expansion is a common method, where a function is expressed as an infinite sum of terms.
11. 11Schwarz reflection principle is another technique, which uses symmetry properties of functions to extend their domain.
12. 12Monodromy theorem helps in understanding how functions behave when analytically continued along different paths.

Challenges and Limitations

Despite its usefulness, analytic continuation comes with its own set of challenges.

13. 13Finding a suitable function for continuation is not always straightforward and may require complex calculations.
14. 14Singularities, or points where a function becomes undefined, can pose significant obstacles.
15. 15The process may lead to multi-valued functions, which require careful handling to avoid inconsistencies.

Real-World Examples

Analytic continuation isn't just a theoretical concept; it has practical applications in various fields.

16. 16In engineering, it helps in signal processing by extending the frequency domain of signals.
17. 17Economics uses analytic continuation to model and predict market behaviors over extended periods.
18. 18In physics, it aids in the study of phase transitions and critical phenomena.

Famous Problems and Solutions

Several famous mathematical problems have been solved using analytic continuation.

19. 19The Riemann Hypothesis, one of the most famous unsolved problems in mathematics, involves the analytic continuation of the Riemann zeta function.
20. 20Dirichlet's problem in potential theory uses analytic continuation to find harmonic functions that satisfy specific boundary conditions.
21. 21Picard's theorem relies on analytic continuation to describe the behavior of entire functions.

Modern Developments

Recent advancements have expanded the scope and applications of analytic continuation.

22. 22Computer algorithms now assist in performing complex analytic continuations, making the process faster and more accurate.
23. 23Machine learning techniques are being explored to predict and extend functions in innovative ways.
24. 24Interdisciplinary research combines analytic continuation with fields like biology and chemistry to solve complex problems.

Fun Facts

Analytic continuation has some interesting and lesser-known aspects that make it a fascinating topic.

25. 25The concept is closely related to fractals, which are complex geometric shapes that can be split into parts, each of which is a reduced-scale copy of the whole.
26. 26Mandelbrot set, a famous fractal, is studied using techniques from analytic continuation.
27. 27Euler's formula, which connects complex exponentials to trigonometric functions, can be extended using analytic continuation.
28. 28The Gamma function, an extension of the factorial function to complex numbers, is another example of a function extended through analytic continuation.

Final Thoughts on Analytic Continuation

Analytic continuation isn't just a fancy term; it's a powerful tool in mathematics. It helps extend the domain of functions, making complex problems simpler. This technique plays a crucial role in various fields like physics, engineering, and even number theory. By understanding it, you're not just learning math; you're unlocking new ways to solve problems.

Remember, the key idea is to extend a function beyond its original limits while keeping its properties intact. This concept has been around for centuries, proving its timeless value. Whether you're a student, a professional, or just curious, grasping analytic continuation can open doors to deeper mathematical understanding.

So, next time you encounter a complex function, think about how analytic continuation might help. It's a small step with a big impact, making the impossible possible. Keep exploring, keep questioning, and most importantly, keep learning.